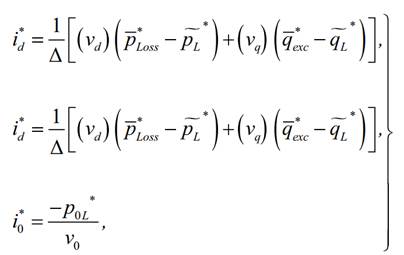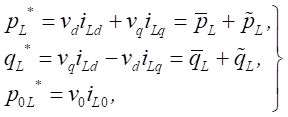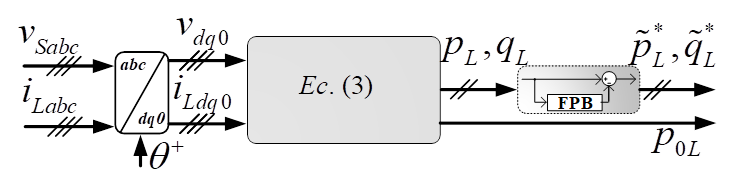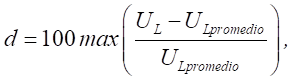Vol. 5 N°2, julio-diciembre 2024, pág. 41-53

ISSN 2618-5520 online - ISSN 2683-7021 impresa

DOI: https://doi.org/10.36995/j.masingenio.2024.05.02.004

Sistema de Excitación y Compensación para Generadores de Inducción basado en la Teoría de Potencia Instantánea

Aldo Javier Benítez ^{a, *} (https://orcid.org/0000-0002-6927-3037), Rubén Orlando Núñez ^{a, b} (https://orcid.org/0000-0002-8319-727X), Pablo de la Barrera ^c (https://orcid.org/0000-0003-4944-9522), Guillermo Oscar García ^c (https://orcid.org/0000-0002-4652-8893)

^a Universidad Nacional de Misiones (UNaM). Facultad de Ingeniería, Grupo de Investigación y Desarrollo en Electrónica (GIDE). Oberá, Misiones, Argentina.

^b Instituto de Materiales de Misiones (IMAM)–CONICET, Argentina.

^c Universidad Nacional de Río Cuarto (UNRC). Grupo de Electrónica Aplicada (GEA)–CONICET. Río Cuarto, Córdoba, Argentina.

e-mails: javierbenitez@fio.unam.edu.ar, ruben.nunez@fio.unam.edu.ar, pmdelabarrera@gmail.com, ggarciasapino@gmail.com

Resumen

Se reporta la aplicación de la Teoría de Potencia Instantánea a un sistema de generación autónomo trifásico, capaz de alimentar cargas desequilibradas monofásicas y/o trifásicas lineales. Este sistema propuesto se basa en el uso de un motor de inducción (MI) del tipo jaula de ardilla, un sistema de excitación compuesto por un banco de capacitores y un convertidor CC-AC de cuatro piernas que actúa como una fuente de corriente, todos conectados en paralelo, formando lo que llamamos Generador de Inducción (GI). Con esta propuesta es posible extraer corrientes sinusoidales y equilibradas del MI, reduciendo así las perdidas y las fluctuaciones de torque en la maquina; características indeseables que aparecen cuando se alimentan cargas trifásicas desequilibradas. Además, con el uso de un MI tipo jaula de ardilla, el sistema de generación tiene un bajo costo, una robustez adecuada y una mínima necesidad de mantenimiento. Se presentan resultados experimentales y de simulación que validan la viabilidad práctica de la propuesta.

Palabras Clave – Generador de inducción, regulación de voltaje, cargas desequilibradas, convertidores de cuatro piernas, teoría de potencia instantánea.

Abstract

The application of the Instant Power Theory to an autonomous three−phase generation system, capable of feeding unbalanced single−phase and/or three−phase linear loads, is reported. This proposed system is based on the use of an induction motor (IM) of the squirrel cage type, an excitation system composed of a capacitor bank and a four−leg CC−AC converter that acts as a current source, all connected in parallel and forming what we call Induction Generator (IG). With this proposal it is possible to extract sinusoidal and balanced currents from the IM, thereby reducing losses and torque fluctuations in the machine; undesirable characteristics that appear when three−phase unbalanced loads are fed, in addition, with the use of a squirrel cage type IM, the generation system has low cost, adequate robustness and minimal need for maintenance. Experimental and simulation results are presented that validate the practical feasibility of the proposal.

Keywords – Induction generator, voltage regulation, unbalanced loads, four-leg converters, instantaneous power theory.

1. Introducción

La necesidad de acceder a la energía eléctrica en lugares remotos, donde no se tiene acceso a las redes eléctricas convencionales ni a servicios técnicos especializados para realizar mantenimiento y/o reparaciones, ha impulsado diferentes propuestas de sistemas de generaciones de energía eléctrica a partir de diferentes fuentes de energía renovables como las solares, eólicas, entre otras. En la mayoría de estos sistemas se requieren el uso de máquinas eléctricas rotativas [1]–[3], los cuales deben ser lo más robusto posible y de bajo mantenimiento [4].

Las máquinas de inducción (MI) tipo jaula de ardilla son las más utilizadas como motor en todo el mundo, son las más estandarizadas, son las más robustas, no poseen contactos móviles, requieren de un mínimo de mantenimiento y son las de menor costo debido a su simplicidad constructiva y gran escala de producción [5]–[8]. Estas características de la MI hacen que la misma sea atractiva para utilizarla como generador en lugares aislados de la red eléctrica convencional, con la desventaja de que en este modo de funcionamiento ésta requiere de un sistema de excitación no convencional para regular la tensión generada. En referencia a esto, se han propuesto diferentes alternativas para resolver esta cuestión, desde conectar un banco de capacitores en paralelo con la maquina [9], la opción más simple, hasta el uso de convertidores electrónicos de potencia con complejos algoritmos de control con el objetivo de brindar una mejor calidad de energía [4], [10], [11]. Al conjunto MI y sistema de excitación se lo denomina Generador de Inducción (GI).

Cuando los generadores alimentan cargas lineales, trifásicas equilibradas, las corrientes que circulan por el mismo son sinusoidales equilibradas, dando como resultado un funcionamiento “suave”. Por otro lado, cuando se alimentan cargas trifásicas desequilibradas, como por ejemplo un conjunto de cargas monofásicas diferentes entre ellas, pueden generarse corrientes de secuencia cero y negativa, lo que ocasiona calentamiento y par pulsante, logrando con ellos disminuciones en el rendimiento y en la vida útil del sistema [12]–[19].

Existen diferentes métodos propuestos para compensar el desequilibrio de cargas, los que utilizan componentes eléctricos pasivos, tales como bancos de capacitores e inductores, denominados compensadores pasivos y los que utilizan convertidores electrónicos, denominados compensadores activos. En relación con compensadores pasivos se han propuesto trabajos como los presentados en [20] y [21], en los cuales se presentan métodos de compensación de desequilibrios de cargas. La desventaja de ambas propuestas es que son diseñados para cargas constantes [22].

En relación con los compensadores activos se han publicado trabajos como los presentados en [23]–[26], que proponen sistemas de excitación para generadores de inducción (GI), con estos además de regular la tensión permiten compensar armónicos y desequilibrio de cargas, minimizando los inconvenientes asociados a estos últimos. En [23] se propone una topología compuesta por un GI y un convertidor en paralelo que permite alimentar cargas monofásicas no lineales, se compensan los armónicos. A pesar de que, tanto el generador como el convertidor son trifásicos la topología solo permite la alimentación de cargas monofásicas.

En [24] y [25] se propone un generador de inducción con regulación de tensión y frecuencia. Se utiliza un GI basado en una topología de excitación denominada hibrida, que consta de una MI conectada en paralelo con un banco de capacitores conmutados y un convertidor CC−CA de cuatro hilos. Se presentan resultados experimentales, en los cuales pueden observarse transitorios ocasionados por la conmutación del banco de capacitores.

También, se han publicado compensadores activos en los cuales se propone controlar a los GI utilizando la Teoría de Potencia Instantánea o Teoría p−q [27]–[29]. Algunas de estas propuestas pueden observarse en las referencias [30]–[33], en las cuales se presentan sistemas de generación trifásicas para alimentar cargas trifásicas equilibradas. En este trabajo se propone mostrar los avances en la implementación experimental de un sistema de generación trifásica de cuatro hilos, basado en la Teoría p−q para alimentar cargas monofásicas y trifásicas desequilibradas. Esta propuesta de generación posee un sistema de excitación para una MI compuesto por un banco de capacitores y un convertidor CC−CA de cuatro piernas que actúa como fuente de corriente, ambos conectados en paralelo con la máquina. Este trabajo está organizado de la siguiente manera: en la Sección 2 se describe el sistema de excitación y de compensación de desequilibrio propuesto, en las Secciones 3 y 4 se presentan resultados de simulación y experimentales, respectivamente, los cuales demuestran la viabilidad práctica de la propuesta. Finalmente, en la Sección 5 se presentan las conclusiones obtenidas.

2. Descripción del sistema propuesto

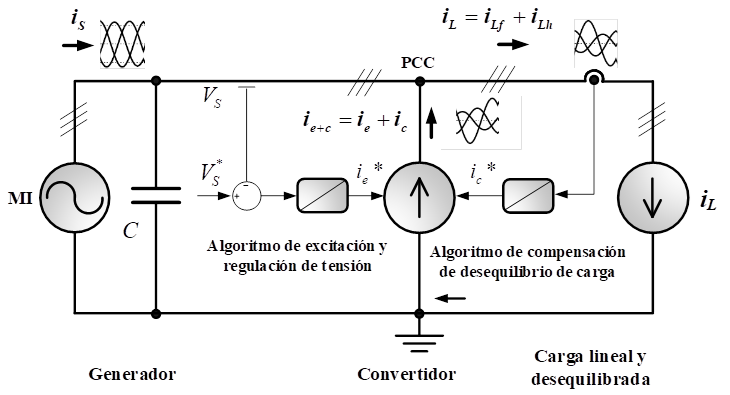
En la Fig. 1 se presenta un diagrama de bloques conceptual del sistema de excitación y compensación, propuesto, para implementarse en un sistema de generación eléctrica basado en una MI. En este diagrama la MI es representada por una fuente de tensión de CA trifásica ideal, con una tensión y corriente sinusoidal, V_S e i_S, respectivamente. La carga es representada por una fuente de corriente, i_L, la cual resulta de la suma de la componente fundamental, i_Lf, y de sus componentes armónicas, i_La. Además, puede apreciarse en esta figura, una representación del sistema de excitación utilizado para excitar al GI y regular la tensión en el Punto de Conexión Común (PCC), entre el generador y la carga. Este sistema está compuesto por un banco de capacitores (C) y por una fuente de corriente controlada, a su vez compuesta por un convertidor con lazo de control de corriente, la cual realiza una inyección de una componente de corriente reactiva i_e y de una componente de compensación de desequilibrio de carga, i_c, logrando con esto que la corriente que circula por la MI sea sinusoidal.

En la Fig. 1 también se representan dos lazos de control, los cuales están asociados a los cálculos de las referencias de las componentes de corriente de excitación  y de compensación, . Estos cálculos son realizados mediante algoritmos basados en la teoría de potencia instantánea o p−q [27], [28].

2.1. Algoritmo de excitación y de compensación de desequilibrio de carga

El algoritmo de control de este convertidor tiene como objetivo la inyección de una corriente, en el PCC, compuesta por la suma de dos componentes, una reactiva y otra de compensación de desequilibrio de carga. Con la inyección de estas componentes se logra que las corrientes que circulan por la MI sean sinusoidales y equilibradas, que las tensiones generadas estén reguladas y que la corriente del conductor de neutro sea minimizada.

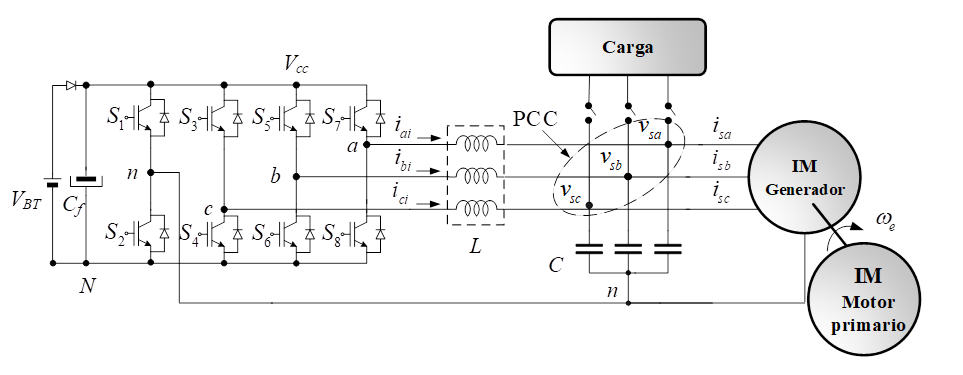
En la Fig. 2 se representa al prototipo experimental implementado. En esta figura se representa al sistema de excitación, a la fuente de corriente, el GI y a la carga. La fuente de corriente está implementada con un convertidor CC-CA de cuatro piernas, el cual posee un lazo interno de control de corrientes, el cual se basa en una referencia .

El GI está conectado a un motor impulsor primario, el cual emula por ejemplo una turbina hidráulica, que impone una velocidad  al eje de la MI, pudiendo variar en un determinado rango, en función a un regulador.

El algoritmo de control de corrientes calcula las referencias de corrientes, en base a la teoría p−q [34], utilizando un referencial en variables  sincrónico con la secuencia positiva de las tensiones generadas por el GI, la detección de secuencia positiva se implementa mediante un integrador generalizado de segundo orden [35]. Las expresiones de cálculo de las corrientes se muestran en el sistema de ecuaciones (1).

Fig. 1. Diagrama conceptual del sistema de generación eléctrica propuesto.

Fig. 2. Circuito simplificado del prototipo experimental implementado.

(1)

donde v_d, v_q y v₀ representan las tensiones del generador (v_Sabc) en el referencial d_q0 y Δ y puede calcularse a partir de (2).

(2)

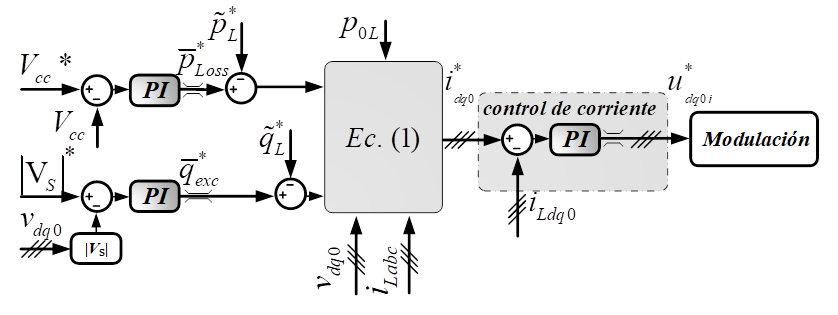
En la Fig. 3 se representa un diagrama de bloques correspondiente al algoritmo de excitación y regulación de tensión, el cual tiene como objetivo calcular las referencias  de la fuente de corriente, cuyas referencias provienen de:

o el lazo de regulación de la tensión de la barra de CC de la fuente de corriente, V_cc, cuya referencia es ;

o el lazo de regulación de la tensión generada, , cuya referencia es ;

o el algoritmo de compensación de desequilibrio de carga, basado en la medición de las tensiones y corrientes sobre la misma.

o

Fig. 3. Diagrama de bloques del algoritmo de excitación y de regulación de tensión en la barra de CC.

Inicialmente para que la maquina genere energía es necesario que el convertidor provea una corriente reactiva inicial, para lo cual en este caso se utiliza una batería de 24 V conectada a la barra de CC, que junto con la corriente provista por los capacitores darán inicio al proceso de autoexcitación del GI. Una vez que el GI aumenta su tensión inicial y logra valores nominales de tensión, la batería de 24 V ya no se utiliza. Existe un intercambio de potencia activa y reactiva entre la barra de CA y CC, durante el arranque y funcionamiento del GI que está controlado por los lazos de control.

El lazo de control de la tensión V_cc calcula la referencia de la potencia activa media, , que la fuente de corriente debe transferir desde su barra de CC hacia la de CA del GI para compensar la pérdida de potencia de la fuente de corriente, utilizada para regular la tensión en la barra de CC.

El lazo de control del módulo del vector tensión trifásica, |V_S|, calcula la referencia de potencia reactiva media, , que la fuente de corriente debe transferir desde su barra de CC hacia la de CA para excitar a la MI y regular la tensión generada.

En la Fig. 4 se representa, en diagramas de bloques, el algoritmo de compensación de desequilibrio de carga, utilizado para calcular los valores de las potencias instantáneas, ,  y , determinadas a partir del sistema de ecuaciones (3).

(3)

donde i_Ld, i_Lq e i_L0 representan las corrientes en la carga en el referencial d_q0. A su vez, estas componentes de potencia instantáneas pueden descomponerse en sus partes continuas y oscilatorias, ,  respectivamente, mediante un filtro pasa bajos (FPB) del tipo recursivo [36], como se representa en la figura.

Las componentes de potencias que se desean compensar son las oscilatorias, debido a que provocan desequilibrio de tensiones y corrientes [28]. También se desea compensar la componente de secuencia cero (p_0L), debido a que indica circulación de corriente por el neutro, lo cual no es conveniente debido a la generación de pérdidas de potencia y desvío de la tensión del neutro.

Una vez obtenidas las potencias , ingresan al bloque dado por el sistema de ecuaciones (1), de la Fig. 3, para el cálculo de las referencias de corriente , que la fuente de corriente debe inyectar en la barra de CA.

Fig. 4. Diagrama de bloques del algoritmo de compensación de desequilibrio de carga, basado en la teoría p−q.

2.2. Descripción Modelo y Control del GI

Para obtener el modelo del sistema de generación se hicieron las siguientes simplificaciones: El GI es considerado como una fuente de tensión alterna ideal, con tensiones equilibradas y que su régimen de funcionamiento es constante; que el convertidor utilizado es uno de CC−CA trifásico de cuatro piernas con un filtro LC a la salida, el cual tiene en cuenta el banco de capacitores necesario para la autoexcitación; que la barra de CC es una fuente de tensión constante ideal; que los inductores del filtro poseen valores iguales y constantes en cada fase.

A partir del modelo obtenido en el dominio frecuencial se determinaron los valores de los parámetros de cada compensador Proporcional Integral (PI) representado en la Fig. 3; considerando características de desempeño transitorio y de régimen permanente establecidas a partir de las limitaciones de los máximos valores de desequilibrios de tensiones y corrientes, indicados en la Tabla 1. Para su implementación, en el Procesador Digital de Señales (DSP−del inglés), cada compensador fue discretizado mediante el método de retenedor de orden cero, con una frecuencia de muestreo de 10 kHz [24], [37].

3. Resultados de Simulación

En esta sección se presentan resultados de simulación del sistema de generación eléctrica propuesto. Los parámetros más importantes del GI, de la carga y de cada compensador PI se muestran en la Tabla 1. Dónde: P es la potencia nominal del motor; R_s y R_r son resistencias del estator y del rotor, respectivamente; L_s y L_r son inductancias del estator y del rotor, respectivamente; L_M es la inductancia de magnetización; L y C son los componentes del filtro LC y J es el momento de inercia del motor.

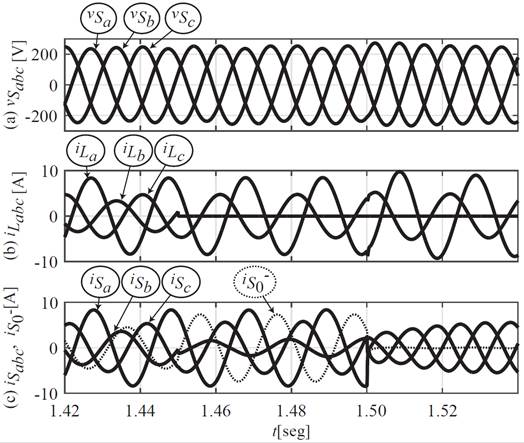
Al inicio de la simulación el GI se encuentra funcionando en vacío y la fuente de corriente se encuentra inyectando potencia reactiva a la barra de CA, para regular su tensión. En la Fig. 5 se presenta la evolución de las formas de onda de las tensiones del generador (v_Sabc), las corrientes de carga (i_Labc), las corrientes de fase (i_Sabc) y de neutro (i_S0).

En t = 1.42 seg, el generador se encuentra alimentando a las cargas desequilibradas 1 y 2 de la Tabla 1, conectadas en paralelo, con el algoritmo de compensación de desequilibrio de carga deshabilitado, por lo cual las corrientes de la MI (i_Sabc) de la Fig. 5 (c) son desequilibradas. Continuando en este modo de funcionamiento, en t = 1.45 seg se desconecta la carga de la fase b, en consecuencia, i_Lb se anula e i_S0 aumenta, como puede observarse en la Fig. 5 (b) y (c).

Tabla 1. Características de los componentes de simulación

Máquina de Inducción (MI)
Parámetro	Valor	Parámetro	Valor
P (kW)	3.30	Rr (Ω)	0.40
Rs (Ω)	1.80	Lr (mH)	5.75
Ls (mH)	5.75	LM (mH)	134.21
L (mH)	3	C (µF)	100
Nº de polos	4	J (kgm²)	0.04
Cargas
Carga 1		Carga 2
r1 = 400 (Ω),  L1 = 3 (mH)		rp1=30 (Ω)
		rp2=60 (Ω)
		rp3=90 (Ω)
Parámetros de los compensadores PI
PI	Kp	Ki	Ts(seg)
PIv	0.30	3	0.10
PIi	0.03	3	0.01
PIi0	0.40	3	0.01

En t = 1.5 seg se habilita el algoritmo de compensación de desequilibrio de carga, lo que hace que la fuente de corriente inyecte corriente de compensación a las tres fases y al conductor de neutro, en ese instante se observa, en la Fig. 5, que las tensiones y corrientes del GI se equilibran y la i_S0 se anula.

En la Tabla 2 se resumen los porcentajes de desequilibrio, cuando el sistema de generación eléctrica funciona sin el algoritmo de compensación (SC) y cuando si lo hace (C). Puede observarse en esta tabla que las tensiones de línea (U_L) tienen 0.74% de desequilibrio para el caso SC y 0.55% para el caso C. Es importante resaltar que el máximo de desequilibrio permitido por el standard IEEE 1159 es del 2%. El desequilibrio de corrientes de fases resultó 11.11% para el caso SC y 2.07% para el caso C, con un máximo permitido por la misma norma del 15%. Estos valores de desequilibrios (d) fueron calculados en función de la citada norma, mediante la siguiente ecuación:

(4)

Tabla 2.Porcentaje de desequilibrio de tensión de línea y corriente de fase del GI.

Variable	SC (%)	C (%)	Máx.
𝑈𝐿 (V)	0.74	0.55	2%
𝐼𝐹 (A)	11.11	2.07	15%

donde U_Lpromedio es el promedio de las tensiones instantáneas de línea. Se utilizó la misma expresión, modificada adecuadamente, para el caso de las corrientes.

Los resultados de desequilibrios obtenidos muestran la validez de la propuesta para compensar corriente de neutro, equilibrando corrientes y tensiones del GI.

Fig. 5. Formas de onda de tensiones y corrientes, cuando el GI alimenta una carga lineal desequilibrada de 2,3 kW con y sin la utilización del algoritmo de compensación: (a) v_Sabc, (b) i_Labc y (c) i_Sabc e i_S0.

4. Implementación Experimental de la Propuesta

En esta subsección se presenta el prototipo experimental implementado, cuyo circuito simplificado y fotografía se muestran en la Fig. 2 y la Fig. 6, respectivamente. Se utilizaron dos MI tipo jaula de ardilla convencionales, haciendo funcionar a uno como generador y al otro como motor primario. Las características de ambas maquinas se presentan en la Tabla 3. Además, en la Tabla 4 se muestran las características de los componentes más importantes del prototipo. Se utilizó un DSP de la familia de Texas Instruments^TM, el TMS320F28335, en el cual se implementaron los algoritmos de adquisición de las mediciones de las variables eléctricas, de control, de protecciones, de modulación de la fuente de corriente, entre otros.

Fig. 6. Prototipo experimental del sistema de generación eléctrica propuesto.

Tabla 3. Características de las máquinas de inducción.

MI - Generador (WEG/W22)
Parámetro/Componente	Valor	Parámetro/Componente	Valor
P (kW)	5.50	Rr (Ω)	0.40
Vs (VLinea,rms) ΔY	220/380	Is (A)	15.1/8.77
Rs (Ω)	1.16	Lr (mH)	5.74
Ls (mH)	5.74	LM (mH)	134.21
Nº de polos	4	J (kgm²)	0.04
Velocidad (RPM) 1500
MI - Motor primario (SIEMENS/IE1)
P (kW)	5.50	Rr (Ω)	0.40
Rs (Ω)	0.80	Lr (mH)	4
Ls (mH)	4	LM (mH)	125
Nº de polos	4	J (kgm²)	0.04
Velocidad (RPM) 1500

Para la medición de las variables eléctricas se utilizaron:

o tres sensores de tensión de efecto hall para medir las tensiones de fase a bornes del generador y un cuarto para medir la tensión de la barra de CC de la fuente de corriente.

o seis sensores de corriente de efecto hall, tres utilizados para medir las corrientes a la salida de la fuente de corriente y otros tres para medir las corrientes de carga.

o un sensor de posición para medir la velocidad del GI, acoplado al eje de ambas máquinas.

4.1. Resultados Experimentales

Para verificar el sistema de generación eléctrica propuesto, de manera similar a lo realizado en simulación, al inicio del ensayo experimental se llevó al sistema, en vacío, a valores nominales de funcionamiento; regulando la tensión en la barra de CA mediante la inyección de potencia reactiva desde la fuente de corriente. En estas condiciones, se conectó al GI una carga lineal y desequilibrada de 1 kW, dada por las tres resistencias monofásicas conectadas en estrella, indicadas como Carga 1 en la Tabla 4. Además, en estas condiciones, se puede observar que la fase b no tiene carga con el objetivo de provocar un sistema muy desequilibrado.

Tabla 4. Otros componentes del sistema propuesto.

Parámetro/componente	Características	Unidad/Rango
C	60	µF
L	5.5	mH
Sensores de corriente	LA 55p	0-50 A
Sensores de tensión	LV 25p	0-500 V
IGBT	SKM75GB124	1200 V y 75 A
Circuitos de activación	SKHI 22A
Sensor posición	1xp8001–1024p/v
Carga (CA)	ra = 115, rb = ∞, rc = 22.5	Ω
Tensiones	VSabc = 110, Vcc = 400	V

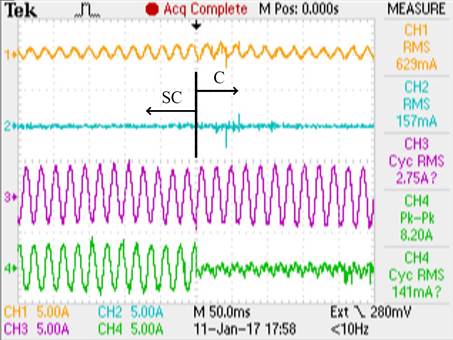
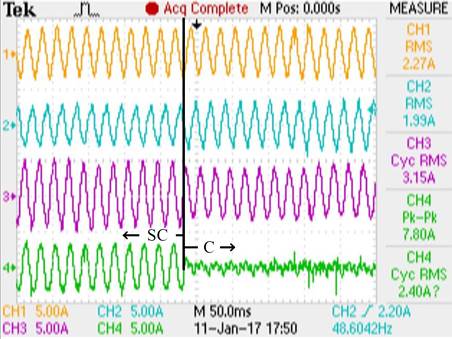
En la Fig. 7(a) se presentan las evoluciones de las corrientes de carga (i_La, i_Lb e i_Lc) y del neutro del GI (i_S0), antes y después de la compensación. En la Fig. 7 (b) se presentan las evoluciones de las tres corrientes de fase del generador (i_Sa, i_Sb y i_Sc) y para comparación, también, la del neutro del GI (i_S0).

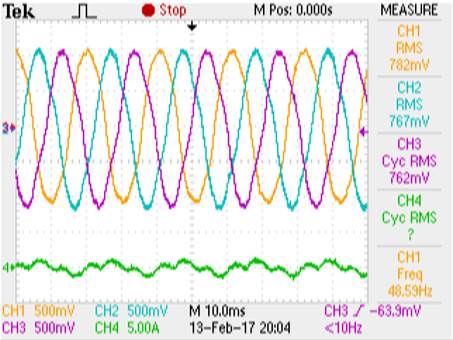
En las Figuras 7(c) y 7(d) se presentan, para el mismo ensayo, las evoluciones de las tensiones de fase del GI (v_Sabc) y de la corriente de neutro (i_S0) del sistema sin compensar y compensado, respectivamente.

Puede observarse en la Fig. 7 que luego de activar el algoritmo de compensación la corriente i_S0 disminuye su valor hasta hacerse prácticamente nula, además, que las corrientes y tensiones de fase del generador se equilibran. Esto se debe a que la fuente de corriente inyecta en el PCC corrientes de secuencia cero en oposición a la de la carga (−i_0L) y también corrientes de secuencia negativa en oposición a las producidas por el desequilibrio de carga.

5. Conclusiones

En este trabajo se propone la aplicación de la Teoría de Potencia Instantánea a un sistema de generación trifásica de cuatro hilos, capaz de alimentar cargas lineales monofásicas y/o trifásicas desequilibradas. Este sistema incluye la utilización de máquinas eléctricas rotativas, específicamente un motor de inducción (MI) del tipo jaula de ardilla, un sistema de excitación

compuesto por un banco de capacitores y un convertidor CC−CA de cuatro piernas que actúa como fuente de corriente, todos conectados en paralelo y formando lo que denominamos Generador de Inducción (GI).

Las principales ventajas que se tienen con esta propuesta son su bajo costo, la adecuada robustez y la mínima necesidad de mantenimiento, debido a la utilización de una maquina eléctrica rotativa como la MI de jaula de ardilla, mínimo valor de par pulsante, tensiones y corrientes del MI sinusoidales y equilibradas, mínimo valor de corriente de neutro, regulación con buena precisión y respuesta dinámica de la tensión de carga. Con estas características se logra que aumente el rendimiento y vida útil del GI.

Se validó la propuesta mediante resultados de simulación y experimentales verificándose muy buen desempeño tanto en funcionamiento en régimen transitorio como permanente del GI, principalmente en el funcionamiento con carga desequilibrada; que es el caso más desfavorable. Los resultados obtenidos, hacen que la propuesta en general sea una opción para la implementación de generadores trifásicos, para el suministro de energía eléctrica con buena calidad.

Agradecimientos

Agradecemos el financiamiento de este trabajo a la Facultad de Ingeniería de Universidad Nacional de Misiones (UNaM) en el marco del Proyecto de Investigación 16/I1205-PI (T. Inv. 16/I1090-TI) y al Concejo Nacional de Investigaciones Científicas (CONICET).

(a) Corrientes de carga: iLabc  (CH1,2,3) y de neutro: iS0(CH4).	(b) Corrientes de fase del GI: iSa,b,c (CH1,2,3) y de neutro: iS0 (CH4)
(c) Tensiones del GI vSabc (CH1,2,3) y corriente de neutro iS0 (CH4). Sistema sin compensador (SCC).	(d) Tensiones del GI vSabc (CH1,2,3) y corriente de neutro iS0 (CH4). Sistema con compensador (C).
Fig. 7. Ensayo de funcionamiento del algoritmo de compensación de desequilibrio de carga.

Referencias

[1]	M. Nehrir, C. Wang, K. Strunz, H. Aki, R. Ramakumar, J. Bing, Z. Miao, and Z. Salameh, “A review of hybrid renewable/alternative energy systems for electric power generation: Configurations, control, and applications,” IEEE Transactions on Sustainable Energy, vol. 2, no. 4, pp. 392–403, 2011.
[2]	S. Chu and A. Majumdar, “Opportunities and challenges for a sustainable energy future,” nature, vol. 488, no. 7411, pp. 294–303, 2012.
[3]	F. Blaabjerg, Y. Yang, K. Ma, and X. Wang, “Power electronics - the key technology for renewable energy system integration,” in 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Nov 2015, pp. 1618–1626.
[4]	M. Singh, S. P. Singh, B. Singh, A. S. Pandey, R. Dixit, and N. Mittal, “Stand alone power generation by 3 ϕ asynchronous generator: A comprehensive survey,” in 2012 2nd International Conference on Power, Control and Embedded Systems, Dec 2012, pp. 1–14.
[5]	J. Laghari, H. Mokhlis, A. Bakar, and H. Mohammad, “A comprehensive overview of new designs in the hydraulic, electrical equipments and controllers of mini hydro power plants making it cost effective technology,” Renewable and Sustainable Energy Reviews, vol. 20, pp. 279–293, 2013.
[6]	Z. Chen, J. Guerrero, and F. Blaabjerg, “A review of the state of the art of power electronics for wind turbines,” Power Electronics, IEEE Transactions on, vol. 24, no. 8, pp. 1859–1875, Aug 2009.
[7]	L. Gumilar, W. S. Nugroho, and M. Sholeh, “Power quality of synchronous generator under conditions of starting large induction motors simultaneously and sequentially,” in 2021 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), 2021, pp. 66–71.
[8]	P. Aree, “Starting performance of induction motor under isolated self-excited induction geneator,” in 2015 12th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), 2015, pp. 1–5.
[9]	M. H. Haque and A. Maswood, “Determination of excitation capacitance of a three-phase self-excited induction generator,” in Power and Energy Society General Meeting, 2012 IEEE, July 2012, pp. 1–6.
[10]	P. J. Chauhan and J. K. Chatterjee, “A novel speed adaptive stator current compensator for voltage and frequency control of standalone seig feeding three-phase four-wire system,” IEEE Transactions on Sustainable Energy, vol. 10, no. 1, pp. 248–256, Jan 2019.
[11]	M. Kiani and W.-J. Lee, “Effects of voltage unbalance and system harmonics on the performance of doubly fed induction wind generators,” IEEE Transactions on Industry Applications, vol. 46, no. 2, pp. 562–568, 2010.
[12]	A. K. Sharma, “Study of wind turbine based seig under balanced/unbalanced loads and excitation,” International Journal of Electrical and Computer Engineering, vol. 2, no. 3, p. 353, 2012.
[13]	C. Wessels, N. Hoffmann, M. Molinas, and F. W. Fuchs, “Statcom control at wind farms with fixed-speed induction generators under asymmetrical grid faults,” IEEE Transactions on Industrial Electronics, vol. 60, no. 7, pp. 2864–2873, 2013.
[14]	F. B. Silva, W. E. Vanco, F. A. da Silva Goncalves, C. A. B. Junior, D. P. de Carvalho, and L. M. Neto, “Experimental analysis of harmonic distortion in isolated induction generators,” IEEE Latin America Transactions, vol. 14, no. 3, pp. 1245–1251, 2016.
[15]	V. S. Santos, P. R. V. Felipe, J. R. G. Sarduy, E. C. Quispe, and M. Balbis, “Shaft power estimation in induction motor operating under unbalanced and harmonics voltages,” IEEE Latin America Transactions, vol. 14, no. 5, pp. 2309–2315, 2016.
[16]	G. Carrasco, C. A. Silva, R. Pe˜na, and R. C´ardenas, “Control of a four-leg converter for the operation of a dfig feeding stand-alone unbalanced loads,”IEEE Transactions on Industrial Electronics, vol. 62, no. 7, pp. 4630–4640, July 2015.
[17]	M. Szypulski and G. Iwanski, “Sensorless state control of stand-alone doubly fed induction generator supplying nonlinear and unbalanced loads,” IEEE Transactions on Energy Conversion, vol. 31, no. 4, pp. 1530–1538, Dec 2016.
[18]	A. A. Abdel-Aziz, R. A. Hamdy, and A. S. Abdel-Khalik, “Design and performance evaluation of a three-phase self-excited induction generator feeding single-phase loads,” Electric power components and systems, vol. 47, no. 6-7, pp. 486–500, 2019.
[19]	E. Muljadi, D. Yildirim, T. Batan, and C. P. Butterfield, “Understanding the unbalanced-voltage problem in wind turbine generation,” in Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting (Cat. No.99CH36370), vol. 2, 1999, pp. 1359–1365 vol.2.
[20]	V. Leon-Martinez, J. Montanana-Romeu, and J. M. Palazon-Garcia, “Unbalance compensator for three-phase industrial installations.” IEEE Latin America Transactions, vol. 9, no. 5, pp. 808–814, 2011.
[21]	A. K. Panigrahi, R. Kulkarni, and D. Sadhu, “Design and simulation of innovative hybrid filter for harmonic compensation,” in 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), 2016, pp. 1–6.
[22]	B. Singh, S. Murthy, and R. S. R. Chilipi, “Statcom-based controller for a three-phase seig feeding single-phase loads,” IEEE transactions on energyconversion, vol. 29, no. 2, pp. 320–331, 2014.
[23]	L. G. Scherer, R. V. Tambara, and R. F. de Camargo, “Voltage and frequency regulation of standalone self-excited induction generator for micro-hydropower generation using discrete-time adaptive control,” IET Renewable Power Generation, 2016.
[24]	L. G. Scherer, C. B. Tischer, and R. F. de Camargo, “Power rating reduction of distribution static synchronous compensator for voltage and frequencyregulation of stand-alone self-excited induction generator,” Electric Power Systems Research, vol. 149, no. Supplement C, pp. 198 – 209, 2017.[Online]. Available: http://www.sciencedirect.com/science/article/pii/S0378779617301608
[25]	Z. Chen, J. Lu, C. Mao, Y. Zhou, and D. Wang, “Design and implementation of voltage source converter excitation system to improve power systemstability,” in 2015 IEEE Industry Applications Society Annual Meeting, 2015, pp. 1–10.
[26]	H. Akagi, “New trends in active filters for power conditioning,” Industry Applications, IEEE Transactions on, vol. 32, no. 6, pp. 1312–1322, Nov 1996. 11
[27]	E. W. y M. Aredes H. Akagi, Instantaneous Power Theory and Applications to Power Conditioning. IEEE Press Series on Power Engineering, 2007.
[28]	P. Kumar, A. K. Singh, and N. K. Kummari, “p-q theory based modified control algorithm for load compensating using dstatcom,” in 2014 16^th International Conference on Harmonics and Quality of Power (ICHQP), 2014, pp. 591–595.
[29]	R. Leidhold, G. Garc´ıa, and M. I. Valla, “Induction generator controller based on the instantaneous reactive power theory,” Power Engineering Review, IEEE, vol. 22, no. 7, pp. 51–51, July 2002.
[30]	P. Silva, R. Pinheiro, M. Aguiar, L. Junior, A. Salazar, and C. Cunha, “Implementation of a shunt active filter using the theory of generalized instantaneous power,” in Power Electronics Conference (COBEP), 2011 Brazilian, Sept 2011, pp. 782–787.
[31]	B. A. J., de la B. Pablo M, and G. G. O, “Sistema de excitaci´on y compensaci´on de arm´onicos para generadores de inducci´on jaula de ardilla,” in Biennial Congress of Argentina (ARGENCON), 2014 IEEE. IEEE, 2014, pp. 73–77.
[32]	A. J. Benitez, F. Botter´on, and G. Garcıa, “Autonomous induction generator feeding non-linear and unbalanced loads,” in 2018 IEEE Biennial Congress of Argentina (ARGENCON), 2018, pp. 1–6.
[33]	M. Aredes, H. Akagi, E. H. Watanabe, E. V. Salgado, and L. F. EncarnaC¸A˜ o, “Comparisons between the p–q and p–q–r theories in three-phase four-wire systems,” IEEE Transactions on Power Electronics, vol. 24, no. 4, pp. 924–933, 2009.
[34]	F. Rodriguez, E. Bueno, M. Aredes, L. Rolim, F. A. Neves, and M. C. Cavalcanti, “Discrete-time implementation of second order generalized integrators for grid converters,” in Industrial Electronics, 2008. IECON 2008. 34th Annual Conference of IEEE. IEEE, 2008, pp. 176–181.
[35]	E. M. Asensio, G. A. Magall´an, and C. H. De Angelo, “Control de un sistema h´ıbrido de almacenamiento de energ´ıa para veh´ıculos el´ectricos,” in 2014 IEEE Biennial Congress of Argentina (ARGENCON), June 2014, pp. 570–575.
[36]	F. Botterón, R. De Camargo, H. Hey, J. Pinheiro, H. Grundling, and H. Pinheiro, “New limiting algorithms for space vector modulated three-phase four-leg voltage source inverters,” IEE Proceedings-Electric Power Applications, vol. 150, no. 6, pp. 733–742, 2003.