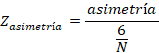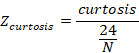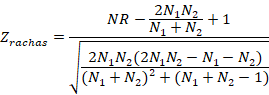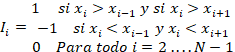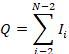|
|
Vol. 5 N°1, enero-junio 2024, pág. 9-24
ISSN 2618-5520 online - ISSN 2683-7021 impresa
DOI: https://doi.org/10.36995/j.masingenio.2024.05.01.001
Análisis de homogeneidad, tendencias y saltos de las precipitaciones en la Provincia de Misiones
Ariana Giselle Seufert a,b (https://orcid.org/0009-0009-5696-1293)
a Universidad Nacional de Misiones. Facultad de Ingeniería. Misiones, Argentina.
b Consejo Nacional de Investigaciones Científicas y Tecnológicas (CONICET).
c Universidad Nacional de Cuyo. Departamento de Geografía, Facultad de Filosofía y Letras. Mendoza, Argentina.
d Centro Científico Tecnológico CONICET – MENDOZA.
e-mails: fatima.schoninger@fio.unam.edu.ar, aijvich@mendoza-conicet.gob.ar, dario.rodriguez@fio.unam.edu.ar, jose.fernandez@fio.unam.edu.ar, ariana.seufert@fio.unam.edu.ar
Resumen
A partir de la necesidad de la gestión integral de recursos hídricos, los hidrólogos requieren conocer los componentes del ciclo hidrológico y su comportamiento ante la presencia del cambio climático. Actualmente muchos investigadores dirigen sus estudios a la identificación de tendencias en series de variables hidrometeorológicas, utilizando pruebas paramétricas y no paramétricas. En este artículo se presenta un análisis de precipitaciones del periodo 1991-2018 para 14 estaciones de la provincia de Misiones. Tiene como objetivo detectar tendencias o cambios graduales y cambios abruptos o saltos en los valores medios de una serie de precipitaciones de 28 años, en una región que evidencia carencia de datos confiables con relación a la variabilidad de precipitaciones en la provincia. Para ello, se estudió previamente las condiciones de normalidad, aleatoriedad e independencia, para luego realizar el análisis de tendencias o saltos. Además, se evaluó la consistencia y homogeneidad de datos. Se realizó un análisis exploratorio de datos considerando los supuestos de normalidad, aleatoriedad e independencia, donde el 13% de los datos no cumple con uno o más de los tres supuestos. Además, se llevaron a cabo pruebas paramétricas y no paramétricas para detectar tendencias y saltos en la serie, que arrojaron como resultados que el 5% de los datos presenta una tendencia, de los cuales el 69% es positiva y el 31% con tendencias negativas. Con respecto a los saltos detectados el 58% resultaron ser positivo.
Palabras Clave: Precipitaciones, Serie de datos, Tendencia, Salto, Homogeneidad de datos.
Abstract
Based on the need for comprehensive management of water resources, hydrologists need to know the components of the hydrological cycle and their behavior in the presence of climate change. Currently, many researchers direct their studies to identify trends in series of hydrometeorological variables, using parametric and non-parametric tests. This article presents an analysis of rainfall during the period 1991-2018 for 14 stations in the province of Misiones. The objective is to detect trends or gradual changes and abrupt changes or jumps in average values of a 28-year series of rainfall, considering there is a lack of reliable data regarding the variability of rainfall in the province. For this, the conditions of normality, randomness and independence were previously studied, to then carry out analysis of trends or jumps. In addition, the consistency and homogeneity of data was evaluated. An exploratory data analysis was carried out taking into account the assumptions of normality, randomness and independence, where 13% of the data does not meet one or more of the three assumptions. Furthermore, parametric and non-parametric tests were conducted to detect trends and jumps in the series. The analysis revealed that 5% of the data presents a trend, of which 69% are positive and 31% negative. Regarding the jumps detected, 58% turned out to be positive.
Keywords: Rainfall, Data series, Trend, Jump, Data homogeneity.
1. Introducción
Ubicada sobre el Acuífero Guaraní, uno de los reservorios de agua dulce más grande del mundo, la Selva Misionera, también conocida como Selva Paranaense, Selva Atlántica, ocupa la tercera parte del territorio de la provincia de Misiones. Las precipitaciones promedio de 1800 mm anuales, conllevan un alto porcentaje de humedad y un clima subtropical sin estación seca [1] y 2]. El sistema hídrico de Misiones cuenta con tres ríos principales que son el Paraná, el Iguazú y el Uruguay, además de estos importantes cursos de agua, se hallan aproximadamente 800 arroyos dentro del territorio provincial. La mayoría de estos cauces internos nacen en el sector de las Sierras Centrales y en la altiplanicie del departamento de San Pedro, el gran centro dispersor de aguas, y desde allí bajan formando saltos y cascadas con ecosistemas de gran diversidad biológica [3].
Sin embargo, la expansión de la frontera agrícola se ha identificado como la mayor amenaza para la reducción de los bosques en la región misionera y como consecuencia una posibilidad de variabilidad climática. El incremento de los cultivos como soja, caña de azúcar, maíz, trigo, tabaco, yerba mate, té y plantaciones de pino y eucalipto, además de la cría de ganado, la caza con fines comerciales, culturales o de subsistencia, las altas tasas de crecimiento poblacional y el escaso conocimiento de los problemas ambientales de la ecorregión por parte de sus pobladores, entre otras causales, son los responsables de la degradación de la selva sumado a la explotación tradicional del monte nativo [3].
Históricamente en la región serrana de Misiones, la selva Paranaense autóctona ha contribuido a minimizar las afectaciones negativas desencadenadas por las intensas precipitaciones, reduciendo los volúmenes de escurrimiento directo y las velocidades de flujo, a la vez que el sistema radicular aporta al sustento del suelo, mitigando los procesos erosivos y optimizando por procesos de infiltración y almacenamiento de humedad en el suelo. Sin embargo, en los últimos años se acentuó el cambio de las condiciones hidroambientales de la región, presentándose mayor variabilidad en el régimen de precipitaciones, particularmente de los extremos (máximos o mínimos) [4]. Diversos autores, entre ellos Dickie y Coronel creen indispensable incorporar a la gestión de los recursos hídricos consideraciones sobre el Cambio Climático (CC). Particularmente, [4] en su informe “Cambio climático, breve historia y tendencias en la Región Húmeda” para la región comprendida por las provincias de Corrientes y Misiones, se observa un aumento paulatino de las temperaturas mínimas, medias y máximas, se registró un aumento en las precipitaciones medias anuales de 94,1 mm (representando un aumento del orden 5% en 60 años para la región). Además, los autores afirman que dicho aumento se produjo en todas las estaciones del año, excepto en el invierno en el que prácticamente hubo una disminución de la precipitación. Esta última conclusión hace presuponer que, además de un aumento de las precipitaciones existe una tendencia a la concentración de las lluvias en los meses no invernales.
En el presente artículo se estudia los supuestos de la normalidad, aleatoriedad e independencia de las precipitaciones. Asimismo, se detectaron los cambios graduales o tendencias y saltos o cambios abruptos en el régimen de precipitaciones de la provincia de Misiones mediante la aplicación de test paramétricos y no paramétricos. Para ello se utilizaron los registros de 14 estaciones del Sistema Nacional de Información Hídrica de la Red hidrológica Nacional comprendida desde el año 1991 hasta el 2018, es decir una serie de 28 años.
2. Metodología
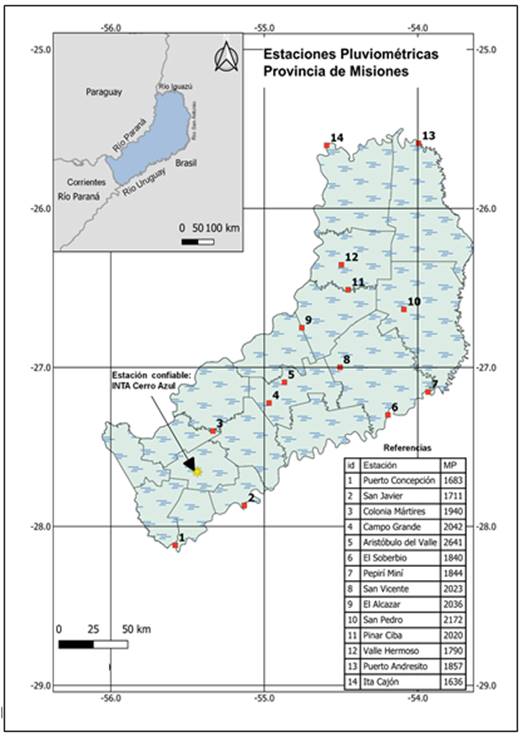
Se realizó un análisis de los datos de precipitaciones de 14 estaciones proporcionadas por el Sistema Nacional de Información Hídrica de la Red hidrológica Nacional para el periodo comprendido entre los años 1991 al 2018, se consideró este periodo por contar con la mayor cantidad de información. Los datos mensuales faltantes se completaron con el método directo, siguiendo a Orsolini et al. [5]. Se aplicó el método de dobles acumulaciones para analizar la consistencia de datos de las 14 estaciones estudiadas por comparación con los datos confiables de la estación del INTA de Cerro Azul. Las estaciones analizadas se presentan en la Tabla 1 y se visualizan geográficamente en la Fig. 1.
Tabla 1: Estaciones analizadas.
|
Estación |
Nombre |
Latitud Sur |
Longitud Oeste |
|
E1 |
Puerto Concepción |
28º 07' 07,6" |
55º 34' 51,6" |
|
E2 |
San Javier |
27° 52' 8,4'' |
55° 07' 48'' |
|
E3 |
Colonia Mártires |
27° 24' 3,6'' |
55° 20' 06'' |
|
E4 |
Campo Grande |
27° 13' 26,4'' |
54° 58' 8,4'' |
|
E5 |
Aristóbulo del Valle |
27° 05' 38,4'' |
54° 52' 8,4'' |
|
E6 |
El Soberbio |
27° 17' 56,4'' |
54° 11' 38,4'' |
|
E7 |
Pepirí Miní |
27° 9' 14,4'' |
53° 55' 58,8'' |
|
E8 |
San Vicente |
27° |
54° 30' 25,2'' |
|
E9 |
El Alcázar |
26° 45' 3,6'' |
54° 45' 21,6'' |
|
E10 |
San Pedro |
26° 38' 6'' |
54° 5' 24'' |
|
E11 |
Pinar Ciba |
26° 30' 43.2'' |
54° 27' 14,4'' |
|
E12 |
Valle Hermoso |
26° 21' 18'' |
54° 29' 52,8'' |
|
E13 |
Puerto Andresito |
25° 35' 27,6'' |
53° 59' 42'' |
|
E14 |
Itá Cajón |
25° 36' 14,4'' |
54° 35' 34,8'' |
|
E15 |
INTA Cerro Azul |
27° 39' 24,7'' |
55° 26' 13.4'' |
|
|
Fig. 1: Estaciones analizadas.
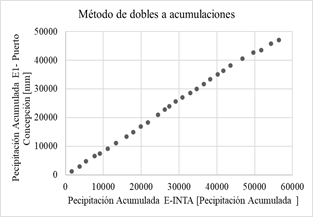
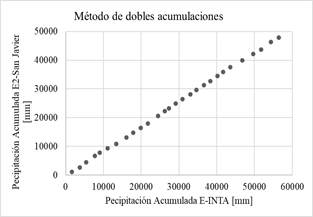
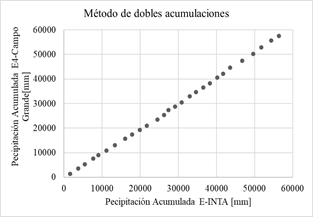
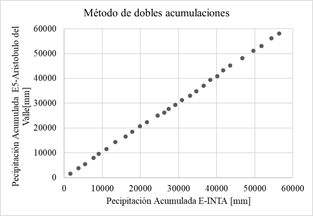
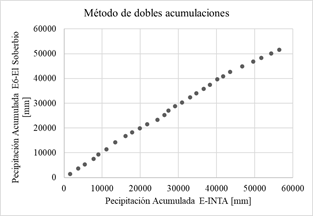
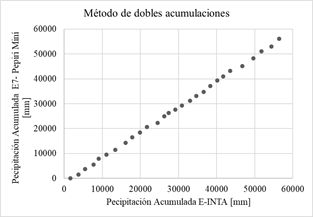
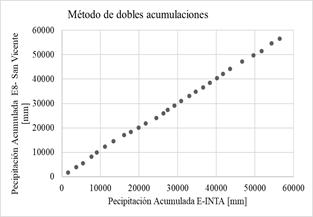
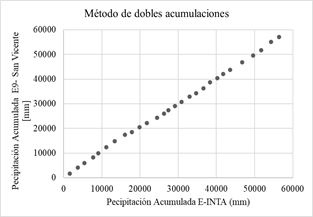
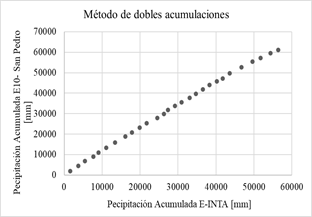
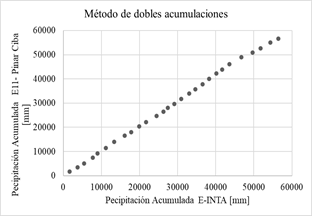
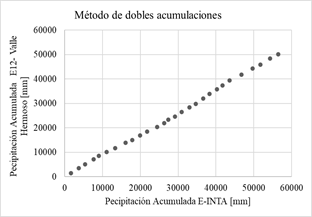
Si los valores acumulados de cada estación en cuestión son proporcionales a los valores acumulados de la estación de confianza, se obtiene una recta cuya pendiente representa el coeficiente de proporcionalidad. Se considera a los datos inconsistentes si, a partir de un determinado momento, se observa un cambio de pendiente formado por más de cinco puntos, en ese caso no se consideran representativos [5].
La población a estudiar es el conjunto de datos de 14 estaciones meteorológicas de la provincia de Misiones, donde la muestra representativa de esta población son los datos mensuales de precipitación de cada una de las mismas.
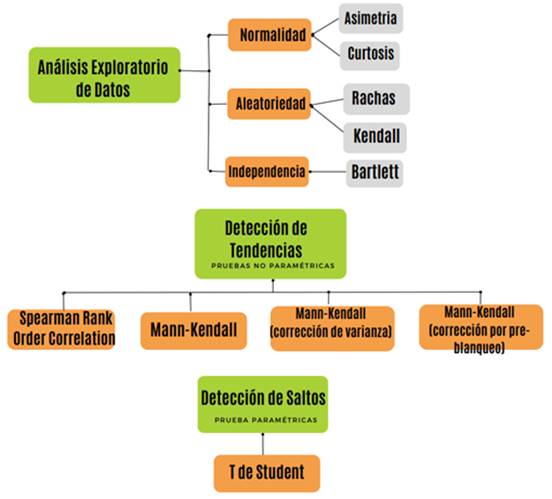
A partir de los módulos anuales y por medio de diferentes test estadísticos simples se detectó la existencia de aleatoriedad o una secuencia en los datos, cambios graduales o abruptos, Fig. 2. Además, para aplicar los test paramétricos según Lauro et al. [6], los datos deben contar con la hipótesis de normalidad, si la misma es rechazada, el test pierde robustez, es decir es dudoso [7].
|
|
Fig. 2: Test empleados para el análisis de la serie de precipitaciones.
Para el supuesto
de Normalidad se usaron los siguientes test: ![]()
2.1 Test de Asimetría:
|
|
(1)
|
2.2 Test de Curtosis:
|
|
(2)
|
Siendo N el tamaño de la muestra. Si es cierta la hipótesis de normalidad ambos se distribuyen asintóticamente según una N(0,1) [7].
Para el supuesto de Aleatoriedad se usaron los siguientes test [6]-[8]:
2.3 Test de Rachas
Permite verificar la hipótesis nula de que la muestra es aleatoria, lo cual indica si las sucesivas observaciones son independientes. Este contraste se basa en el número de rachas (secuencia de valores sucesivos iguales) que presenta una muestra. Se asigna un indicador, según esté por encima o debajo de la mediana muestral, se establece el número de rachas y de datos que posee cada indicador:
|
|
(3) |
|
donde NR es el número de rachas y N1 y N2 el número de datos de los indicadores.
2.4 Test de Kendall
Permite comprobar la presencia de aleatoriedad en una muestra de datos, teniendo en cuenta el rango de una serie de puntos de inflexión, picos y valles que deberían distribuirse al azar.
|
|
|
(4) |
Se define una nueva serie (la antes mencionada) y se calcula el número de puntos de inflexión Q:
|
|
(5)
|
El estadístico de contraste C, tiene distribución aproximadamente normal N (0,1). Donde Q número de puntos de inflexión:
|
|
(6) |
2.5 Test de Bartlett:
Para el supuesto de independencia, se asume en este test, que las observaciones de la muestra siguen una distribución normal. La independencia de las observaciones en la serie se comprueba mediante el coeficiente de autocorrelación. La hipótesis nula es que la autocorrelación sea cero, lo que significa que los datos posteriores en la muestra son independientes. El coeficiente se calcula con la ecuación 7:
|
|
(7)
|
donde ![]() es el estadístico de contraste y los
grados de libertad
es el estadístico de contraste y los
grados de libertad ![]()
Se entiende como tendencia al cambio gradual a largo plazo en la media de una variable. La presencia de tendencia equivale a decir que la serie es no estacionaria. Para detectar tendencias o cambios graduales se usaron test no paramétricos de Spearman Rank Order Correlation Test (SROC), Mann-Kendall, y sus correcciones por varianza y pre-blanqueo.
2.6 Spearman Rank Order Correlation Test (SROC)
Es un test basado en un orden de rangos para medir la relación monótona entre dos variables que suelen censurarse y no se distribuyen normalmente. La correlación de orden de rango de Spearman se encuentra entre -1 y 1. La detección de la potencia de la prueba de correlación de rango de Spearman es importante en el análisis de los datos de serie temporal hidrológica [7].
2.7 Test de Mann-Kendall
Es ampliamente aplicado en estudio de identificación de tendencias en series hidrometereológicas y otras series ambientales. El test de Mann-Kendall es un test no paramétrico que permite identificar si existe una tendencia en la serie temporal que se desea estudiar, determina la tendencia (positiva, negativa o cero) de una muestra de N datos donde se conserva el orden cronológico en el que fueron tomados. La hipótesis nula establece que no hay una tendencia en el conjunto de datos [6], [8].
2.8 Test de Mann y Kendall con corrección de la varianza
Está basada en la corrección de la varianza en función del número efectivo de observaciones. Su importancia radica en que detecta tendencias que no existen realmente, lo que significaría rechazar la hipótesis nula cuando esta es cierta [6][8].
2.9 Test de Mann y Kendall con corrección por pre-blanqueo
Este procedimiento de pre-blanqueo es para eliminar el efecto de la correlación serial. Se basa en determinar una nueva serie de datos donde cada valor, es dividido por el promedio; luego, la tendencia y autocorrelación de primer orden es removida. Se recarga la tendencia y se aplica el test de Mann y Kendall original, donde se determina si la tendencia no paramétrica es estadísticamente distinta de cero. [6][8]
2.10 Test t de Student
Para detectar cambios abruptos en la serie de precipitaciones se recurrió al Test t de Student.
Este test detecta puntos de quiebre estadísticamente significativos de manera más frecuente que los otros test, para ello, debe eliminarse previamente la tendencia y la serie debe tener una distribución normal. Se basa en la verificación de la igualdad estadística de dos medias muestrales, lo que significa que ambas muestras pertenecen a la misma población y, por lo tanto, no ha habido cambios abruptos en el régimen de precipitaciones [6], [8]-[10].
3. Resultados
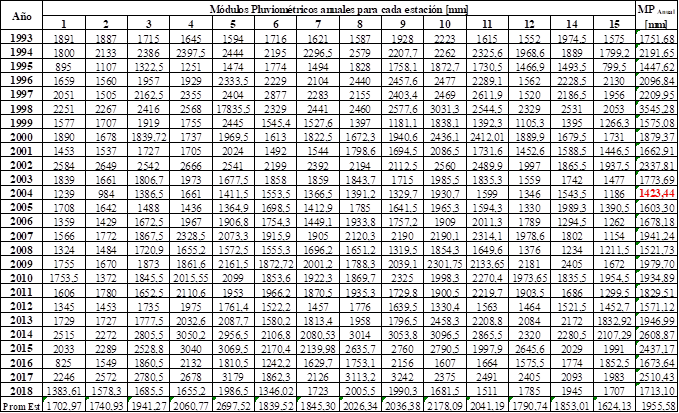
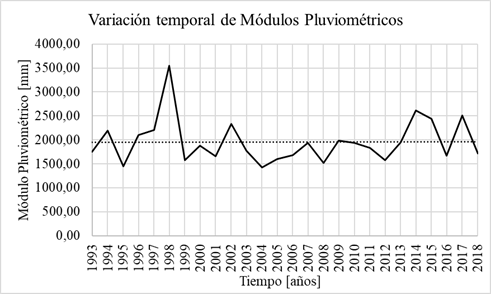
Se obtienen los módulos anuales de las precipitaciones para cada estación analizada, donde el menor valor de precipitación anual se produjo en el año 2004, coincidiendo con un período de escasas lluvias [1]. La media anual de precipitaciones (1955 mm) que se muestra en la Tabla 2, puede ser considerada como un valor climático para la zona analizada ya que es superior a los citados en las descripciones climáticas para esta región. La variación temporal de módulos pluviométricos anuales se muestra en la Fig. 3.
Tabla 2: Módulos pluviométricos anuales.
|
|
|
|
Fig. 3: Variación temporal de módulos pluviométricos anuales.
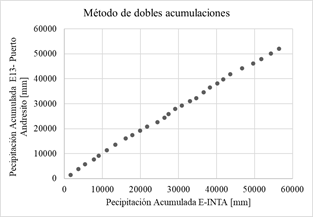
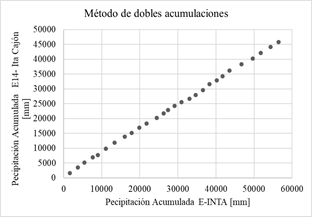
En las gráficas de la Fig. 4 se aplica el método de dobles acumulaciones, las precipitaciones acumuladas de cada una de las 14 estaciones proporcionadas por el Sistema Nacional de Información Hídrica de la Red hidrológica Nacional (eje vertical) son comparadas con los datos de precipitación acumulada de la estación confiable (eje horizontal) se considera que no hay inconsistencias representativas o errores sistemáticos.
|
|
|
|
|
|
|
|
|
|
Fig. 4: Método de dobles acumulaciones.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 4: Método de dobles acumulaciones (Continuación).
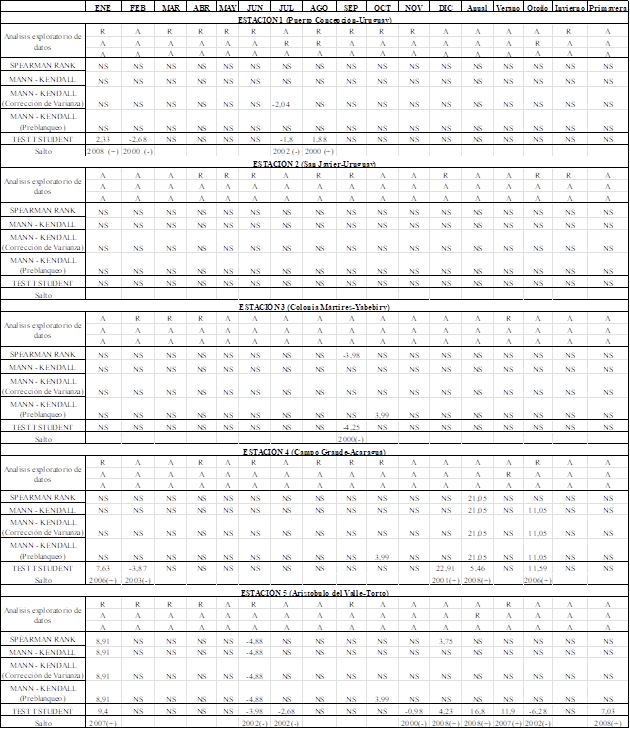
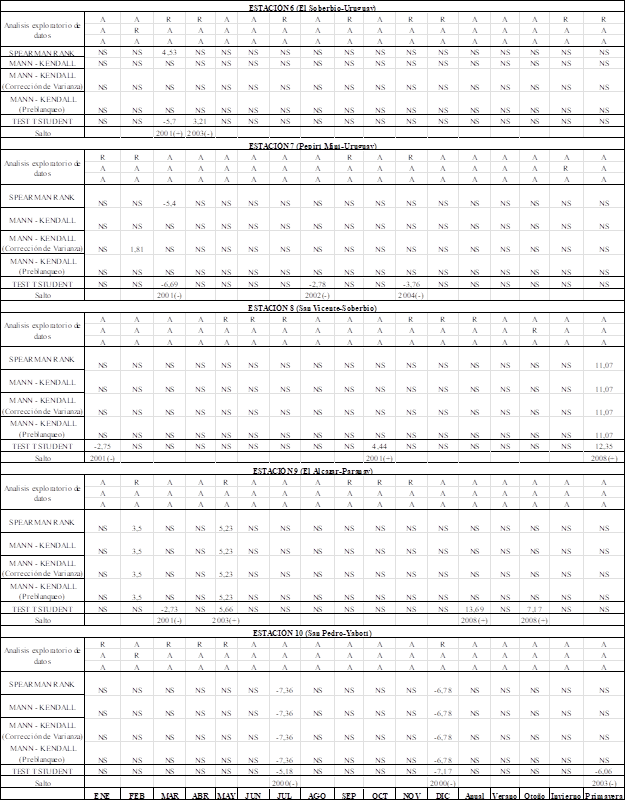
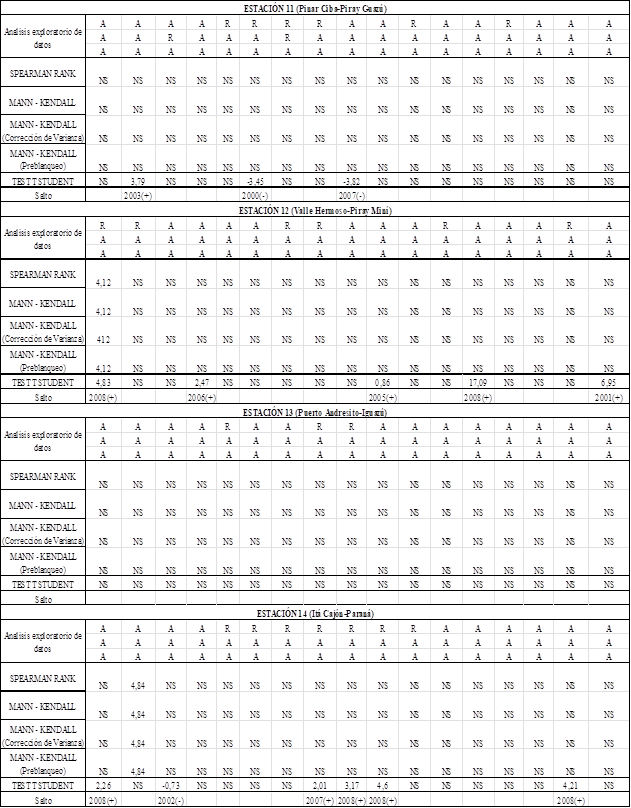
A continuación, se detallan los resultados del análisis estadístico realizados, en la Tabla 3, siguiendo la metodología descripta precedentemente, mediante un código en Fortran para los datos mensual, anual y estacional. En el cual, de enero a marzo, es verano; desde abril a junio, otoño; desde julio a septiembre, invierno; desde octubre a diciembre, primavera. Donde A=acepta, R=Rechaza (para los supuestos de Normalidad, Aleatoriedad e Independencia, en ese orden) y NS= No Significativo, el signo (-) y (+) indica si el salto es negativo o positivo.
Tabla 3: Resumen del análisis estadístico.
|
|
Tabla 3: Resumen del análisis estadístico (Continuación).
|
|
Tabla 3: Resumen del análisis estadístico (Continuación).
|
|
Los resultados del test de asimetría nos dan el criterio para rechazar o no la hipótesis nula de los datos provienen de una población distribuida normalmente. La hipótesis nula es que “No hay tendencia”. Por ende, cuando se acepta la hipótesis nula significa que la pendiente o tendencia es estadísticamente igual a cero, es decir que no hay tendencias significativas. Para determinar si los datos no siguen una distribución normal se toma α = 0.05, lo cual indica un riesgo de 5% de concluir que los datos no siguen una distribución normal.
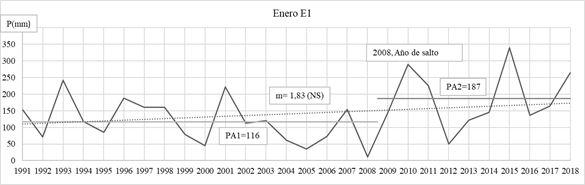
Los resultados obtenidos de los datos se interpretan mejor con ayuda de una representación gráfica. Por ello, a continuación, se detalla el análisis exploratorio de datos para la Estación 1: Puerto Concepción, donde para enero se rechaza (R) la prueba de normalidad, pero se Acepta (A) las de aleatoriedad e independencia.
|
|
Fig. 5: Salto E1.
|
|
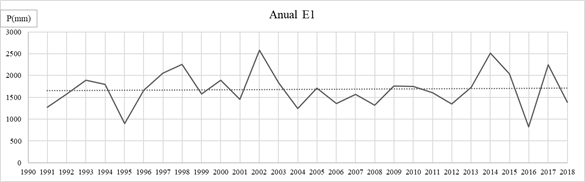
Fig. 6: Precipitaciones anuales E1.
|
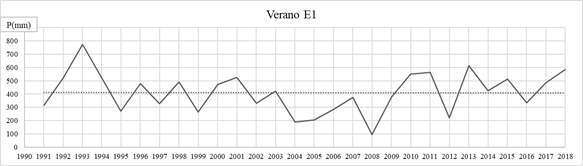
|
Fig. 7: Precipitaciones de Verano E1.
|
|
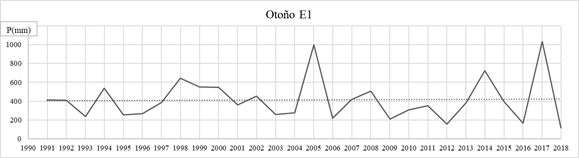
Fig. 8: Precipitaciones de Otoño E1.
|
|
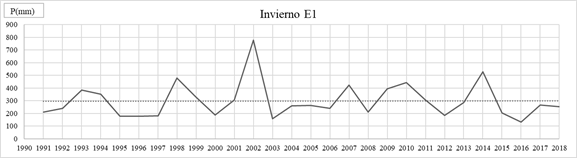
Fig. 9: Precipitaciones de Invierno E1.
|
|
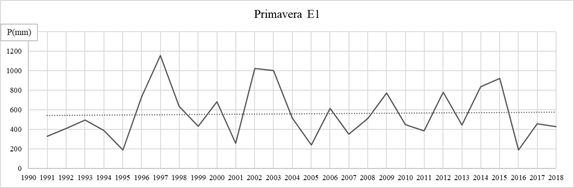
Fig. 10: Precipitaciones de Primavera E1.
Se observa con detalle para la E1: Puerto Concepción, en enero, febrero, julio y agosto hay cambios graduales. En julio y agosto no se cumple con el supuesto de aleatoriedad y en agosto además con el de normalidad, entonces hay una duda razonable y los datos son sospechosos, ya que el test de T de Student requiere de datos con distribución normal. En enero se observa una tendencia positiva, si bien es no significativa y presenta un salto positivo en el año 2008, donde la media mensual de precipitaciones pasa de 116 mm a 187 mm. Para los demás meses no se observan cambios graduales y/o abruptos, ni en el análisis estacional como tampoco en el anual. En las gráficas para las precipitaciones de verano, otoño, invierno, primavera y la de precipitaciones anual se puede observar que no hay tendencia significativa.
4. Conclusiones
Al observar los módulos anuales de la serie analizada, se detecta un leve cambio gradual. Al someterla a diferentes test estadísticos, se concluye que el cambio no es significativo.
El 87% de los datos cumple con los supuestos de Normalidad, Aleatoriedad e Independencia. El supuesto de Normalidad cumple el 65%, Aleatoriedad el 95% e Independencia el 100% de los datos.
El 95 % de los datos no presentó tendencias significativas, el 3,4% presenta tendencias positivas y el 1,5% de los datos presenta tendencias negativas.
Con respecto a los saltos detectados en el análisis, el 58% son positivos, siendo el 42% de los saltos negativos. Se puede ver que, coincidiendo con un período de escasas lluvias que abarcó los meses de noviembre de 2004 hasta marzo de 2005, se detecta un salto negativo en el 2004 y uno positivo en el 2005 que corresponde al término de los escases de lluvias.
Debido a que la mayoría de los datos cumplen con los supuestos de Normalidad, Aleatoriedad e Independencia, se puede aceptar, desde el punto de vista estadístico, que los cambios graduales presentados no son significativos.
La detección de puntos de cambio está asociada a la variabilidad climática natural. Se ha utilizado una prueba estadística que detecta un único punto de cambio. Se considera a futuro la utilización de alguna prueba de detección de múltiples puntos, para un análisis de mayor confiabilidad.
Referencias
|
[1] |
F. Silva, B. Eibl, E. Bobdilla, “Características de la Precipitación Durante 1981-2012 en Eldorado Misiones”, Revista Forestal Yvyrareta, vol 21, pp 36-42. 2014. |
|
[2] |
G. Prytz Nilson, A. G. Seufert, S. Ulrich, F. Schoninger, “Gestión de cuencas hidrográficas: Aplicaciones de SIG para mediciones pluviométricas”, en 9° Jornadas de Investigación, Desarrollo Tecnológico, Extensión, Vinculación y Muestra 2019. Facultad de ingeniería-UNaM, Oberá, Misiones. |
|
[3] |
Instituto Provincial de Estadística y Censos- Gobierno de la Provincia de Misiones, “Gran Atlas de Misiones”. 2015. |
|
[4] |
M. Dickie, A. Coronel, “Cambio climático, breve historia y tendencias en la Región Húmeda”, INTA EEA Oliveros, 2016. |
|
[5] |
H. Orsolini, E. Zimmermann, P. Basile, Hidrología, Procesos y Métodos. Editorial UNR. 2017. |
|
[6] |
C. Lauro, A. I. J. Vich, S. Moreiras, “Variabilidad del Régimen Fluvial en Cuencas de la Región de Cuyo”, GEOACTA, vol. 40, no. 2, pp. 28-51. 2016. |
|
[7] |
S. Figueras, P. Gargallo (2023, 05, 12). Análisis Exploratorio de Datos. [Online]. Available: http:/www.5campus.com/leccion/aed |
|
[8] |
A. I. J. Vich, F. Bizzotto, E. Vaccarino, M. Correas, F. Manduca, “Tendencias y cambios abruptos en el escurrimiento de algunos ríos con nacientes en la cordillera y serranías del oeste argentino”, en Criterios para la determinación de crecidas de diseño en sistemas climáticos cambiantes, Santa Fe: Universidad Nacional del Litoral, 2010, pp- 149-166. |
|
[9] |
A. Pardo, R. San Martín, Análisis de datos en ciencias sociales y de la salud. Universidad Autónoma de Madrid. 2010. |
|
[10] |
A. Poblete, J. Minetti, S. Escudero, “Cambios abruptos en los derrames anuales del río San Juan – Argentina asociados a fenómenos climáticos de la macroescala”, en XXIV Congreso Nacional del Agua 2013. San Juan, Argentina. |