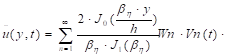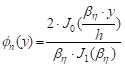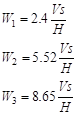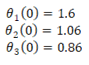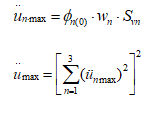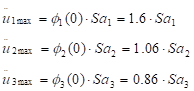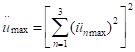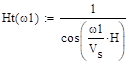Vol. 4 N° 2, julio-diciembre 2023, pag. 77-91
ISSN 2618-5520 on line
DOI - https://doi.org/10.36995/j.masingenio.2023.11.21.006
ANÁLISIS COMPARATIVO DEL
COMPORTAMIENTO DINÁMICO DE UNA PRESA DE MATERIALES SUELTOS
Bogado Gustavo Orlandoa , https://orcid.org/0000-0003-1807-9733, (Gustavo.bogado@fio.unam.edu.ar)
Panique Daniel Lazcanob,
https://orcid.org/0000-0002-7327-6839
Reinert Hugo Orlandoc, https://orcid.org/0000-0001-8926-6742, (hugo.reinert@fio.unam.edu.ar)
a CONICET, Universidad Nacional de Misiones, Facultad
de Ingenieria, Departamento de Ingeniería Civil
b Consultor Independiente, Madrid España
c Universidad Nacional de Misiones, Facultad de Ingenieria,
Departamento de Ingeniería Civil
La Comisión Internacional
de Grandes Presas (ICOLD) recomienda un enfoque del análisis dinámico en el
cual indica que las presas deben diseñarse por el método convencional en primer
lugar, seguido de un análisis dinámico que pueda valorar las posibles
deficiencias existentes en el diseño pseudoestático. Para presas de baja altura
o presas pequeñas en áreas no complejas, la Comisión recomienda el uso de
métodos convencionales pseudoestáticos, utilizando un coeficiente sísmico
horizontal constante que es seleccionado sobre una base de sismicidad de la
zona donde se encuentra la presa. Sin embargo, se han reconocido y demostrado
las insuficiencias de este enfoque pseudoestático para predecir el
comportamiento de la presa durante sismos; es por ello que en la actualidad se
sugiere y recomienda que se realice un análisis dinámico más exhaustivo bajo
modelos en MEF. Por todo lo argumentado anteriormente, en este trabajo se
realiza la modelación de una presa de materiales sueltos bajo la acción de
cargas dinámicas mediante elementos finitos y a su vez por un método empírico
propuesto por Makdisi y Seed, de los cuales se presenta un análisis y una
comparación del comportamiento de la presa.
Palabras
Clave – Presa de
material suelto, sismo, acción dinámica, metodo de elementos finitos
The International
Commission on Large Dams (ICOLD) recommends an approach to dynamic analysis in
which it indicates that dams should be designed by the conventional method
first, followed by a dynamic analysis that can assess possible deficiencies in
the pseudostatic design. For low head dams or small dams in non-complex areas,
the Commission recommends the use of conventional pseudostatic methods, using a
constant horizontal seismic coefficient that is selected on the basis of the
seismicity of the area where the dam is located. However, the inadequacies of
this pseudo-static approach for predicting dam behavior during earthquakes have
been recognized and demonstrated; that is why it is currently suggested and
recommended that a more exhaustive dynamic analysis be carried out under FEM
models. For all the above reasons, in this work the modeling of a dam of loose
materials under the action of dynamic loads is carried out by means of finite
elements and in turn by an empirical method proposed by Makdisi and Seed, from
which an analysis and a comparison of the dam behavior is presented.
Keywords - dam, seismic, dynamic action, finite element method
1.
Introducción
Las presas de materiales
sueltos constituyen obras hidráulicas y comúnmente se encuentra solicitadas por
diferentes acciones, entre ellas las dinámicas. Los métodos más comunes
utilizados en el análisis sísmico de la estabilidad de presas de tierra y enrocado
son los métodos pseudo-estáticos de equilibrio límite [1,2]. Estos métodos
consideran a la acción sísmica mediante una fuerza horizontal proporcional al
peso de la masa deslizante. Por otro lado, Makdisi y Seed (1978, [1])
propusieron un método de análisis para predecir los desplazamientos permanentes
de las presas sometidas a acciones sísmicas y sugirieron un criterio de
desempeño en oposición al concepto de utilizar un factor de seguridad basado en
los principios de equilibrio límite. El método es muy utilizado en la actualidad
por varios autores. [3-9]
Del estudio de terraplenes
durante sismos fuertes, se pueden discernir dos tipos distintos de
comportamientos: (1) el asociado con terraplenes arenosos de densos a medianos,
susceptibles a incrementos rápidos en la presión de poro debido al efecto de
las cargas cíclicas que resulta con el desarrollo de presiones de poros iguales
a la presión de efectiva sometida los cuales generan una disminución de la
resistencia la corte y potencial licuación. (2) el comportamiento asociado con
arcillas cohesivas compactadas, arenas secas y algunas arenas densas; el
desarrollo de de presiones de poro es mucho menor que el asociado con arenas
sueltas a densas medias, las cargas cíclicas resultantes son generalmente
bastante pequeñas, y el material retiene la mayor parte de su resistencia al corte.
(resistencia no drenada)
El enfoque de análisis
dinámico es recomendado por el Comité de Terremotos de la Comisión
Internacional de Grandes Presas: "las presas de terraplén altas mayores a
20 metros cuya falla puede causar pérdida de vida o daños mayores deben diseñarse
primero con el método convencional, seguido por un análisis dinámico para
investigar cualquier deficiencia que pueda existir en el diseño pseudo-estático
de la presa". Para presas bajas en áreas remotas, el Comité recomendó el uso
de métodos pseudoestáticos convencionales utilizando un coeficiente sísmico
horizontal constante seleccionado sobre la base de la sismicidad del área. Sin
embargo, la inadecuación del enfoque pseudoestático para predecir el
comportamiento de los terraplenes durante los sismos ha sido claramente
reconocida y demostrada. Además, en el mismo informe, la Comisión se refiere al
método convencional de la siguiente manera: "Existe una necesidad de una
revisión temprana del método convencional ya que los resultados del análisis
dinámico, las pruebas modelo y las observaciones de presas existentes muestran
que las aceleraciones horizontales debidas a las fuerzas sísmicas varían a lo
largo de la altura de la presa” [10]. Por lo tanto, en este artículo se compara
el comportamiento dinámico de una presa de materiales sueltos mediante el
método de elementos finitos y el análisis simplificado para determinar las
discrepancias del método y de la afirmación realizada por el ICOLD [2,3]
2.
Procedimiento aproximado
para el cálculo de la aceleración máxima
El método de Makdisi y Seed
(1978) es muy utilizado para calcular el periodo de vibración y aceleración
máxima en la cresta de presas de materiales sueltos, de esa manera es posible
determinar el máximo desplazamiento. A continuación, se realiza una breve
descripción del método.
2.1.
Evaluación
de propiedades iniciales
Si consideramos una presa
con altura H, velocidad de onda de corte Vs y una densidad de masa ρ,
y se asume que la sección es homogénea y de longitud infinita. El módulo de
corte máximo, Gmax, se relaciona a la velocidad de ondas de
corte, Vs, está dado por:
|
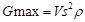
|
(1)
|
Para estimar la velocidad
de propagación de onda La curva de degradación indica la variación
Para la primera iteración
de cálculo se asume cualquier valor inicial de G, y se determina la relación
G/Gmax.
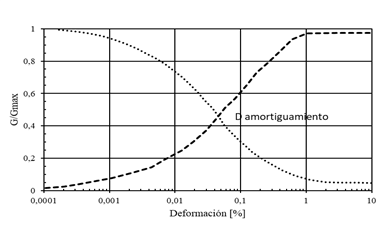
De la Fig. 1, se determina
los valores de deformación por cortante γav y amortiguamiento D.
Fig. 1. Módulo
de corte y amortiguamiento usado en las respuestas computacionales.
2.2.
Cálculo de la aceleración
máxima y el período natural
La aceleración máxima
según la teoría de la rebanada de corte, se calcula de la siguiente manera:
|
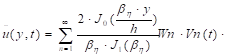
|
(2)
|
Dónde: Jo,
J1 = funciones Bessel de primera clase de orden cero y uno, βn
= el valor cero de la ecuación de frecuencia (wn /G) = 0 Jo
ρ, Wn= βn Vs /h,
donde Vs = G/ρ = frecuencia natural del modo nésimo.
|
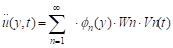
|
(3)
|
|
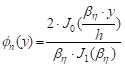
|
(4)
|
Considerando los tres
primeros modos de vibración, los valores correspondientes a βn
son siempre; β1 = 2.4, β2 = 5.25,
β3 = 8.65 y los valores correspondientes de las primeras
frecuencias naturales son:
|
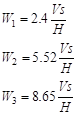
|
(5)
|
En la corona de la presa,
y = 0 y los valores correspondientes de los factores de participación modal
φn (0) para los tres primeros modos están dados por:
|
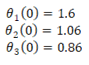
|
(6)
|
El valor de la aceleración
en la corona para cada modo está dado por la expresión:
|
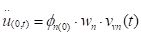
|
(7)
|
y el valor máximo de la
aceleración de la corona en cada modo está dado por:
|
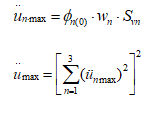
|
(8)
|
Donde: Svn, conocido
como velocidad espectral, es el valor máximo de Vn (t), y es
función de Wn, λn y las
características del movimiento del terreno üg(t). Para valores pequeños
de λn, la aceleración espectral es aproximadamente igual a Wn
Snv, por lo que la expresión para la aceleración máxima en la corona para cada
modo puede escribirse como:
|
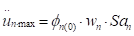
|
(9)
|
La aceleración máxima en
la corona para los tres primeros modos está dada por:
|
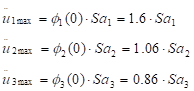
|
(10)
|
Como los valores máximos en
cada modo ocurren a diferentes tiempos, los valores máximos de la aceleración
de la corona se determinan por la raíz cuadrada de la suma de cuadrados de las
aceleraciones máximas de los tres primeros modos, luego:
|
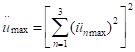
|
(11)
|
Para estimar la deformación
compatible con las propiedades del material, debe determinarse una expresión
para la deformación cortante promedio en la sección total. De la teoría de
rebanadas de corte, la expresión para la deformación cortante a cualquier nivel
en el terraplén como función del tiempo está dada por:
|
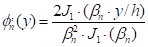
|
(12)
|
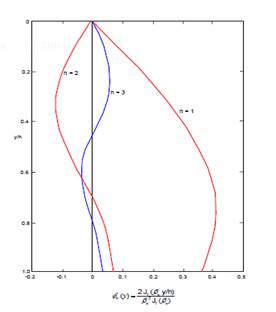
La Fig. 2 muestra la variación
de φ'n con la profundidad para los tres primeros modos. Considerando las
contribuciones pequeñas de los modos altos comparadas con el primer modo en
toda la profundidad, es suficiente para propósitos prácticos, considerar la
contribución de solo el primer modo en el cálculo de la deformación cortante
promedio. Por lo tanto, de la ec. 13, la expresión para la deformación cortante
máxima a cualquier nivel, y, puede escribirse como:
|
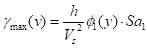
|
(13)
|
Donde φ'1 es el factor
de participación del primer modo, como se muestra en la Fig 2 y 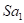 es la aceleración espectral que
corresponde a la primera frecuencia natural W1. La deformación cortante máxima
promedio para la sección total puede determinarse mediante el cálculo de un
valor promedio (φ'1) ave del primer factor de participación modal en la
Fig. 2:
es la aceleración espectral que
corresponde a la primera frecuencia natural W1. La deformación cortante máxima
promedio para la sección total puede determinarse mediante el cálculo de un
valor promedio (φ'1) ave del primer factor de participación modal en la
Fig. 2:
Fig. 2. Variación
de factores de participación modal de deformación cortante con profundidad –
teoria- de rebanada de corte.
3.
Materiales y métodos
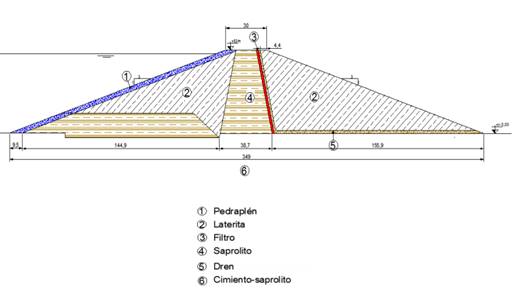
El perfil en el cual se
realizó el presente estudio es una estructura de materiales sueltos tipo
homogéneo con un dren chimenea vertical (Figura 3). La altura prevista de la
presa es de 53 m en su construcción final, la cual se realizará en tres fases.
El ancho de coronamiento es de 30 m, que serán suficientes para el paso de
vehículos y/o alguna infraestructura auxiliar para el transporte de los
relaves. El nivel de nominal de embalse es de 48 m sobre el terreno natural, de
esta manera, se tendrá 5 m de revancha como seguridad. La geometría de la presa
queda definida por un talud de agua arriba 1:3 y talud de aguas abajo 1:3. El
cuerpo de la presa está conformado por lateritas compactadas a densidad Proctor
Modificado. El Núcleo impermeable es de saprolito que se encuentra a pocos
metros de profundidad. Cuenta con filtro-dren chimenea y para controlar el
flujo de filtraciones por el cuerpo de la presa, de manera que el espaldón de
aguas abajo permanezca seco. La protección del talud de agua arriba será por
medio de Rip Rap, apoyado sobre una transición de escollera.
3.1.
Materiales
utilizados
La Tabla 1 muestra las
propiedades físicas, mecánicas e hidráulicas de los materiales que constituyen
los diferentes materiales. El modelo constitutivo utilizados para los materiales
es el de Mohr-Coulomb. Para la determinación del mismo es necesario dos
parámetros, la cohesión (c) y el ángulo de fricción interna (ϕ).
El criterio de fluencia de Morh-Culomb consiste en seis funciones de fluencias,
las cuales representadas en un espacio tridimensional σ1,
σ2 y σ3.
Tabla 1. Propiedades físicas, mecánicas e
hidráulicas de los materiales que constituyen la presa. Tomadas de [11]
|
Material
|
γd
|
γsat
|
K
|
c
|
ϕ °
|
C
|
E
|
μ
|
ψ
|
|
|
kN/m3
|
kN/m3
|
[m/día]
|
kPa
|
|
|
kN/m2
|
|
°
|
|
1 Pedraplén
|
18
|
20
|
1
|
1
|
35
|
D
|
30000
|
0.3
|
No
|
|
2 Suelo lateritico
|
16
|
19
|
0.08
|
20
|
10
|
ND
|
50000
|
0.35
|
No
|
|
3 Arena
|
16.5
|
18
|
1
|
1
|
32
|
D
|
20000
|
0.30
|
34
|
|
4 Saprolito
|
13
|
15
|
8.6E-5
|
2
|
28
|
ND
|
240000
|
0.35
|
No
|
|
5 Dren
|
16
|
17.4
|
1
|
1
|
33
|
D
|
20000
|
0.3
|
34
|
|
6 Saprolito Compactado
|
14.5
|
16
|
8.6E-5
|
15
|
18
|
ND
|
250000
|
0.35
|
No
|
Donde γd = densidad del
suelo seco, γsat = densidad del suelo
saturado, K= permeabilidad, c = cohesión,
ϕ = ángulo de
fricción interna, C = Comportamiento, D = Drenado, ND = No drenado, E = módulo
de elasticidad, μ = Poisson, ψ = ángulo de dilatancia
Fig. 3 Esquema de modelacion de la presa de materiales suelta
3.2.
Modelación mediante el
método de elementos finitos
Para comparar los resultados
obtenidos del método de empírico, se realizó un modelo numérico empleando el método
de los elementos finitos. El mallado de la geometría del modelo fue constituida
por elementos triangulares de 15 nodos, los cuales proporciona una
interpolación de cuarto orden para los desplazamientos y la integración
numérica. El mallado en general posee una malla de tamaño grueso y en donde
existía una posible concentración de tensiones se optó por una malla más fina.
La ecuación básica del comportamiento dinámico es la siguiente [14]
|
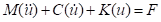
|
(14)
|
En donde M= matriz de
masa, C= matriz de amortiguamiento, K=matriz de rigidez, u
desplazamiento, u la aceleración y u la velocidad, y F el vector de cargas.
En la matriz M, se consideró
la masa de los materiales (suelo + agua). La matriz C representa el amortiguamiento
de los materiales. Si se supone un comportamiento elástico, el amortiguamiento todavía
puede tenerse en cuenta en el uso de la matriz C. Para determinar la matriz de
amortiguamiento, se requieren parámetros adicionales, que son difíciles de
determinar a partir de pruebas. En las formulaciones de elementos finitos, C se
fórmula a menudo como una función de la masa.
3.3.
Calibración del modelo de
elementos finitos
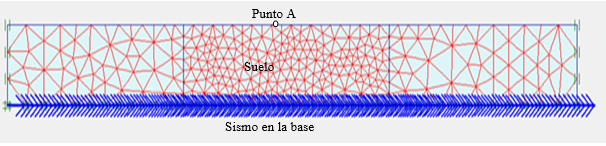
Para realizar la modelación
en elementos finitos se discretizó la zona de influencia con un mallado más
fino (Fig. 5). Con el fin de verificar si el mallado es el adecuado, se realizó
una comparacion de las deformaciones obtenidas mediante el método de elementos finitos
y la función de transferencia para un estrato homogéneo. Se aplicó el modelo
con un ruido blanco aleatorio en el borde con el fin de obtener las frecuencias
fundamentales. En la Figura 4 se indica el modelo de validación y la Fig. 5 el
ruido blanco con el cual se obtuvieron los resultados. La Fig 6 corresponde a
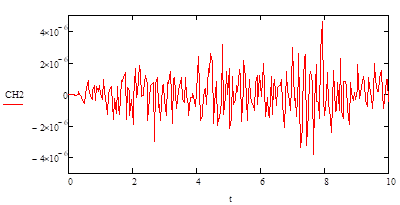
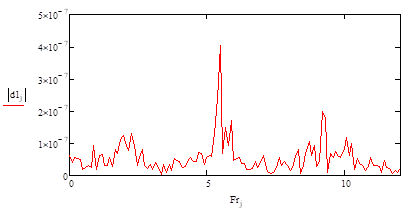
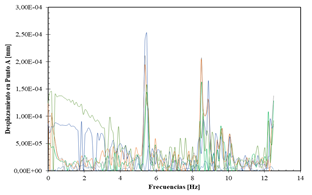
los desplazamientos en el punto A y la Fig. 7 es la transformada de Fourier de
los desplazamientos en A, donde se observa una frecuencia mayor en los 5.5 Hz
Fig. 4
Mallado del modelo de Validación.
Fig. 5 Ruido
blanco aleatorio considerado en el model numérico( fuente propia).
Fig. 6. Desplazamientos parte superior (punto A).
Fig. 7. Transformada
de Fourier de desplazamientos. (punto A).
3.4.
Calculo de la función de
transferencia.
Considerando un estrato homogéneo la función de transferencia, se
relaciona con el periodo, velocidad de propagación y la altura del estrato de
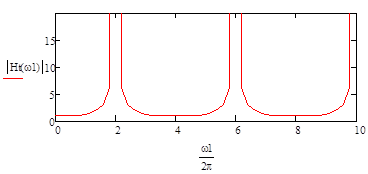
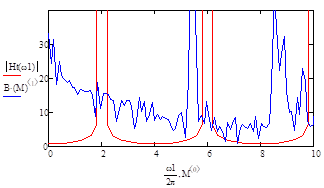
la siguiente manera, considerando, r =1850 kg/m3, Vs=399 m/s, H=50m. En la Fig 8, se muestra la función de
transferencia para el estrato homogéneo y la comparación obtenidas por el MEF y
función descripta, se obtuvieron amplitudes muy similares en coincidente en la
frecuencia con respecto a la Fig .7
|
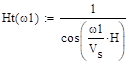
|
(15)
|
|
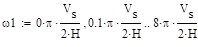
|
(16)
|
Fig. 8. Función
de transferencia estrato homogéneo.
Fig. 9. Comparación.
3.5.
Calibración del modelo de
elementos finitos
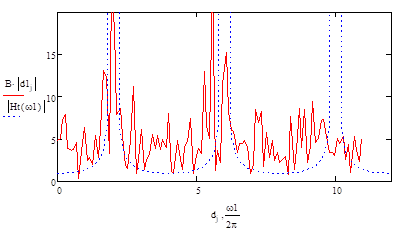
La Fig. 10 la variación del desplazamiento del punto A en función de la
Frecuencia para diferentes ruidos blancos. Los resultados indican que el
mallado realizado se ajusta a los resultados. A continuación, se probaron una
serie de ruidos blancos aleatorios para determinar una mayor precisión de los
resultados. Posteriormente, se calculó el promedio, donde se indica un ajuste
medio con la función de transferencia del estrato homogéneo. La Fig. 11 indica
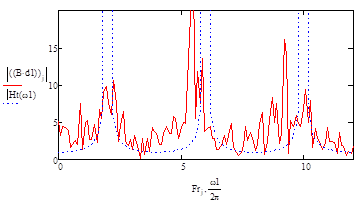
un ajuste considerable si disminuimos los ruidos blancos a un tercio.
Fig. 10. Comparación
diferentes ruidos blancos.
Fig. 11. Promedio
de ruidos blancos.
Fig. 12. Un
tercio del ruido blanco. (indica un ajuste considerable si disminuimos los
ruidos blancos a un tercio).
3.6.
Sismo utilizado para las
modelaciones
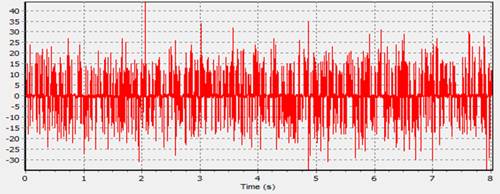
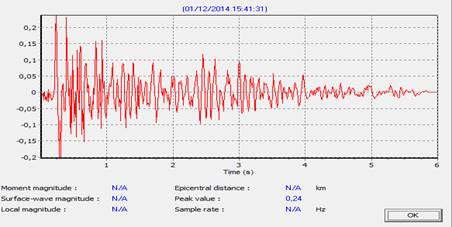
El sismo utilizado para excitación es el denominado
“el centro” [12]. El terremoto de “el Centro de 1940” ocurrió a las 21:35 hora
del Pacífico el 18 de mayo (05:35 UTC del 19 de mayo) en el Valle Imperial en
el sureste de California, cerca de la frontera internacional de los Estados
Unidos y México. Tenía una magnitud de momento de 6.9 y una intensidad máxima (Extremo)
en la escala de intensidad de Mercalli. Fue el primer gran terremoto registrado
por un sismógrafo de movimiento fuerte ubicado junto a una ruptura de falla.
Este sismo se fue ampliamente utilizado para el diseño y estudio, de varios
acontecimientos. [12]
Fig. 13. diagrama
de aceleraciones sismos el centro.
4.
Resultados y análisis
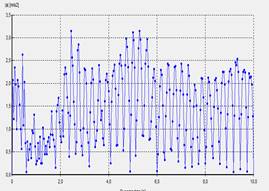
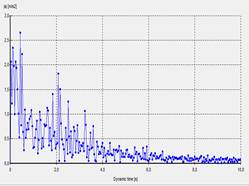
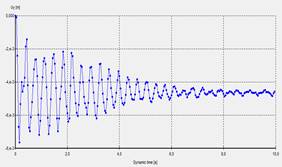
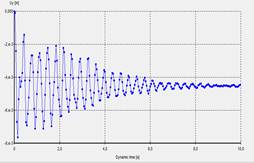
La Fig.14 muestra los resultados obtenidos del modelo
numérico. Aquí se muestran los resultados de deformaciones obtenidas en la
cresta de la presa analizada, para la aceleración total (Fig. 14a) y para un
tercio de las mismas (Fig. 14b). Al igual que las deformaciones alcanzadas. En
las deformaciones encontradas se notan la caída de la misma debido al
amortiguamiento del material, en este caso el suelo.
En la Tabla 2 muestra los resultados obtenidos a
partir del Método de los Elementos Finitos y el método propuesto por Makdisi y
Seed (1974). Los resultados revelan que las aceleraciones máximas obtenidas son
mayores por el método de Makdisi y Seed [1] que por el método de elementos
finitos. Lo mismo ocurre con el período de vibración. Es decir, el método [1]
tiende a subestimar los valores de comportamiento de aceleración máxima y
período de vibración. Si bien los valores son del orden, se indica que el
método es valioso debido a la facilidad que se tiene en obtener los resultados,
dado que MEF posee un gasto en simulación elevado y costoso. Teniendo cuenta
estos resultados, es considerable poder realizar las dos comparaciones. En
cuanto al MEF, es una herramienta muy potente y sofisticada la cual es posible
tener parámetros en todos los puntos del sistema.
Tabla 2 Comparación de resultados obtenidos por MEF y Makdisi y Seed (1978)
|
Resultados
|
MEF
|
Makdisi
y Seed (1978)
|
|
a max
|
0.25g
|
0.27g
|
|
T0
|
0.40
seg
|
0.42
seg
|
|
Aceleración total sismo total
|
Aceleración total 1/3
sismo
|
|
|
|
|
Desplazamientos sismo y
|
Desplazamientos sismo y
con 1/3 amplitud
|
|
|
|
Fig. 14. Deformaciones
obtenidas en la cresta de la presa (a) Aceleración total, sismo total, (b)
Aceleración total 1/3 sismo, (c) Desplazamiento sismo y, (d) Desplazamiento
sismo y con 1/3 amplitud.
5.
Conclusiones
Las modelaciones de una presa
de materiales sueltos vía método de elementos finitos, exige la implementación
de un mallado y condiciones de bordes adecuados para que los resultados sean
los correctos, el mallado debe ser tal que se obtenga un menor costo
computacional. Para este caso particular, los ruidos blancos modelados se
correlacionaron en gran manera con la función de transferencia de un medio
homogéneo.
Las aceleraciones máximas
obtenidas por el método de Makdisi y Seed (1974), son mayores que mediante el
análisis del método de elementos finitos para amplitudes de sismos mayores,
como el caso del sismo “El centro”. Para el caso de sismo de menores amplitudes
(ejemplo, un tercio de la amplitud del centro) las aceleraciones coinciden
satisfactoriamente.
6.
Referencias
|
[1]
|
Makdisi, F, y H Seed. «Simplified procedure dam and embankment
earthquake-induced deformations.» Journal of geotechnical Engineering, 1978.
|
|
[2]
|
Martínez, Rafael, Barrera, Sergio, & Gómez, Patricio. (2011). El
método seudoestático de estabilidad en presas: un análisis crítico. Obras y proyectos, (9), 30-37.
https://dx.doi.org/10.4067/S0718-28132011000100004
|
|
[3]
|
Barkhordari, K., & Entezari Zarch, H. (2015). Prediction of permanent
earthquake-induced deformation in earth dams and embankments using artificial
neural networks. Civil engineering infrastructures journal, 48(2), 271-283.
|
|
[4]
|
Esfahani Kan, M., Taiebat, H., & Taiebat, M. A framework to
assess Newmark-type simplified methods for evaluation of earthquake-induced
deformation of embankments.
|
|
[5]
|
Veylon, G., Luu, L. H., Mercklé, S., Bard, P. Y., Delvallée, A.,
Carvajal, C., & Frigo, B. (2017). A simplified method for estimating
Newmark displacements of mountain reservoirs. Soil Dynamics and Earthquake
Engineering, 100, 518-528.
|
|
[6]
|
Luu, L. H., Veylon, G., Mercklé, S., Carvajal, C., & Bard, P. Y.
(2018). A simplified
method for estimating seismic performance of small homogeneous earth dams. In
Validation of Dynamic Analyses of Dams and Their Equipment (pp. 247-254). CRC Press.
|
|
[7]
|
Laguardia, R., Gallese, D., Gigliotti, R., & Callisto, L. (2020).
A non-linear static
approach for the prediction of earthquake-induced deformation of geotechnical
systems. Bulletin of
Earthquake Engineering, 18(15), 6607-6627.
|
|
[8]
|
Durmaz, S., & Ülgen, D. (2021). Prediction of earthquake-induced
permanent deformations for concrete-faced rockfill dams. Natural Hazards, 105, 587-610.
|
|
[9]
|
Jafarian, Y., & Lashgari, A. (2016). Simplified procedure for
coupled seismic sliding movement of slopes using displacement-based critical
acceleration. International Journal of Geomechanics, 16(4), 04015101.
|
|
[10]
|
Bowles, D. S., Giuliani, F. L., Hartford, D. N., Janssen, J. P. F.
M., McGrath, S., Poupart, M., ... & Zielinski, P. A. (2007). ICOLD
bulletin on dam safety management. IPENZ Proceedings of Technical Groups,
33(2).
|
|
[11]
|
Bogado, G. O., Reinert, H. O., & Francisca, F. M. (2019). Geotechnical properties of residual
soils from the North-east of Argentina. International Journal of Geotechnical Engineering,
13(2), 112-121.
|
|
[12]
|
Kramer,
S. Geotechnical Earthquake Engineering. Prentice Hall, 1996.
|