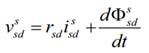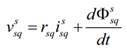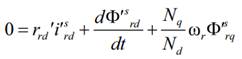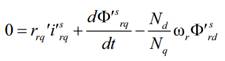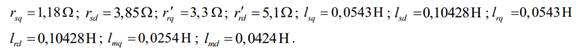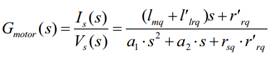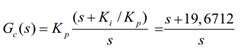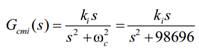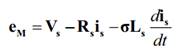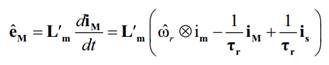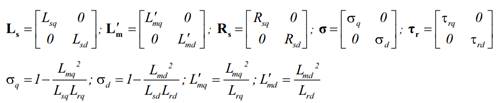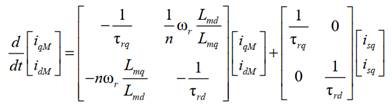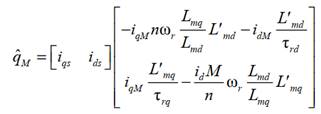1.
Introducción
El presente trabajo surge del análisis y de una
demanda concreta del ámbito rural, más específicamente de la provincia de
Misiones, Argentina. Dichas zonas generalmente se encuentran alejadas de las
redes de energía eléctrica y distribución de agua, por lo que el costo de
instalación de líneas de distribución y estación transformadora, es elevado. En
este ambiente, es común que las personas busquen otras alternativas para
generar la energía eléctrica y la obtención del agua. En las zonas rurales,
dicha energía eléctrica tiene, entre otros usos, uno esencial que es el de
bombeo de agua tanto para uso personal como para riego de huertas.
Si bien la solución más común para habitantes de
comunidades pequeñas y/o aisladas, es obtener la energía eléctrica mediante
generadores impulsados con motores de combustibles fósiles, en las últimas
décadas se han realizado estudios que buscan proponer alternativas ecológicas y
sustentables. De tales alternativas, el uso de paneles solares para
alimentación de bombas de agua [1]-[3] es la que captó (y aún lo hace) mayor
atención como solución, debido a la amplia disponibilidad de radiación solar,
con más o menos intensidad, en todo el planeta. En dicha aplicación, dado que
el suministro de energía de los paneles no es constante, y de hecho puede
fluctuar notablemente durante el día, se debe buscar obtener la mayor
eficiencia posible a través de transferir a la bomba, la máxima potencia disponible
en la fuente. Es, por tanto, en la etapa de conversión y adaptación de energía
eléctrica, donde se ve la importancia del correcto control de la bomba de agua,
que actúa como carga del sistema de paneles. Este control de la potencia
entregada a la bomba, puede hacerse mediante técnicas de seguimiento del máximo
punto de potencia de los paneles solares (MPPT - Maximum Power Point Tracking)
[4]-[6] mediante convertidores electrónicos de potencia, cuyas topologías
dependen del tipo de bomba utilizada [7],[8]; de corriente continua (CC) o de
corriente alterna (CA). Otra forma de realizar el control de potencia de
bombeo, es almacenando primero la energía eléctrica producida por los paneles
en un banco de baterías y utilizarla luego, a través de convertidores
electrónicos de potencia para alimentar y controlar la bomba. Esta forma es muy
común cuando se usan bombas de CA, sean estas centrífugas o periféricas (por lo
general usadas en aplicaciones domésticas), siendo este tipo de bomba la
elegida para la presente propuesta [7]; dado su bajo costo y bajo mantenimiento
en relación con las bombas de CC [2].
En este trabajo se propone el control indirecto de
torque de una bomba centrífuga de CA, alimentada desde un banco de baterías
mediante un convertidor electrónico de potencia CC-CA, dichas bombas
generalmente constan de un motor monofásico y el cuerpo de la bomba, que se
acopla al eje. Debido a esto, se estudia y analiza el modelo de un motor
monofásico, y las diferentes estrategias de control utilizadas actualmente,
conjuntamente con su costo y dificultad de implementación [9].
Dependiendo de la topología usada [10], se puede
controlar la bomba con un inversor monofásico, controlando un solo voltaje de
salida que alimenta a ambos bobinados del motor monofásico (en cuyo caso se
necesita una llave centrífuga o un capacitor permanente), o, se puede tratar el
motor como una máquina de dos fases, controlando el voltaje aplicado a cada
bobinado por separado, utilizando un inversor trifásico. Como es de esperarse,
al ir del sistema más simple al más complejo, se obtiene mayor facilidad para
controlar diferentes parámetros del funcionamiento, como puede ser velocidad y
torque por separado. Por otro lado, se presenta un aumento de componentes, y,
por lo tanto, del costo total del equipamiento y del mantenimiento. Se debe
buscar entonces una relación de compromiso, considerando que la solución
demandada debe reducir los costos y resultar confiable.
Para plantear una relación de compromiso razonable, se
han analizado las estrategias de control más comunes para motores monofásicos y
las topologías de conversión necesarias en cada caso. Entre ellas se encuentra
el Control de Flujo Orientado Indirecto, o IFOC (del inglés Indirect Flux
Oriented Control), mostrada en [11], siendo necesario para implementar esta
estrategia, un inversor de dos fases. Este método permite el control por un
lado del flujo magnético, y por el otro, del torque eléctrico y velocidad del
motor, por medio de las corrientes de estator, sin embargo, presenta el inconveniente
de necesitar, además de sensores de voltaje y corriente para cada bobinado, un
sensor de velocidad, puesto que se necesita tanto la velocidad, como una
estimación del módulo y ángulo del flujo rotórico.
Por otra parte, otra estrategia común es el Control
Directo de Torque, o DTC (del inglés Direct Torque Control), visto en
[12]. Como su nombre lo indica, permite controlar el torque directamente, cambiando
el ángulo entre el vector de voltaje aplicado al motor y el vector de flujo de
estator. Al igual que IFOC, utiliza un inversor de dos fases. Tiene la ventaja
de no necesitar medición de velocidad, y el control del inversor se realiza con
un simple control por histéresis. Sin embargo, aún necesita estimación del
flujo por medio de medición de voltajes y corrientes de los bobinados del motor,
la cual resulta sensible a la variación de parámetros del motor, o más
específicamente, según la estimación propuesta en [12], de la resistencia de
estator. Además, no permite control de corriente, lo que sí es posible con IFOC.
Si bien ambas técnicas de control tienen sus ventajas
y desventajas. Ambas comparten el hecho de que se necesita un inversor de dos
fases, que, como ya se mencionó, aumenta la complejidad y el costo al momento
de implementar un sistema. Es debido a estos aspectos de la implementación, que
surge el objetivo de este trabajo, y el cual propone utilizar una técnica de
control de torque indirecto (derivada del IFOC) que permita obtener un buen
desempeño transitorio, utilizando apenas un inversor monofásico; todo esto
midiendo la tensión y corriente en el bobinado principal, sin necesidad de
utilizar un sensor de velocidad, el cual incrementa costos y modificaciones en
la máquina para su inserción.
Para ello, partiendo del modelo de un motor
monofásico, se propone y diseña un sistema de control con un lazo interno de
corriente, que controla la corriente del bobinado primario del motor, y, por medio
de la misma, el torque, y un lazo externo que controla la velocidad del mismo
motor. Para el lazo interno de corriente, se propone utilizar, con el objetivo
de realizar un análisis comparativo de desempeño, dos controladores clásicos:
un controlador PI y un resonante.
La velocidad se estima por medio de un algoritmo de
modelo de referencia adaptativo o MRAS (del inglés Model-Reference
Adaptative System) [9]. Dicho método de estimación utiliza dos modelos, uno
de referencia y uno adaptativo, que tienen como entrada las tensiones y
corrientes medidas en ambos bobinados del motor, para generar una velocidad
estimada u “observada”. Se considera este algoritmo puesto que generalmente es
más conveniente medir tensión y corriente que medir velocidad del motor, debido
a las modificaciones físicas necesarias para la instalación de un sensor de
velocidad y el costo que el mismo conlleva. Por lo tanto, la propuesta concreta
de este trabajo, se basa en una estrategia de control indirecto de torque,
mediante un lazo interno de control de la corriente del bobinado primario, y un
lazo externo de control de velocidad, utilizado un estimador adaptativo robusto
para generar la referencia de corriente. Además, se realiza en este trabajo, un
análisis comparativo de desempeño del control indirecto de torque, mediante la
utilización de dos controladores clásicos en el control de la corriente: un PI
y un resonante.
La propuesta que aquí se presenta, es corroborada
mediante resultados de simulación, los cuales demuestran que mediante una
solución sencilla pueden conseguirse resultados con desempeños satisfactorios
para la aplicación de bombeo requerida.
2. Descripción del sistema de bombeo y de control de
la bomba
2.1. Microrred eléctrica para la alimentación de
bombas e iluminación
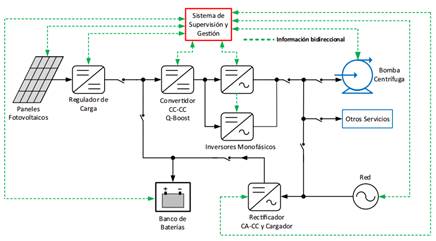
El desarrollo que aquí se expone, es parte esencial de
un proyecto PDTS (Proyecto de Desarrollo Tecnológico y Social), de “Bombeo de
agua con energías renovables, almacenamiento de energía y conexión a la red
para pequeñas huertas rurales comunitarias”, del cual se presenta el esquema completo
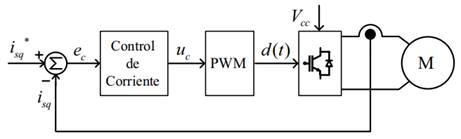
en la Fig. 1. En este esquema, el control de la bomba centrífuga mediante el
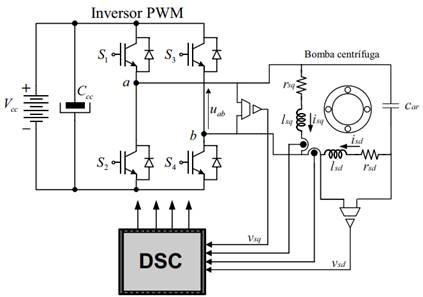
inversor monofásico, es la parte que concierne a este artículo. El circuito
eléctrico de conversión de energía para alimentar la bomba, que se utilizará en
el presente análisis, está conformado, por lo tanto, por un inversor monofásico
PWM alimentado en tensión desde un banco de baterías, a través de un convertidor
elevador Quadratic-boost. El circuito de control de la bomba, utilizando
un inversor monofásico de puente completo se muestra en la Fig. 2.
Fig.
1. Microrred eléctrica de generación propuesta para bombeo de agua utilizando
energía solar fotovoltaica.
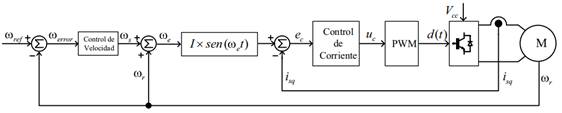
Fig.
2. Esquema de control de la bomba centrífuga.
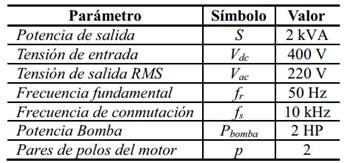
En la Tabla 1 se muestran los parámetros del inversor
y de la bomba a controlar; los parámetros de la bomba se obtuvieron de [9].
Tabla
1. Parámetros del inversor monofásico y de la bomba
El inversor mantiene la frecuencia de conmutación
constante, mientras que el sistema de control modifica el ciclo de trabajo de
las acciones PWM, para sintetizar una sinusoidal de amplitud y frecuencia
variable que alimenta tanto el bobinado principal del motor, como el bobinado
secundario, conectado con un capacitor permanente que permite el arranque.
De la bomba se miden los voltajes y corrientes de ambos
bobinados, que se realimentan al controlador para la realización de la
estrategia de control a lazo cerrado, la cual se desarrolla en las siguientes
secciones. La propuesta es implementar dicha estrategia en un Controlador
Digital de Señales (DSC), el cual se observa en la Fig. 2, no obstante, la
validación experimental se realizará en una segunda etapa.
2.2. Modelo del Motor de Inducción Monofásico
2.2.1. Modelo eléctrico:
Un motor monofásico consta de dos bobinados, uno
primario que recibe el voltaje de alimentación en su totalidad, y es el
encargado de generar el torque eléctrico para mover cualquier carga en el eje (en
este caso, la bomba), y uno auxiliar, que actúa para dar un torque de arranque,
de forma que el eje pueda moverse sin necesidad de un pulso de torque externo.
Este bobinado auxiliar tiene varias formas de conectarse, como se presentan en
[9], entre ellas, el uso de una llave centrífuga para que el mismo solo actúe
durante el arranque, con o sin un capacitor de arranque que ayuda en el
desfasaje de la corriente sobre el bobinado, o una forma más común, usando un
capacitor permanente.
Se presenta el modelo de motor de jaula de ardilla (es
decir, los voltajes de rotor están cortocircuitados), obtenido de [9],
siguiendo el esquema eléctrico de la Fig. 3. Para aplicar este modelo a un
motor de jaula de ardilla comercial, se considera que el eje “q” se
corresponde con el bobinado principal, mientras que el eje “d” se corresponde
con el auxiliar.
Fig.
3. Circuito eléctrico equivalente del modelo de un motor monofásico [9].
Para este modelo se toman las siguientes
consideraciones:
• El entrehierro entre rotor y estator es uniforme.
• Las ranuras de estator están uniformemente
distribuidas.
• Las resistencias de los bobinados no varían con la
temperatura y se desprecia el efecto skin.
Siguiendo esto, las ecuaciones de voltaje estatórico
están dadas por:
|
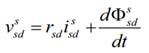
|
(1)
|
|
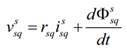
|
(2)
|
Donde el superíndice “s” indica que las magnitudes
usan un marco de referencia en el estator, rsd y rsq se
corresponden a las resistencias estatóricas, Φ ssd y Φ ssq
a los flujos estatóricos, y vssd, vssq,
issd e issq, son los voltajes y corrientes
estatóricas respectivamente.
Se presentan, además, las ecuaciones del rotor, siendo
todas las magnitudes con apóstrofe referenciadas al estator usando la relación
de vueltas entre estator y rotor.
|
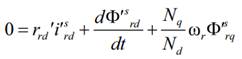
|
(3)
|
|
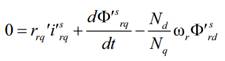
|
(4)
|
Las ecuaciones de
flujo están dadas por:
Siendo:
Para el motor
utilizado en la simulación, los parámetros toman los siguientes valores [9]:
El torque
eléctrico generado en el motor está dado por:
|
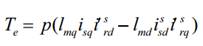
|
(9)
|
2.2.2. Modelo
mecánico
Partiendo de la
ecuación del torque en el eje, se tiene que:
|
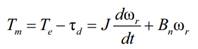
|
(10)
|
Donde Tm
es el torque mecánico, τd es un disturbio en el torque, J es el
momento de inercia, Bn es el coeficiente de fricción y ωr la
velocidad del rotor. En el caso del motor simulado, J=9.10 -4 kg.m2,
y Bn se considera nulo.
3. Estrategia de
Control
3.1. Diseño del
Lazo de Control de Corriente (Control Indirecto de Torque)
El objetivo del
lazo de control de corriente es controlar de forma indirecta el torque eléctrico
disponible en el motor de la bomba. Sin embargo, a diferencia del control
presentado en [11], el cual utiliza un inversor de tres brazos para poder
controlar la corriente en ambos bobinados, se busca utilizar un inversor
monofásico de dos brazos, por lo que no será posible realizar un control para,
por ejemplo, mejorar el arranque de la bomba. En este sentido, es importante
aclarar que esta estrategia puede ser útil para bombas de potencias bajas y
teniéndose en cuenta un factor de seguridad en el dimensionamiento de los
semiconductores del inversor, en cuanto a las solicitaciones de corriente durante
el arranque, como así también una estrategia de limitación de corriente para
operación con sobrecarga, si fuera necesario.
El análisis del
control de corriente en el bobinado principal se divide en dos secciones. La
primera se realiza alimentando con el inversor solamente dicho bobinado,
utilizando un torque externo para que el rotor comience a girar. Y la segunda,
una vez validado el sistema de control de corriente, consiste en conectar el
bobinado secundario con un capacitor de arranque fijo, considerando cualquier interacción
de la corriente del mismo con la del primario como una perturbación que el
sistema de control debe suprimir o atenuar.
En la Fig. 3 se
observa que con rotor bloqueado el circuito del bobinado principal se reduce a
un circuito RL, cuya función de transferencia (FT) de corriente Is(s)
en función de voltaje de estator Vs(s) en el plano de Laplace está
dada por la siguiente expresión:
|
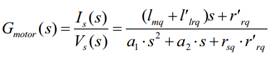
|
(11)
|
Donde:
Reemplazando los
valores de los parámetros del motor usado, se obtiene la siguiente FT:
|
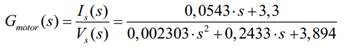
|
(12)
|
Como se mencionó
anteriormente, se propone utilizar esta función de transferencia para el
control de corriente del bobinado principal del motor, suponiendo en un
principio que cualquier interacción del bobinado secundario por inducción de
tensión se considera una perturbación que el sistema de control debe
contrarrestar. Se analizará el desempeño del sistema de control para verificar
si dicha suposición es viable.
A su vez, el
motor se controla con un inversor PWM, con una tensión de entrada de corriente continua
de 450 V. Teniendo en cuenta que dicho valor se presenta a la salida con un
ciclo de trabajo PWM normalizado entre 0 y 1 (valores en p.u.), y considerando
que la frecuencia de la señal PWM aplicada al motor es mucho mayor que la
frecuencia de la señal controlada, se puede considerar la ganancia del actuador
como un valor constante durante un periodo de actuación, Ka = 450 V.
Agregando dicha
ganancia del actuador a la FT del motor, se obtiene la siguiente FT de la
planta:
|

|
(13)
|
Los polos de la
(13) se encuentran en p1= -19,6712rad/s y p2= -85,9429rad/s
, mientras que el cero se encuentra en z1= -60,7735rad/s .
Como se planteó
inicialmente, se propone diseñar un controlador clásico PI y un controlador resonante,
para luego efectuar una comparación del desempeño de ambos. Para el diseño del controlador
PI, se elige una cancelación polo-cero, cancelando la dinámica más lenta de la
planta, es decir, el polo p1, y manteniendo la ganancia Kp
unitaria (la misma puede modificarse más adelante para mejorar la respuesta
transitoria del sistema hasta valores deseados). De este modo, la expresión del
controlador PI se presenta a continuación:
|
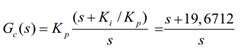
|
(14)
|
La Fig. 4
presenta un diagrama en bloques simplificado del sistema de control de
corriente:
Fig. 4 -
Lazo interno de control de corriente.
Como es bien
sabido, el control PI únicamente puede garantizar error nulo para entrada
constante o de frecuencia cero. Entonces, al ser la referencia de corriente,
que el inversor debe imponer al motor, una señal sinusoidal, la reducción del
error de régimen estacionario, únicamente se consigue con el incremento de la
ganancia del controlador y, por ende, de la ganancia del camino directo del
lazo de control. Sin embargo, el valor que tome la ganancia del controlador,
resultará de una solución de compromiso entre el valor del error, el desempeño
en régimen transitorio para mejorar el rechazo a perturbaciones y adecuados
márgenes de estabilidad relativa.
Con el objetivo
de poder llevar a cero el error de régimen estacionario, para la referencia mencionada,
es adecuado en función de lo que establece el Principio del Modelo Interno
(PMI), imponer en el camino directo, el denominador de los polos inestables de
la referencia. En este sentido, el controlador puede adoptar la siguiente
expresión:
|
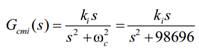
|
(15)
|
En la cual, ki,
permite ajustar la velocidad de convergencia del error de corriente a cero y
ωc se define de la siguiente forma: ωc = 2
π f1 (rad/s), siendo f1 = 50 Hz. Para
reducir las oscilaciones en el arranque y poder estabilizar rápidamente el lazo
debido a la presencia de los polos imaginarios de Gcmi(s), se suma
una acción proporcional Kpmi = 0,15.
Es importante
aclarar, que este controlador opera correctamente en régimen estacionario con velocidad
nominal, eliminando el error para la frecuencia selectiva ωc
para la cual se diseña, no así durante el transitorio de arranque del motor,
debido a la variación de frecuencia de la corriente durante este periodo. Para
eliminar el error durante el arranque de la bomba, debería adaptarse el valor
de la frecuencia ωc en función del deslizamiento, pero dado que
este no es un proceso que requiera error
nulo en el
arranque, puede despreciarse el error que se produce.
Es relevante
agregar también, que estos controladores basados en el PMI, resultan robustos
ante variaciones paramétricas, dado que garantizan un error nulo de seguimiento
a pesar de que resulte afectado el desempeño transitorio, haciendo que el
sistema sea siempre asintóticamente estable.
3.2. Lazo de
Control de Velocidad
Dado que la
aplicación deseada del control de motor estudiado es bombeo de agua, se puede suponer
en primera instancia que el caudal de agua saliente de la bomba será
proporcional a la velocidad angular del eje del motor. Por esto, una vez
validado por simulación el control de corriente, se analiza la posibilidad de
controlar dicha velocidad.
Teniendo en
cuenta que la velocidad máxima teórica del motor, o velocidad de sincronismo
está dada por:
|
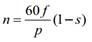
|
(16)
|
Donde “f”
es la frecuencia eléctrica, y “s” el deslizamiento.
La estrategia de
control más simple empleada usualmente es el control escalar, donde se mantiene
constante, la relación de voltaje de estator y frecuencia eléctrica Vs/f
a velocidades menores a la nominal del motor, y se varía solo la frecuencia a
velocidades mayores para mantener la potencia constante. Sin embargo, la
entrada del sistema es un voltaje sinusoidal entregado por el inversor, con la
expresión VAC (t) = Vpsen(2 πft) . Dicha señal tiene solo dos grados de libertad, el
voltaje Vp y la frecuencia f. Como el voltaje Vp
es controlado por la referencia de corriente, el control de velocidad se limita
al uso de la variable libre restante, la frecuencia eléctrica.
Se propone
entonces, un esquema en donde el lazo de control de velocidad afecta solamente
a la frecuencia de la corriente, manteniendo su valor de pico constante. De
este modo, dado que la velocidad de sincronismo es dependiente de la frecuencia
eléctrica, sería posible, dentro de ciertos límites, controlar la velocidad del
motor.
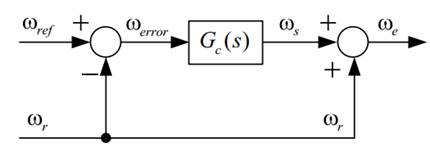
Fig. 5.
Esquema de control de velocidad.
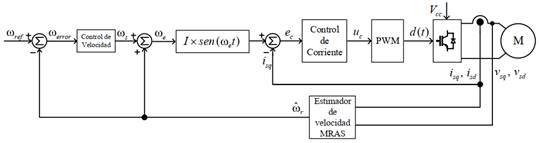
Como se mencionó
anteriormente, el control de velocidad se basa en una estrategia de control escalar.
El esquema de bloques de la Fig. 5 muestra el proceso para obtener la
frecuencia eléctrica que controla el inversor. Se parte de obtener el error,
ωerror, entre la frecuencia angular de referencia ωref
y la frecuencia angular (velocidad) del rotor del motor ωr.
Una vez obtenido
el valor de error, el mismo pasa por un controlador, del cual se obtiene la frecuencia
de deslizamiento ωs. Por último, para obtener la frecuencia
angular eléctrica, o frecuencia de sincronismo ωe, que
controlará el inversor, se suma ωs con ωr.
3.2.1. Control
con Medición de Velocidad
Para validar el
control de velocidad propuesto, en primera instancia, se procede a utilizar el
valor de velocidad medido. Dado que se trabaja con simulación, en este caso se
llama “valor medido” al valor obtenido de la simulación, el cual se calcula con
las ecuaciones (9) y (10). Para simular el control de velocidad, se decidió
usar un controlador simple, en este caso, un proporcional.
Fig. 6 -
Diagrama de bloques de control de velocidad con medición de velocidad real.
3.2.2. Control
con Estimador de Velocidad
El control de velocidad
presentado anteriormente depende del valor de velocidad del rotor del motor, lo
que implicaría el uso de un sensor de velocidad. Por las razones anteriormente
descritas, el objetivo de un estimador de velocidad es obtener el valor de
velocidad del rotor de forma indirecta, con los valores medidos de voltaje y
corriente en los bobinados del motor (puesto que es más sencillo y económico
medir voltaje y corriente que velocidad).
Para la
estimación, se propone el estudio de un método basado en un esquema MRAS (Model
Reference Adaptative System, o sistema adaptativo por modelo de
referencia), presentado en [3],[9].
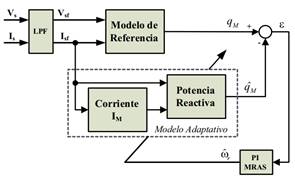
Dicho esquema se
basa en el uso de dos modelos para el cálculo de la potencia reactiva
instantánea en el motor. El primer modelo, llamado modelo adaptativo, depende
de la velocidad del rotor, mientras que el otro, llamado modelo de referencia,
es independiente. El modelo adaptativo se alimenta con la velocidad observada,
que se obtiene de un esquema de adaptación, utilizando un controlador PI, que
obtiene dicha velocidad a partir del error de potencia reactiva calculado entre
ambos modelos. La Fig. 7 muestra un diagrama en bloques del sistema de
estimación de velocidad.
De las ecuaciones
del modelo del motor monofásico, se derivan las siguientes expresiones:
|
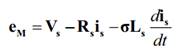
|
(17)
|
|
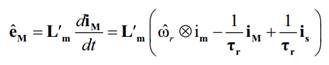
|
(18)
|
En las ecuaciones
(17) y (18), eM y eˆM representan las fuerzas
contra-electromotrices (fcem), calculada y estimada, respectivamente, y
las demás variables son definidas de la siguiente forma:
Fig. 7. Diagrama
de bloques de la estrategia de estimación de velocidad MRAS [9]
Las variables con
acento circunflejo corresponden a los valores observados o estimados.
3.2.2.1. Modelo
de referencia
Si bien se podría
realizar un MRAS utilizando solamente los vectores contraelectromorices, como se
presenta en [9], las resistencias de estator de un motor tienden a variar paramétricamente
con la temperatura, por lo que afectan a la eficiencia del esquema de
estimación.
Con el
conocimiento de las fcem y de las corrientes del estator, puede
definirse la potencia reactiva instantánea que será utilizada en el estimador
de velocidad, con base en la siguiente expresión [9]:
|
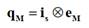
|
(19)
|
El vector qM
puede obtenerse tanto de (17) como de (18). La primera se usa como modelo de referencia,
puesto que no depende de la velocidad del rotor. Asumiendo is ⊗ is = 0, se puede eliminar
el término que
incluye las resistencias de estator, independizándose la estimación de la
variación
paramétrica, y de
esta forma, sustituyéndose (17) en (19), la potencia reactiva resulta:
|
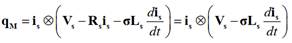
|
(20)
|
Esto, en un
principio, mejoraría la eficiencia de la estimación.
Trabajando la
expresión anterior, se obtiene el siguiente vector qM:
|
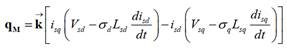
|
(21)
|
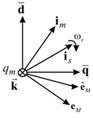
Las corrientes im
e is son vectores giratorios con velocidad ωr.
Fig. 8. Representación
del producto vectorial dado por (20).
Donde el versor k
es perpendicular a los ejes de cuadratura q y d. El error de potencias se
calcula a partir de las magnitudes de los vectores de potencia reactiva, la
obtenida del modelo de referencia y la estimada, como muestra la Fig. 7.
Dado que se
pretende implementar el sistema en un DSC, se procede a realizar la
discretización de la potencia reactiva para el modelo de referencia dada en
(21). La diferenciación se realiza usando una aproximación de diferencia hacia
atrás o backwards. En cualquier muestra k, la potencia reactiva instantánea
del modelo de referencia será:
|
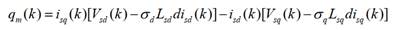
|
(22)
|
Donde:
siendo T el
periodo de muestreo.
3.2.2.2. Modelo
Adaptativo
Para el
observador de velocidad se necesita plantear el modelo adaptativo. Del diagrama
de bloques de la Fig. 7, se puede ver que el primer paso es obtener las
corrientes magnetizantes:
|
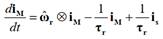
|
(23)
|
Del desarrollo de
la ecuación (23), se obtienen las expresiones de las derivadas de las
corrientes magnetizantes, como se expresa a continuación:
|
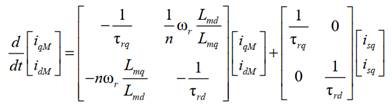
|
(24)
|
La solución de la
ecuación (24), permite obtener los valores de las corrientes magnetizantes.
Dado que la implementación se realizará en un DSC, dicha solución puede
efectuarse mediante la discretización de dicha expresión. En [9] se presenta
dicha discretización utilizando la aproximación de Tustin, sin embargo, para la
implementación de dicha discretización se necesita el valor de referencia de
las corrientes para ambos bobinados del motor. Puesto que el presente trabajo
busca controlar solamente la corriente del bobinado principal, y por lo tanto
no se tiene una referencia para la corriente del
bobinado auxiliar, no es posible utilizar tal método. Trabajando ambos ejes por
separado y utilizando la aproximación de Euler forward, se obtienen las
siguientes expresiones:
|
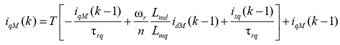
|
(25)
|
|
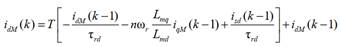
|
(26)
|
Obtenidas las dos
corrientes magnetizantes, se procede al cálculo de la potencia reactiva
instantánea
observada.
|
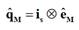
|
(27)
|
La última
expresión, puede representarse matricialmente de la siguiente forma:
|
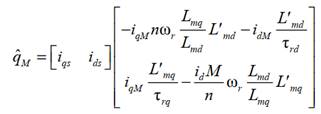
|
(28)
|
Una vez realizado
el cálculo de la potencia reactiva instantánea con ambos modelos, se debe proceder
a calcular el error y alimentar el mismo a un controlador PI que se encargará
de generar la velocidad estimada 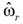
|
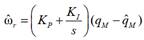
|
(29)
|
De [9] se obtiene
la condición de diseño 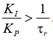
Además, se
menciona que ambos valores deben ser los más altos posibles, sin desestabilizar
el sistema. Sin embargo, utilizándose este criterio, al realizarse la
simulación, el sistema resulta con muy baja estabilidad relativa y se vuelve
fácilmente inestable ante la presencia de perturbaciones. Por otro lado, debido
a la dinámica resultante del estimador, la incorporación del PI hace que
aparezca un cero de fase no mínima que produce un sobrepaso negativo en la respuesta
de velocidad cuando se aplica la referencia, provocando un retraso en la
respuesta y, por ende, un comportamiento no deseado para este tipo de
aplicación.
Debido a esto, se
optó por recurrir a una solución más simple utilizando una acción integral, comprobándose
que el mecanismo de adaptación da muy buenos resultados, ajustándose la
ganancia
KI
para mejorar la velocidad de adaptación. El valor resultante de KI
permite llevar el error de estimación a cero lo más rápido posible, manteniendo
un comportamiento estable en régimen estacionario sin oscilaciones en torno al
valor de referencia.
|
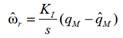
|
(30)
|
La figura Fig. 9
muestra el esquema de la estrategia de control propuesta, con el estimador de velocidad
MRAS:
Fig. 9 -
Sistema de control indirecto de torque y de velocidad con estimador MRAS.
4. Resultados de
Simulación
Para validar el
análisis y propuestas realizadas, se realizaron simulaciones con el software
PSIM, implementando el circuito eléctrico y mecánico del motor como componentes
discretos, mientras que los lazos de control se implementaron usando un bloque
DLL que actúa de forma similar a un controlador digital de señales (DSC),
permitiendo usar código de C++. El paso de simulación utilizado es de 1μs.
4.1. Validación
del modelo del motor.
Como se mencionó
anteriormente, para la validación del modelo del motor, se realiza primero la simulación
energizando únicamente el bobinado principal del motor, dando un pulso de
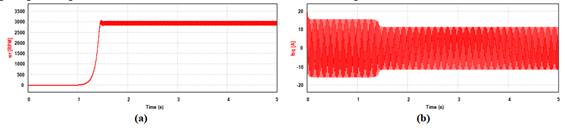
torque al rotor para ayudar al arranque. La Fig. 10 (a) presenta la velocidad
del rotor y la Fig. 10 (b), la corriente del estator, en la cual se observa la
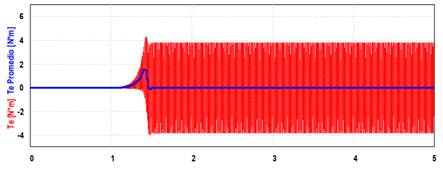
corriente que toma el motor en el arranque. La Fig. 11 presenta el torque
eléctrico sin carga en el eje del mismo. Se agregó el torque promedio (curva en
color azul) para poder apreciar la evolución durante el transitorio de
arranque.
Fig. 10. Respuesta al simular el motor a lazo abierto. (a)
Velocidad. (b) Corriente del estator.
Fig. 11. Torque eléctrico del motor a lazo abierto.
Cabe destacar que
el torque eléctrico presenta un incremento solamente durante el arranque, mientras
que, en régimen permanente, sin carga en el eje, presenta una componente
oscilatoria con promedio nulo, propia de los motores monofásicos, causada por
la asimetría de los bobinados.
En base a los
resultados obtenidos, se puede apreciar que la opción de utilizar un inversor monofásico
para el accionamiento del motor monofásico de la bomba, en vez de uno
trifásico, ofrece los resultados esperados, lo que nos indica que el control
indirecto de torque y el control de velocidad, deben ofrecer también buenos
resultados. Los mismos se describen a continuación.
4.2. Control de
corriente
Una vez validado
el modelo del motor, se procede a simular el control de corriente. Esta
simulación se realiza conectando el bobinado auxiliar a la alimentación por
medio de un capacitor permanente de 5 μF, de modo que el motor arranque
sin necesidad de un torque externo.
Como se pretende
implementar físicamente el sistema de control en un DSC, se procede a realizar el
rediseño digital de la expresión del controlador I propuesto, dada por (14).
Para ello, se usa la aproximación de Tustin. Realizándose la sustitución y
aplicándose la transformada Z inversa, se obtiene entonces la siguiente
ecuación recursiva a diferencias finitas, la cual se utiliza en el algoritmo de
control digital emulado por la DLL en PSIM.
|
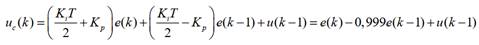
|
(31)
|
con Ki = 19,6712, Kp = 1, fs = 10
kHz, T = 1/ fs = 0,1 ms.
De la misma
forma, se aplica el rediseño digital a la expresión del controlador resonante
dada en (15), utilizándose la aproximación invariante al escalón o ZOH,
resultando en la siguiente expresión:
|
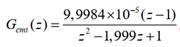
|
(32)
|
y, aplicándose la
transformada Z inversa, se obtiene la ecuación recursiva a diferencias finitas
que se utiliza en el algoritmo de control digital emulado por la DLL en PSIM.
|
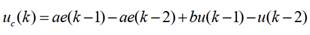
|
(33)
|
con a = 9,9984 x
10-5 y b = 1,999 considerando la ganancia del resonante ki
= 1. A la ecuación (33) se le suma la acción proporcional de valor igual a 0,15
para asentar rápidamente la respuesta de corriente y reducir las oscilaciones
iniciales que impone el controlador resonante.
En lazo abierto,
la corriente del estator en régimen permanente presenta un valor de pico de aproximadamente
10 A. Dado que llegando a dicho valor es posible que se pierda control sobre la
planta debido a la saturación del actuador, se elige un valor de corriente para
la referencia de 7 A de pico a 50 Hz. Como carga, se aplica un torque de 0,05
Nm al rotor en t = 7,005 s (a modo de que actúe en el momento en el que la
corriente está en su valor máximo; el peor caso).
Resultados usando
controlador PI:
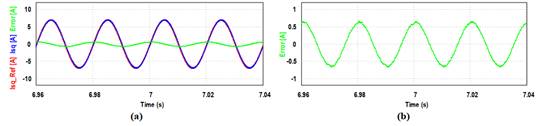
En la Fig. 12
(a), se aprecian las señales de referencia del lazo de corriente y la corriente
controlada del bobinado principal, juntamente con la señal de error, y, en la
Fig. 12 (b) se observa una ampliación de la señal de error de corriente, cuya
amplitud es del 8,6 % del valor de pico de la corriente isq. Se puede
concluir, que a pesar de que el error no es nulo, debido al desfasaje que
provoca la acción integral en el rango de frecuencia de interés, la amplitud de
la corriente controlada es igual a la amplitud de la referencia que está siendo
impuesta, por lo que se considera el diseño del controlador como aceptable para
esta aplicación. Se puede destacar como la corriente sigue de cerca a la referencia,
aun teniendo en cuenta la perturbación de torque aplicada, y el hecho de que,
como se mencionó al momento de diseñar el controlador, la corriente del bobinado
auxiliar se acopla magnéticamente al primario, actuando también como
perturbación.
Por otro lado, en
la Fig. 13 (a), se presenta la respuesta de velocidad del eje del motor, la
cual, luego de alcanzar el valor nominal sin torque en el eje, se mantiene muy
próximo al valor de referencia, decayendo luego a los 7,005 segundos de
aplicado el torque en el eje. Es importante destacar, que la velocidad que se
observa es la que se tiene únicamente con el control de corriente, Fig. 4, con
lo cual se aprecia en base al valor de velocidad, el buen desempeño en régimen
estacionario antes de la aplicación de la perturbación.
Fig. 12. Respuesta de corriente a lazo cerrado con
controlador PI. (a) Referencia, Corriente de estator y Error de corriente. (b)
Acercamiento de la señal de error de corriente.
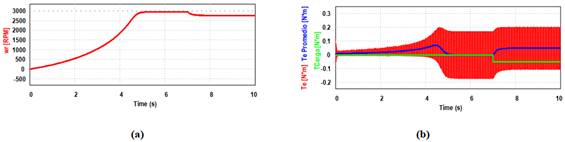
Fig. 13.
Respuesta de velocidad y torque a lazo cerrado de corriente con controlador PI.
(a) Velocidad.
(b).
Torque eléctrico instantáneo (en rojo) y promedio (en azul) y torque de carga
(en verde).
En la Fig. 13
(b), se observa la componente oscilante en el torque, cuyo valor promedio
evoluciona con un transitorio en el arranque para superar la inercia, y luego
permanece nulo hasta la aplicación de la perturbación, momento en el cual el
torque eléctrico tiene que aumentar para contrarrestarla.
Resultados usando
controlador por el Principio del Modelo Interno: Controlador Resonante:
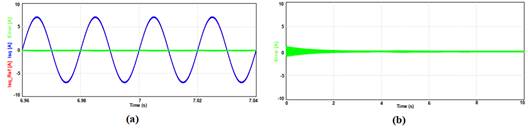
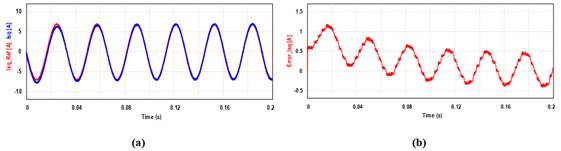
En la Fig. 14 (a)
se aprecian las señales de referencia del lazo de corriente y la corriente
controlada del bobinado principal, juntamente con la señal de error, y,
en la Fig. 14 (b), la señal de error desde el arranque del motor. Se puede
apreciar que el controlador resonante, lleva prácticamente a cero el error
de corriente una vez superado el arranque del motor, a un valor no mayor a los
0,1 A de pico lo que representa un 1,4 % del valor de pico de la
corriente nominal. Se considera que el error es ruido básicamente de la
conmutación PWM. Según la Fig. 14 (b), el tiempo de convergencia del error a cero,
puede reducirse incrementándose la ganancia ki, observándose siempre
que la estabilidad relativa no reduzca significativamente sus márgenes. No
obstante, debe tenerse en cuenta que, durante el transitorio de arranque, la
frecuencia de la referencia de corriente es variable, por lo que la actuación
del controlador resonante no produce la cancelación correcta del efecto de la
referencia.
Fig. 14. Respuesta de la corriente con controlador
Resonante. (a) Referencia y corriente de estator durante perturbación. (b)
Error de corriente en arranque y régimen permanente antes y después de la
perturbación
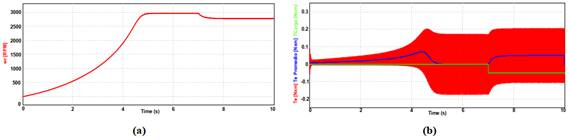
Fig. 15.
Respuesta de velocidad y torque a lazo cerrado de corriente con controlador
Resonante. (a) Velocidad.
(b).
Torque eléctrico instantáneo (en rojo) y promedio (en azul) y torque de carga
(en verde).
Finalmente, se
aprecia que, durante el transitorio de aplicación de la perturbación de torque
a los 7,005 segundos, el controlador resonante responde con un excelente
rechazo de perturbación sin afectar prácticamente el error de corriente y la
respuesta del torque electro eléctrico es similar a la obtenida con el
controlador PI.
4.3. Control de
velocidad con controlador proporcional
Luego de validar
el control de corriente, se procede a simular el efecto de cerrar el lazo de velocidad,
usando la velocidad medida del motor con el objetivo de poder comparar el
desempeño, al utilizar el estimador de velocidad.
Como referencia
de velocidad, se usa una rampa de 500 RPM a 2500 RPM. A su vez, el lazo interno
de control de corriente, el cual utiliza en esta primera etapa un PI, tiene
como referencia un pico de corriente de 7 A. Por último, se aplica una
perturbación de torque al eje del motor en el instante t = 10 segundos.
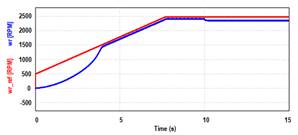
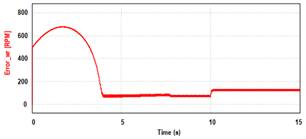
Se observa en la
Fig. 16 (a) la respuesta de la velocidad ωr. del eje del motor,
la cual se ajusta a la rampa luego de algunos segundos con un pequeño error,
aumentando el mismo su valor, una vez aplicada la perturbación de torque a los
10 segundos. Este error se debe a que el controlador no presenta un polo en z =
1 que posibilite llevarlo a cero. La Fig. 16 (b), describe la evolución de la señal
de error a lo largo del periodo de simulación.
|
|
|
|
(a)
|
(b)
|
Fig. 16.
Respuesta del lazo de control de velocidad. (a) Seguimiento de referencia. (b)
Error de velocidad.
Puesto que en
régimen permanente el error de velocidad se mantiene por debajo de 200 RPM para
una referencia de 2500 RPM, es decir, un 8% de error, se considera aceptable la
utilización de un controlador proporcional, sin la necesidad de agregar una
acción integral; considerándose que el lazo de control de corriente, atiende
las necesidades para imponer el torque necesario en la carga.
4.4. Estimación
de velocidad
Los siguientes
resultados de simulación corresponden a la validación del estimador de
velocidad, a través de una comparación entre la velocidad medida y la estimada,
usando el mismo perfil de referencia y perturbación del inciso anterior.
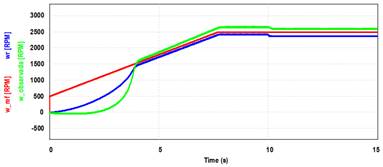
Fig. 17.
Velocidad observada y velocidad medida del motor versus perfil de referencia.
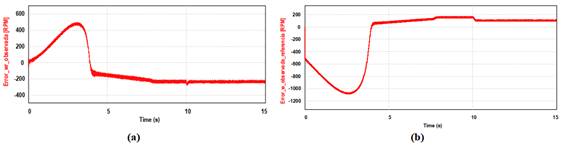
Fig. 18.
Errores de la velocidad. (a) Error de la velocidad observada respecto a la
real. (b) Error de la velocidad observada respecto a la referencia.
El cálculo de la
velocidad observada depende de las derivadas de las corrientes medidas del bobinado
principal y auxiliar, por lo que se puede esperar un desempeño pobre en la
etapa transitoria de la respuesta del motor, lo que se ve traducido en un valor
de error alto y un retardo en la respuesta luego de aplicado el valor inicial
de 500 RPM en t = 0, como se muestra en la Fig. 17.
Luego de dicha
etapa transitoria, el error disminuye notablemente, manteniéndose próximo de
los 2500 RPM, con una pequeña disminución en el momento en que se aplica la
perturbación de torque al rotor. Como se mencionó anteriormente, este error
puede reducirse utilizando una acción integral en el lazo de velocidad.
Finalmente, para
apreciar cómo se comporta el lazo de control de corriente con el lazo de velocidad,
utilizándose la velocidad estimada, en la Fig. 19 se muestra el seguimiento de
referencia de la corriente del bobinado primario, junto con el error, en la
rampa inicial de velocidad, y la Fig. 20 al momento de la perturbación, cuando
el motor ya se encuentra en velocidad de régimen. Se puede apreciar como la
corriente sigue de cerca su referencia, durante el arranque y aun luego de
aplicar una perturbación al eje a los 10 s. En este caso, el controlador de
corriente utilizado es el PI.
En la Fig. 19
puede observarse un transitorio en el seguimiento de la referencia de la rampa
de arranque, lo que se traduce en un error inicial elevado, que se va
reduciendo rápidamente hasta llegar a un valor de 0,5 A de pico, que es valor
final con el diseño realizado.
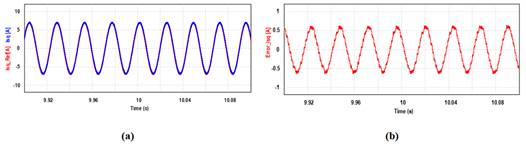
Comparando la
figura anterior con la Fig. 20, se puede ver como la frecuencia eléctrica
aumenta, lo que es de esperarse puesto que es dicha frecuencia la que se
manipula para variar la velocidad del eje del motor. Además, se puede apreciar
un ligero aumento en el valor máximo del error. No obstante, la corriente sigue
muy bien a la referencia, con buen rechazo de perturbación.
Fig. 19 -
Corriente del bobinado primario durante el arranque. Control con PI.
(a) Seguimiento
de referencia. (b) Error.
Fig. 20 -
Corriente del bobinado primario durante una perturbación de torque. Control con
PI.
(a)
Seguimiento de referencia. (b) Error.
5. Conclusiones
Del estudio de
diferentes estrategias de control se puede concluir que, si bien existen
métodos que permiten un control directo sobre variables de funcionamiento de un
motor monofásico, como velocidad y torque, estos suelen necesitar actuadores
más complejos para un control preciso.
Sacrificándose
ciertos grados de libertad sobre esas variables, es posible llegar a un control
indirecto del torque, como el planteado en este trabajo, simplificándose el
actuador y obteniéndose a la vez, muy buenas prestaciones para la presente
aplicación de bombeo de agua en bajas potencias.
El lazo de
corriente implementado funciona correctamente tanto con el controlador PI, como
con un controlador por modelo interno. A pesar de que existe un pequeño valor
de error menor al 10%, el controlador PI no presenta inconvenientes en el
transitorio de arranque dado que no depende de la frecuencia de la velocidad.
Sin embargo, el controlador resonante, una vez superado el transitorio, es el
que presenta mejor desempeño en régimen permanente. Ambos controladores,
presentan un muy buen desempeño para rechazo de perturbaciones, y considerando
que en cuanto complejidad de implementación son similares, es preferible
siempre la utilización del controlador resonante, ya que el mismo garantiza
seguimiento robusto de la referencia.
En cuanto al
control de velocidad, planteado por medio de la frecuencia eléctrica, demostró
dar buenos resultados en simulación, siguiendo sin problemas la referencia y
manteniendo un valor de error bajo frente a perturbaciones.
El algoritmo de
estimación de velocidad MRAS presenta cierta complejidad en su implementación en
código, y su desempeño se ve afectado en régimen transitorio. Aun así, sigue de
cerca el valor de velocidad real en régimen permanente, por lo que es posible
su uso como alternativa a un sensor de velocidad, con la consecuente reducción
de costos y de mantenimiento, tomándose siempre los recaudos en el régimen
transitorio en caso de que sea necesario.
6.
Agradecimientos
Este trabajo ha
sido llevado a cabo gracias al apoyo del CIN y al financiamiento de la FI-UNaM con
el Proyecto de Desarrollo Tecnológico y Social, Código 16/I1083-PDTS.
7. Referencias
[1] Packiam Periasamy, N.K. Jain, I.P. Singh, “A review on
development of photovoltaic water pumping system,” in Renewable and Sustainable
Energy Reviews, Volume 43, 2015, Pages 918-925, ISSN 1364-0321, https://doi.org/10.1016/j.rser.2014.11.019.
[2] S. S. Chandel, M. Nagaraju Naik, y R. Chandel, «Review of
solar photovoltaic water pumping system technology for irrigation and community
drinking water supplies», Renew. Sustain. Energy Rev., vol. 49, pp. 1084-1099,
sep. 2015.
[3] M. A. Vitorino, M. B. de Rossiter Correa, C. B. Jacobina and
A. M. N. Lima, "An Effective Induction Motor Control for Photovoltaic
Pumping," in IEEE Transactions on Industrial Electronics, vol. 58, no. 4,
pp. 1162- 1170, April 2011, doi: 10.1109/TIE.2010.2054053.
[4] B. Reshef, H. Suehrcke, y J. Appelbaum, «Analysis of a
photovoltaic water pumping system», Electrical and Electronics Engineers in
Israel, 1995., Eighteenth Convention of. pp. 1.5.3/1-1.5.3/5, 1995.
[5] M. A. Elgendy, B. Zahawi, y D. J. Atkinson, «Analysis of the
performance of DC photovoltaic pumping systems with maximum power point
tracking», Power Electronics, Machines and Drives, 2008. PEMD 2008. 4th IET
Conference on. pp. 426-430, 2008.
[6] S. Abdourraziq y R. El Bachtiri, «A perturb and observe method
using fuzzy logic control for PV pumping system», Multimedia Computing and
Systems (ICMCS), 2014 International Conference on. pp. 1608-1612, 2014.
[7] S.R. Wenham, M.A. Green, M.E. Watt, R. Corkish, «Applied
Photovoltaics». Earthscan, Second Edition, 2007.
[8] N. K. Lujara, J. D. Van Wyk, y P. N. Materu, «Loss models of
photovoltaic water pumping systems», Africon, 1999 IEEE, vol. 2. pp. 965-970
vol.2, 1999.
[9] R. P. Vieira.
“Servocontrole de velocidade aplicado a motores de indução monofásicos sem sensores
mecánicos”. Santa Maria: Universidade Federal de Santa Maria Centro de
Tecnologia, Programa de PósGraduação em Engenharia Elétrica, 2008.
[10] A. S. Ba-thunya, R. Khopkar, Kexin Wei and H. A. Toliyat,
"Single phase induction motor drives-a literature survey," IEMDC
2001. IEEE International Electric Machines and Drives Conference (Cat.
No.01EX485), Cambridge, MA, USA, 2001, pp. 911-916, doi:
10.1109/IEMDC.2001.939428.
[11] M. B. de Rossiter Correa, C. B. Jacobina, A. M. N. Lima and
E. R. C. da Silva, "Rotor-flux-oriented control of a single-phase induction
motor drive," in IEEE Transactions on Industrial Electronics, vol. 47, no.
4, pp. 832-841, Aug. 2000, doi: 10.1109/41.857963.
[12] F. A. S. Neves, E. B. S. Filho, J. M. S. Cruz, R. P. Landim,
Z. D. Lins and A. G. H. Accioly, "Single-phase induction motor drives with
direct torque control," IEEE 2002 28th Annual Conference of the Industrial
Electronics Society. IECON 02, Seville, Spain, 2002, pp. 241-246 vol.1, doi:10.1109/IECON.2002.1187514.