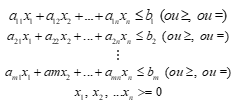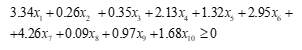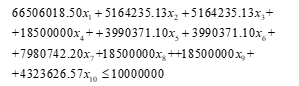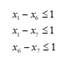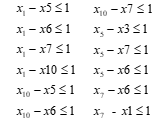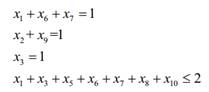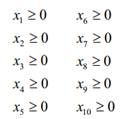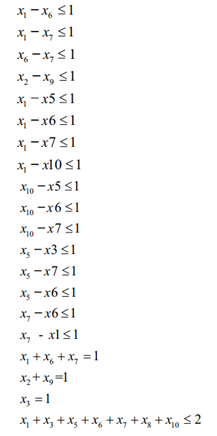Instructions for the preparation camera ready paper

1. Introdução

Atualmente o Sistema Elétrico de Potência – SEP tem a função especifica de gerar, transportar e distribuir energia elétrica a todos os usuários. Esta energia deve possuir qualidade adequada e disponibilidade a qualquer momento em que for solicitada.

O consumo de energia teve um crescimento considerável nos últimos anos, fazendo com que aumentasse a preocupação com a quantidade de energia disponibilizada e principalmente sua qualidade. Esse crescimento fez com que muitos estudos e pesquisas ocorressem em torno do assunto para que pudesse atender o crescimento acelerado das cargas.

A confiabilidade do Sistema Elétrico de Potência se torna a base para a realização do planejamento da expansão de redes de média tensão, em Ferreira [6] afirma que é essencial identificar os pontos que mais necessita de manutenção, reforma ou expansão. Essa necessidade pode ser identificada pelos valores encontrados em indicadores coletivos e individual e ou por equipamentos que mais ocasionam falhas, entre outros meios. O aumento de carga no SEP sem um planejamento pode ocasionar violações em indicadores.

De acordo com [1], tanto sobre o ponto de vista da operação, quanto do planejamento de curto, médio, e longo prazo, o comportamento do sistema elétrico deve ser acompanhado sistematicamente. Assim, para manter um histórico permanente atualizado, analisar o comportamento frente a contingencia e alterações, diagnosticar e prever efeitos de medidas a serem adotadas, planejar ampliações e alterações de configuração, o sistema elétrico deve ser criteriosamente, representado por meio de uma modelagem adequada ao tipo de estudo a ser realizado.

Além a preocupação com a modelagem do SEP, [2] apresenta questões importantes a serem consideradas quando se considera o SEP e fluxo de potência:

a) Qual a maneira mais econômica de dividir a carga entre os vários geradores de uma rede elétrica em função de seus custos de geração? Como minimizar as perdas de transmissão através da escolha de melhores rotas? Quais as melhores configurações de rede para atender as demandas das cargas?

b) Qual e o efeito de interligações, em novas linhas, novas cargas e novos geradores?

c) Como manter o estado de funcionamento em regime permanente?

As questões do item (a) estão relacionadas ao estudo de despacho econômico de energia. A letra (b) diz respeito ao planejamento e expansão do sistema. A questão (c) é concernente aos problemas de controle e operação do sistema. Todos esses estudos são de fundamental importância para que se possa manter a continuidade do sistema elétrico de potência em regime permanente atendendo de forma continua as cargas instalada no SEP.

Além das ferramentas computacionais para modelagem e simulação do SEP, é muito empregado a otimização matemática para o planejamento da expansão e ações no SEP. Segundo [3], os principais objetivos da otimização do planejamento da expansão da transmissão em ambientes competitivos são: aliviar o congestionamento de linhas de transmissão e transformadores, reduzir o custo de investimento, melhorar a confiabilidade do sistema, incentivar a concorrência entre os participantes do Mercado; e aumentar a flexibilidade da operação do sistema.

O presente estudo tem como objetivo analisar o sistema elétrico para fins de melhoria dos indicadores de qualidade, diminuir os custos de manutenção, provocar o aumento do faturamento, e consequentemente melhorar a imagem da empresa que está fornecendo energia. Para obter os resultados desejados serão utilizados os softwares ANAREDE e o OTIMIZA. O ANAREDE será empregado na modelagem do SEP e estudo do fluxo de potência, enquanto o OTIMIZA será empregado para auxiliar na tomada de decisão de quais ações serão executadas, considerando a maximização do Valor Presente Líquido – VPL de cada obra.

2. Descrição do problema

O planejamento da expansão do SEP apresenta-se como um problema de grande complexidade e muitas peculiaridades. Segundo [4], a principal dificuldade na otimização da adequação do SEP é que a mesma medida destinada a fornecer a adequação de um componente do sistema ou o SEP inteiro, produz efeitos diferentes do sistema em diferentes nós. O efeito depende do local no sistema onde a ação é tomada, o tempo da desta ação, e acima de tudo, as características técnicas e econômicas do sistema em que a ação é implementada. Já [5] destaca alguns fatores desta complexidade:

a) Deve-se considerar uma visão de longo prazo para que os empreendedores possam se beneficiar da economia de escala. Assim como o tempo necessário para construção de alguns empreendimentos faz com que seja necessário decidir sobre sua construção muito antes da sua real necessidade.

b) Os empreendimentos de geração e transmissão apresentam dependências temporais e espaciais e necessitam ser analisados de forma conjunta no espaço e no tempo.

b) Precisam ser avaliadas, simultaneamente, as características técnicas, econômicas e ambientais dos empreendimentos.

c) Existem incertezas aos valores previstos para o comportamento do consumo, dos recursos hidricos e do custo e disponibilidade de outras fontes primárias de energia.

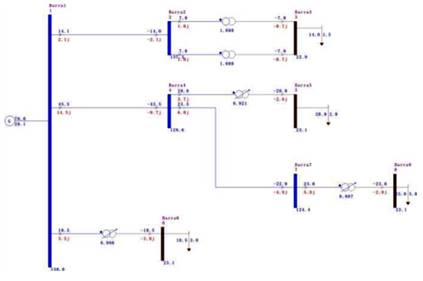
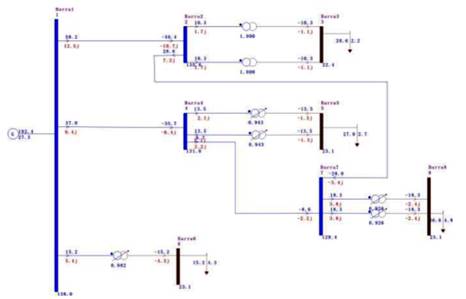
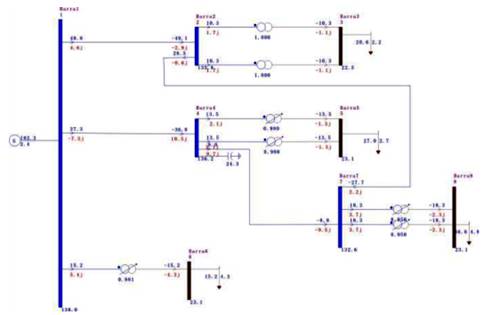
Para o presente estudo, foi utilizado um sistema didático composto por 8 barras (07 PQ e 01 PV), 05transformadores, 04 cargas e apenas um gerador. A Fig. 1 representa graficamente este sistema.

Fig. 1. Sistema didático 8 barras.

Para o planejamento da expansão do referido sistema, considerou-se um período de expansão da carga de 10 anos, como apresentado na Tabela 1.

Tabela 1. Projeção de Carga

Barra	Projeção para 10 anos
Barra	MW	Mvar
03	20,64	2,21
05	27,01	2,70
06	15,24	4,30
08	36,63	4,78

Ao adicionarmos ao sistema a projeção da carga, este entra em colapso, apresentando os seguintes problemas:

a) Problema 01: Sobrecarga da linha entre as barras 01 e 04.

b) Problema 02: Sobrecarga no transformador entre as barras 04 e 05.

c) Problema 03: Sobrecarga no transformador entre as barras 07 e 08.

d) Problema 04: Baixo nível de tensão na barra 08.

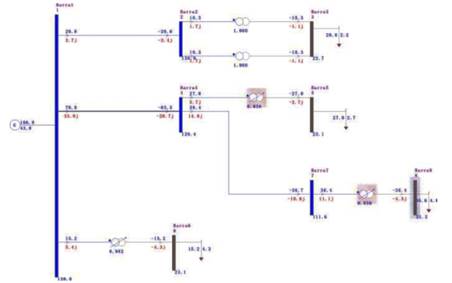
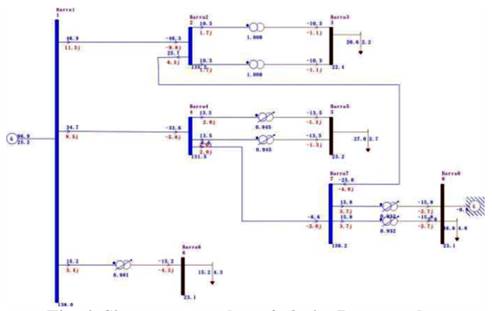
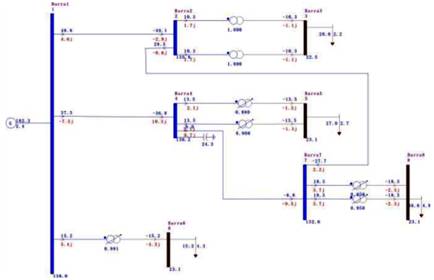
Além dos problemas relatados o sistema apresentou um percentual de perdas de aproximadamente 7,17 %. A Fig. 2 apresenta o sistema com indicação dos referidos problemas.

Fig. 2. Sistema didático em colapso.

Tabela 2. Relação de obras para sistema 8 barras

Descrição	Investimento [R$]	VPL [R$]
Obra 01: Inclusão de linha entre as barras 01 e 04	66.506.018,50	-45.384.442
Obra 02: Inclusão de transformador 25MVA entre as barras 4 e 5	5.164.235,13	-3.520.041
Obra 03: Inclusão de transformador 25MVA entre as barras 7 e 8	5.164.235,13	7.377.574
Obra 04: Inclusão de GD (5MW) na barra 8	18.500.000,00	-5.030.252
Obra 05: Inclusão de linha entre as barras 4 e 7	3.990.371,1	-2.797.878
Obra 06: Inclusão de linha entre as barras 2 e 4	3.990.371,1	14.664.914
Obra 07: Inclusão de linha entre as barras 2 e 7	7.980.742,2	18.958.754
Obra 08: Inclusão de GD (5MW) na barra 3	18.500.000,00	-17.930.856
Obra 09: Inclusão de GD (5MW) na barra 5	18.500.000,00	-12.365.889
Obra 10: Inclusão de banco de capacitor na barra 4	4.323.626,57	6.300.400

Tabela 3. Benefícios proporcionados por cada obra

Obras	Benefício ao sistema	Redução das perdas
1	Corrige o problema de sobrecarga na linha entre as barras 01-04	3,34
2	Corrige o problema de sobrecarga no Trafo entre as barras 04 - 05	0,26
3	Corrige o problema de sobrecarga no Trafo entre as barras 07 – 08 e barra 08	0,35
4	Corrige o problema nas barras 07 - 08	2,13
5	Corrige o problema na barra 08.	1,32
6	Corrige o problema de sobrecarga na linha entre as barras 01-04	2,95
7	Corrige os problemas de sobrecarga nas linhas e barras, permanecendo os problemas nos transformadores entre as barras 04 - 05, e 07 e 08.	18.958.754
8	Proporciona redução de perdas do sistema	-17.930.856
9	Resolveu o problema no transformador entre as barras 04 e 05	-12.365.889
10	Corrige o problema na barra 08	6.300.400

A partir das obras relacionadas acima, deve se tomar a decisão de quais obras devem ser executadas, considerando as que proporcionem o maior VPL e maior redução das perdas.

Otimização Matemática

Os métodos de otimização baseiam-se na utilização de técnicas de programação matemática, que tem por escopo a otimização de algumas funções objetivo, sujeitas a um conjunto de restrições. O método da Programação linear, aqui inserido, possui variáveis inteira (discreta), neste caso, a programação contem variáveis que são reais e continuas [1].

A formulação do problema a ser resolvido por programação linear segue alguns passos básicos. Deve ser definido o objetivo básico do problema, ou seja, a otimização a ser alcançada. Por exemplo, maximização ou a minimização de custos. Tal objetivo será representado por uma função. Para que esta função objetivo seja matematicamente especificada, devem ser definidas as variáveis de decisão envolvidas.

O problema geral de programação linear pode ser definido por Maximizar ou Minimizar uma função.

Função objeto:

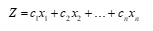
(1)

Restrições a quais a função objeto está sujeita:

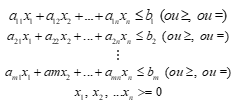
(2)

Onde:

a = atribuições em função dos objetivos estipulados (obras)

b = obras mínimas combinatórias para a restrição atribuída

c = esta variável representa a obra para melhoria do SEP

x = representa o valor atribuído a obra

Para o estudo em questão foi utilizado o software OTIMIZA. O programa inserido no “Otimiza” contém uma função objeto, contendo 10 variáveis (x1...10), as quais representam obras a serem executadas para correção dos problemas apresentados após o colapso do sistema, conforme Tabela.

O problema de programação Linear é formado por uma função objetivo (1) e um conjunto de restrições (2) que são funções das variáveis de decisão do problema. O programa seleciona aquelas obras que propiciam o maior benefício, sendo atendidas restrições impostas e inter-relacionamento das obras. As restrições estão definidas através das obras Excludentes e Interdependentes.

A partir do levantamento dos benefícios e custos proporcionados por cada obra, adotamos 04 passos para a formulação da programação matemática:

Passo 01: Escolha da variável de decisão.

x_i= obras destinadas a solucionar o colapso do sistema.

i=1...10.

Passo 02: Elaboração da função objetivo.

A partir do momento que conhecemos as variáveis de decisão, podemos expressar a função objetivo em função destas variáveis. Devido nosso objetivo ser maximizar os benefícios proporcionados por estas obras, levamos em consideração o VPL proporcionado por cada obra.

(3)

Passo 03: Formulação das restrições.

Restrição de redução das perdas

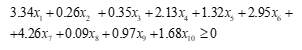
(4)

Ao criarmos esta restrição, forçamos o programa a localizar uma resposta ótima que proporcione ao sistema um redução das perdas maior ou igual a zero.

Restrição de limite de investimento

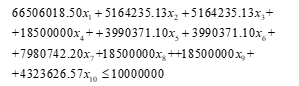
(5)

Não raras vezes, o capital disponível para execução de obras de reparos é limitado, desta forma, deve-se criar uma restrição para a disponibilidade de recurso financeiro.

c) Restrições de obras excludentes

Obras que solucionam o problema 01 (LT br 01-04)

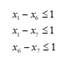
(6)

Obras que solucionam o problema 02 (TRAFO br 04-05)

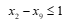
(7)

Obras que solucionam o problema 04 (br 08).

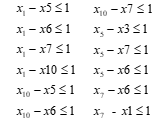
(8)

d) Restrições de obras concomitantes

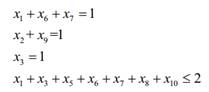
(9)

Deve-se destacar que a obra 03 (x3) será realizada em qualquer hipótese, pois é a única que apresenta como benefício a solução do problema 03. Devido a obra 8 (x8) não apresentar benefícios de melhora a quaisquer problemas enfrentados pelo sistema, esta não foi adicionada as restrições.

A última restrição permite a execução de até duas obras concomitantes. Esta flexibilização é necessária devido a obra 03 ser executada em todas as condições.

Passo 04: Restrições de não negatividade.

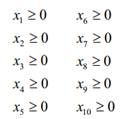
(10)

A partir de (1) e (2), pode-se elaborar ao problema completo (11) utilizando as equações apresentadas acima:

(11)

Sujeito a:

3. Descrição Simulações e Obras

De posse do programa matemático (11), composto por função objetiva e suas restrições, utilizou-se a versão didática do Software Otimiza, para a obtenção da solução ótima. Esta solução deve representar quais obras deveriam ser executadas para obtenção do maior VPL. Durante as simulações, considerou-se alterações nos valores das restrições, como: redução de perdas, limite de capital de investimento e flexibilização de obras concomitantes.

As Tabelas 4 e 5 apresentam o resumo das simulações realizadas. Destaca-se que para a restrição dos valores de redução de perdas superiores a 8% o software retornou solução inviável.

A partir da flexibilização das restrições pode-se obter 04 diferentes soluções ótimas, apresentadas na Tabela 5, as quais apresentam diferentes investimentos, valor presente líquido e redução de perdas proporcionadas.

Tabela 4. Resumo das Simulações - Restrições

Redução das perdas >=	Investimento (R$) <=	Obras concomitantes <=
4	20.000.000	2
6	40.000.000	2
6	30.000.000	3
4	20.000.000	3

Tabela 5. Resumo das Simulações - Resultados

Redução das perdas >=	Obras	Investimento (R$) <=	VPL
4	2, 3 e 7	18.309.212	22.816.287
6	2, 3, 4 e 7	36.809.212	17.786.035
6	2, 3, 7 e 10	22.632.839	29.116.687
4	2, 3, 6 e 10	18.642.468	24.822.847

4. Conclusões

Ao analisarmos as Tabelas 4 e 5, pode-se tomar como a solução ótima a execução das obras 2, 3, 7 e 10, no entanto, como citado anteriormente, a principal dificuldade na otimização é que a mesma medida destinada a fornecer a adequação de um componente do sistema ou o SEP inteiro, produz efeitos diferentes no sistema em diferentes nós, desta forma, interferindo na perda global do sistema. Assim, optou-se em implementar as soluções no software ANAREDE para obter as reduções das perdas reais proporcionadas pelas obras. A Fig. 3, Fig. 4, Fig. 5 e Fig. 6, apresentam o sistema com as obras executadas.

Fig. 3. Sistemas com obras 2, 3 e 7 executadas.

Fig. 4. Sistemas com obras 2, 3, 4 e 7 executadas.

Fig. 5. Sistemas com obras 2, 3, 7 e 10 executadas.

Fig. 6. Sistemas com obras 2, 3, 6 e 10 executadas.

A Tabela 6 apresenta a reduções das perdas globais do sistema, proporcionadas por cada obra executada no sistema.

Tabela 6. Resumo das Simulações - Restrições

Obras	Investimento (R$)	VPL (R$)	Redução de perdas
2, 3 e 7	18.309.212	22.816.287	2,82
2, 3, 4 e 7	36.809.212	17.786.035	2,72
2, 3, 7 e 10	22.632.839	29.116.687	2,72
2, 3, 6 e 10	18.642.468	24.822.847	3,85

Ao considerarmos as reduções de perdas globais proporcionadas por cada conjunto de obras, chega-se a conclusão de que a resposta ótima ao sistema passa a ser a execução das obras 2, 3, 6 e 10. Pois apesar deste conjunto de obras não apresentar o maior VPL, ele proporciona a maior redução das perdas e um custo de investimento 18% menor em relação ao conjunto que possui o maior VPL.

Agradecimentos

Agradecemos ao Programa de Pós-Graduação Engenharia Elétrica - PPPGE da Universidade Federal de Santa Maria - UFSM pela oportunidade de estar realizando a disciplina Otimização Aplicada a Sistema Elétrico, em especial ao Professor Dr. Daniel Pinheiro Bernardon pelos conhecimentos passados. Cabe agradecimentos aos colegas da Faculdade de Engenharia da Universidade de Missiones por suas contribuições a este artigo.

Referências

[1]	Elgerd, O. I. (1981). Fluxo do Fluxo de pôtencia , Capitulo 4. McGraw-Hill, São Paulo.
[2]	Gardeshi, M.E., Rahimi-kian, A. (2011). Invasive Weed Optimization Feature in Market- BasedTransmission Expansion Planning. 16th International Conference on Intelligent System Applications to Power Systems, páginas 1-4.
[3]	Haffner, S.L. (2000). O planejamento da expansão dos sistemas elétricos no contexto de um ambiente competitivo, page or chapter numbers if relevant. Universidade Estadual de Campinas, Faculdade de Engenharia e de Computação, Campinas-SP.
[4]	Kagan, N., Oliveira, C.C.B., e Robba, E.J. (2004). Introdução aos Sistemas de Distribuição de Energia Elétrica. Edgar Blucher, São Paulo.
[5]	Krupenev, D.S. and Perzhabinsky, S.M. (2013). Adequacy optimization in long-term expansion planning of electric power systems. 4th International Youth Conference on Energy (IYCE), páginas 1-4.
[6]	Ferreira, M. I. J. (2019). Planejamento da Manutenção de Sistemas de Distribuição Baseado em índices de Confiabilidade. Pontifíca Universidade Catolica do Rio de Janeiro, Dissertação. Rio de Janeiro – RJ.