La Universidad Centra “Marta Abreu” de Las Villas (UCLV), a través de su Facultad de Enseñanza Dirigida (FED)

Vol. 3 N° 1, enero-junio 2021, pag. 77-86

ISSN 2618-5520 on line

DOI - https://doi.org/10.36995/j.masingenio.2021.03.01.007

Diseños de Experimentos en la Búsqueda de las Condiciones Óptimas para la Transferencia de Tecnologías

González Suárez E^.a, https://orcid.org/0000-0001-5741-8959, (erenio@uclv.edu.cu)

Curbelo Sánchez A.^a , https://orcid.org/0000-0002-9955-0437, (acurbelo@uclv.edu.cu)

de León Benítez J.B.^a, https://orcid.org/0000-0002-1689-2301, (juanba@uclv.edu.cu)

Miño Valdés Juan E.^b, https://orcid.org/0000-0003-1033-3506, (minio@fio.unam.edu.ar)

^aUniversidad Central de las Villas (UCLV), Departamento. Ing.Química, Santa Clara, Villa Clara, Cuba

^b Universidad Nacional de Misiones (UNaM), Facultad de Ingeniería (FI), Oberá, Misiones, Argentina

Resumen

El objetivo de este trabajo fue precisar las posibilidades y necesidades de la formación de Ingenieros Químicos en la Universidad, con dominio de herramientas para investigación científica, con vistas a encontrar las condiciones óptimas para la transferencia de tecnología. En el análisis se parte de las tradicionalmente utilizadas analogías entre las transferencias de impulso, de calor de masa, sus grupos adimensionales y diseño de experimentos. Se incluye la modelación matemática para obtener información sobre los fenómenos de transporte reales y las posibilidades de escalados de instalaciones de la industria química. Se refuerza la necesidad de un adecuado respaldo experimental para la propuesta de toma de decisiones y como a través de los modernos métodos cibernéticos se pueden alcanzar más rápidamente respuestas a las demandas de la industria. Se enfatiza el significado, como instrumento de trabajo, que tienen la incorporación de estos métodos en la formación científica de los ingenieros químicos.

Palabras claves - Diseño de experimentos, Condiciones óptimas, Transferencia de tecnologías

Abstract

The objective of this work was to specify the possibilities and needs of the training of Chemical Engineers in the University, with mastery of tools for scientific research, with a view to finding the optimal conditions for technology transfer. The analysis starts from the traditionally used analogies between impulse transfers, mass heat transfers, their dimensionless groups and design of experiments. Mathematical modeling is included to obtain information on real transport phenomena and the possibilities of scaling facilities in the chemical industry. The need for adequate experimental support for the decision-making proposal is reinforced and how through modern cybernetic methods responses to the demands of the industry can be reached more quickly. The significance, as a working instrument, of the incorporation of these methods in the scientific training of chemical engineers is emphasized.

Keywords – Design of experiments, Optimal conditions, Technology transfer

1. Introducción

Los procesos de la industria química y fermentativa tienen como objetivo fundamental lograr productos de alto valor agregado. Con ese propósito, se utilizan materias primas fundamentales, insumos químicos auxiliares, recursos energéticos, fuerza de trabajo e instalaciones de procesos industriales que han requerido un costo de adquisición y gastos inversionista, de manera que los recursos financieros, son requisitos indispensables para lograr los objetivos primarios en industrias de procesos. Además, como se conoce, este sector es fuente de residuos de agresividad al medio ambiente y la minimización de este efecto debe considerarse. El mundo moderno exige de los

dirigentes industriales el empleo de ideas nuevas para incrementar al máximo la eficiencia en la utilización de los recursos. Por ello, se comprende que cualquier idea que tienda a reducir gastos en la industria es, hoy por hoy, una fuerza que actúa positivamente sobre la eficiencia económica [1].

La economía actual representa un sistema extraordinariamente complejo, formado por multitud de eslabones, los cuales influyen directa e indirectamente unos en los otros. Con ello, la dirección de toda la economía y de sus eslabones individuales; estos últimos se hacen cada vez más difíciles dada la variedad de posibles decisiones de producción que se toman en los diferentes niveles. En esta época de internacionalización del conocimiento “la eficiencia mayor del trabajo y la rentabilidad máxima de la producción son efecto de soluciones científicas de nuevo tipo, adquiriendo particular importancia, las cuestiones de la búsqueda científica de decisiones óptimas para diferentes situaciones económicas” [1] [2].

Una nueva idea requiere de un proceso de experimentación para validar la tendencia real del comportamiento en la práctica tecnológica. Así, desde la concepción de esa idea hasta su introducción y adaptación a las condiciones del mundo productivo real, se requieren varios pasos que incluyen el escalado de las tecnologías hasta nivel industrial, lo que implica también, varias etapas y la obtención de información de variables químico-físicas requeridas para el diseño industrial.

Todo esto implica gastos de recursos materiales, humanos, financieros de equipamiento y de tiempo. Esta es quizás la menos considerada, pero la más importante, como se ha dicho, el tiempo es el único recurso que no se recupera y lo más preciado de que disponen aquellos que solo tienen a su talento como recurso.

En las condiciones actuales de Cuba, para reactivar la economía nacional, no solo se dispone de mucho tiempo, sino que tampoco se puede perderlo, por lo que se impone tomar las medidas requeridas para alcanzar las decisiones óptimas entre las nuevas tecnológicas, que se transfieran al sector de la economía nacional como demanda concreta de la industria química. Solo con esa impronta nuestra ciencia se podrá convertir en una fuerza productiva más. La idea sobre cómo alcanzar este propósito, descansa en concebir el núcleo básico de la metodología de investigación, las herramientas disponibles y su combinación para alcanzar rápidamente propuestas viables en el contexto de sector de la industria de procesos químicos y fermentativos, pues sin respuestas rápidas y seguras no habrá transferencia de conocimientos del sector de su generación hacia el de su aplicación en un adecuado vínculo universidad-empresa [2]. Para ello se deben encaminar los esfuerzos y la formación de grado y posgrado de nuestros educandos y ¿por qué no?, de nosotros mismos, los educadores. Las actividades de postgrado son de extremado interés, pues permiten la capacitación de recursos humanos como actores presentes y futuros de la comunidad científica en los diferentes sectores industriales aplicando herramientas modernas de investigación que aceleran la generación y evaluación de la transferencia de conocimientos a la economía nacional. La ciencia y la introducción de los resultados científicos en la producción, adquieren relevantes funciones sociales por lo que deberán estar orientadas al desarrollo armónico y proporcional de la ciencia de manera que contribuya al desarrollo integral de la técnica, la producción y la economía [3].

Por ello el objetivo de este trabajo fue precisar las posibilidades y necesidades de la formación de Ingenieros Químicos con dominio de las herramientas para la investigación científica, con vistas a encontrar las condiciones óptimas para la transferencia de tecnología.

2. Desarrollo

2.1. Necesidad del respaldo experimental

El desarrollo de la industria de procesos químicos se ha fundamentado en el uso intensivo de métodos experimentarles, descansando en una concepción insigne de cómo percibir los fenómenos de transporte basado en las tradicionalmente utilizadas analogías entre las transferencias de impulso, de calor y de masa. No obstante, lo avanzado, los nuevos desarrollos industriales, utilizando diferentes tipos y calidades de materias primas, reclaman, sobre todo en las condiciones del reto de la asimilación y adecuación de las nuevas tecnología a las condiciones especificas de Cuba, que los centros de generación de conocimientos garanticen información en sus laboratorios que sirvan de respaldo a las decisiones inversionistas, no solo para tecnologías propias, sino también para las tecnologías foráneas que se propongan.

Una simple observación experimental en un laboratorio, o a escala piloto puede evitar gastos de inversión improductivos. No obstante, lo anterior, como se ha dicho, el experimento ha sido siempre una gran herramienta en la solución de problemas prácticos y la verificación de hipótesis en la industria de procesos químicos. [3].

Los métodos tradicionales de experimentación implican un considerable esfuerzo, tiempo y recursos para su ejecución elevando los costos de los resultados investigativos, sobre todo si son necesarios realizarlos a nivel de planta piloto o industrial. La investigación puede obtener información sobre el fenómeno estudiado, para después actuar sobre el mismo; también puede definirse la eficiencia de la investigación como la cantidad de información útil obtenida por unidad de costo, por consiguiente, es extremadamente importante utilizar métodos experimentales que le brinden la máxima cantidad de información con el menor costo y esfuerzo.

En la época actual, para acelerar los resultados y enfoques multilaterales de las investigaciones, los modernos métodos matemáticos se han convertido en un poderoso arsenal metodológico para la solución actual y prospectiva [4].

2.2. El uso de los métodos de diseño de experimento

El uso del Diseño de Experimento (DE) estadístico facilita un incremento apreciable en la productividad de los investigadores, así como la confiabilidad de los resultados obtenidos, siendo estos métodos por su naturaleza universal aplicables en la mayoría de los campos de investigación y significa una gran contribución a la optimización de la experimentación. No es necesaria una preparación especial en estadísticas o matemáticas para utilizar estos métodos, la experiencia ha demostrado que los ingenieros comprenden y aplican con éxito sus fundamentos.

La idea de que un experimento se puede diseñar, es de tiempos antiguos, sin embargo, sólo a principios del presente siglo, se introdujeron los métodos estadísticos de DE. En la década de los años cincuenta se inició una nueva etapa en los trabajos de DE encaminando los esfuerzos a encontrar las condiciones óptimas [5].

El uso del DE facilita un incremento apreciable de la productividad de los investigadores y de la confiabilidad de los resultados obtenidos, en general se puede afirmar que si los experimentos se planifican incorporando diseños estadísticos factoriales o diseños factoriales parciales la información obtenida es confiable y tiende a minimizar el número de experimentos necesarios. Sin embargo, si la planificación de las experiencias se hace deficientemente, sin tener en cuenta los aspectos específicos del análisis, generalmente no se podrá reunir mucha información útil. [6]

Esto se debe a que de los experimentos planificados deficientemente no se obtiene la información principal, lo que refuerza la necesidad de la adecuada formación del profesional desde el pregrado en esta dirección y una comprensión de que en estos aspectos reside el núcleo básico de la metodología de la investigación en la industria de procesos químicos y el éxito de sus funciones profesionales esenciales, es decir el control e intensificación de los procesos establecidos y el desarrollo de nuevos procesos, por lo que es esencial en la formación del ingeniero químico.

En muchas investigaciones se plantean los interrogantes siguientes:

1.- Qué variable(s) afecta(n) la(s) respuesta(s)?

2.- De qué forma se afecta(n) la(s) respuesta(s)?

Se ha demostrado en la experiencia investigativa que experimentos desarrollados de forma simple pueden dar respuesta a ambas preguntas.

Los métodos de optimización permiten determinar la forma que se hacen las cosas en uno y otro nivel de desarrollo científico. Sin embargo, los métodos matemáticos de optimización, por su propia naturaleza, no pueden ser aplicados de forma directa a la realidad estudiada, sino a modelos matemáticos de determinado conjunto de manifestaciones del fenómeno estudiado, los que al ser estudiados, solo presentan un nivel práctico si los mismos reflejan de un modo adecuado, las situaciones reales y satisfacen determinado grado de exactitud.

Según la complejidad de los sistemas se requerirá mayor o menor información, para obtener el mayor o menor trabajo experimental. El esfuerzo de muchos investigadores durante los años de aplicación de estos métodos se ha contribuido a optimizar el trabajo experimental reduciendo los tiempos y esfuerzos para obtener resultados, siendo válido el análisis propuesto en la Tabla 1.

Tabla 1. Rango de utilización de los tipos de diseño experimental según la cantidad de factores.

Diseño experimental	Variables independientes para ser investigadas 2 3 4 5 6 7 8 9 10 11 >11
Modelos gráficos	2 3	4
Factorial completo	2 3 4			5
Factorial parcial			4	5 6 7 8		9
Factorial parcial saturado				5	6 7 8 9 10 11 >11

*La zona gris clara significa la zona de la aplicación menos usada para el diseño experimental.

Fuente [7][8]

La extraordinaria capacidad de reducir trabajo experimental mediante la planificación experimental, apoyado en los métodos modernos de diseño experimental (Tabla 2), permiten incorporar, a la labor investigativa, a personal en formación, sin temor a perder información por errores experimentales, que siempre se pueden detectar induciendo, si es requerido, las repeticiones de pocos ensayos.

Tabla 2. Comparación entre diversos repliegues parciales y el correspondiente diseño factorial completo

Nro. de Factores	Número de Ensayos
Nro. de Factores	Repliegue fraccional	Símbolo	Diseño parcial	Diseño factorial
3	1/2 repliegue de 2³	2 ^3-1	4	8
4	1/2 repliegue de 2⁴	2 ^4-1	8	16
5	1/4 repliegue de 2⁵	2 ^5-2	8	32
6	1/8 repliegue de 2⁶	2 ^6-3	8	64
7	1/16 repliegue de 2⁷	2 ^7-4	8	128
5	1/2 repliegue de 2⁵	2 ^5-1	16	32
6	1/4 repliegue de 2⁶	2 ^6-2	16	64
7	1/8 repliegue de 2⁷	2 ^7-3	16	128
8	1/16 repliegue de 2⁸	2 ^8-4	16	256
9	1/32 repliegue de 2⁹	2 ^9-5	16	512
10	1/64 repliegue de 2¹⁰	2 ^10-6	16	1024
11	1/128 repliegue de 2¹¹	2 ^11-7	16	2048
12	1/256 repliegue de 2¹²	2 ^12-8	16	4096
13	1/512 repliegue de 2¹³	2 ^13-9	16	8192
14	1/1024 repliegue de 2¹⁴	2 ^14-10	16	16348
15	1/2048 repliegue de 2¹⁵	2 ^15-10	16	32768

Fuente [8] [9]

La utilización de estos métodos formalizados permite por su estructuración el trabajo en equipos, incluyendo profesionales de reciente graduación y estudiantes, incluso experimentos en condiciones industriales [9] y reafirman el papel de la formación en las Ciencias Básicas en la formación de investigadores [10].

2.3. La modelación matemática herramienta imprescindible para el Ingeniero Químico

Un modelo matemático se define, de manera general, como una formulación o una ecuación que

expresa las características esenciales de un sistema físico o de un proceso en términos matemáticos.

Los modelos tienen dos propósitos básicos, con formas fundamentales y de acuerdo con estos

propósitos pueden ser [11]:

a. Modelos dinámicos, tipo de ecuaciones generalmente diferenciales, para los estudios de

control automático y afines.

b. Modelos estáticos, tipos de ecuaciones generalmente algebraicas, para estudios de diseño

técnico y optimización técnico económica.

La forma y uso de los modelos también determinan indirectamente los límites de su tamaño

físico en términos de número de variables que se estimen y la cantidad de ecuaciones implicadas,

así como el tamaño y la complejidad de los medios físicos que se consideren. La descripción cuantitativa de los sistemas de procesos, es una de las tareas de interés en la actualidad, para lograr este objetivo, una de las condiciones previas, es que la cantidad de información disponible permita describir, las relaciones entre los elementos y dentro de los elementos, de manera que con el modelo obtenido de un sistema real, se pueda en determinada etapa del proceso del conocimiento sustituir al sistema real, y por medio de su investigación y estudio obtener la información deseada sobre el sistema real, por ello, la calidad de un modelo matemático está determinada por la precisión con que coincidan los procesos en el sistema real con los procesos obtenidos mediante el modelo, y debe existir [11]:

· Concordancia objetiva con el propio sistema;

· Posibilidad de sustituir el sistema en el proceso del conocimiento;

· Propiedad de suministrar información práctica sobre el sistema;

· Determinadas reglas mediante las cuales la información del modelo pueda transformarse en

información del sistema.

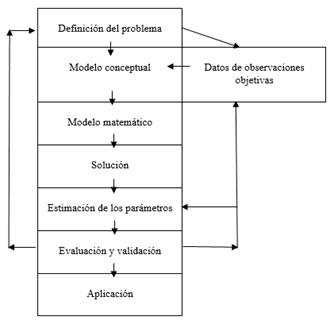
En la Fig.1 se presenta el Diagrama Heurístico para la confección de un modelo matemático.

Fig 1. Diagrama Heurístico para la confección de un modelo matemático[U1] .

Fuente: elaboración propia (2020)

La visión abarcadora y pormenorizada que exige un modelo dinámico es un factor clave para que los profesionales en los estudios de grado y postgrado, profundicen en el conocimiento real de los procesos tecnológicos en estudio, haciendo hincapié en las aplicaciones de las leyes de semejanza de los fenómenos de transporte de impulso, calor y masa con una visión más completa que lo realizado con los métodos tradicionales por lo que son un elemento esencial en la formación de los profesionales de la Ingeniería Química.

Para el diseño y construcción de equipos industriales (prototipos), existen dos caminos posibles, que pasan por la construcción de modelos. Estos modelos pueden ser matemáticos o empíricos.

Modelos matemáticos: a partir de de aspectos teóricos es posible, a veces, diseñar y construir directamente un prototipo, aplicable a escala industrial. En la práctica esto se presenta en contadas ocasiones.

Modelos empíricos: en estos casos se necesita de experimentación en modelos reducidos o maquetas, siguiendo las directrices dadas por el análisis dimensional.

A partir de los valores encontrados en el modelo, se calculan los valores del prototipo. Para pasar del modelo al prototipo se deben cumplir una serie de criterios de semejanza. La diferencia primordial entre los dos modelos estriba en que el matemático es aplicable a cualquier escala, mientras que, para la aplicación del modelo empírico se deben cumplir una serie de criterios de semejanza entre el modelo y el prototipo.

De modo general, el criterio de semejanza puede expresarse según la ecuación lineal:

(1)

Donde:

m y m` son las medidas de una misma magnitud en el modelo y en el prototipo, respectivamente.

k = es el factor de escala (cte.de proporcionalidad)

Este principio de semejanza es aplicable a las distintas magnitudes que engloban el sistema. Por tanto los distintos criterios de semejanza serán:

Semejanza geométrica: referidas a la proporcionalidad entre las dimensiones del modelo y el prototipo.

Semejanza mecánica: que puede ser estática, cinemática y dinámica, según se refiera a la proporcionalidad entre las deformaciones, velocidades y fuerzas, respectivamente.

Semejanza térmica: si existe proporcionalidad entre las temperaturas.

Semejanza de concentración: referida a la correspondencia en todo proceso químico, que obliga a la proporcionalidad entre las concentraciones y composiciones.

La semejanza geométrica es requisito previo para todas las demás. En general cada una de ellas, resulta requisito para todas las demás. [12]

3. Resultados y Discusión

3.1 Nuevo paradigma del diseño de procesos de la industria química.

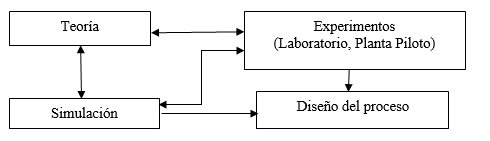
La solución del modelo matemático del proceso, una vez confeccionado, conlleva la verificación del ajuste de los parámetros desconocidos o inciertos del modelo y su validación en la región de experimentación, a fin de conocer su potencialidad predictiva. Para ello hay que desarrollar experimentos que previamente deben ser diseñados cuidadosamente a fin de establecer la región de experimentación adecuada y las variables que deben ser consideradas en la experimentación. En la Figura 2 se presenta el nuevo paradigma del diseño de procesos para el siglo XXI, aquí puede ser visualizado con un enfoque holístico.

Fig. 2. Nuevo paradigma del diseño de procesos para el siglo XXI

Considerando que el patrón de flujo del proceso puede ser alterado con el cambio de escala, la experimentación debe realizarse en la escala más cercana posible al prototipo o debe tenerse muy presente este aspecto para aplicar el modelo matemático a una escala diferente. Para el ajuste de los parámetros del modelo frecuentemente se utiliza el método de la regresión no lineal múltiple. La utilización de la computación en la solución de estos sistemas es obligada, a fin de obtener soluciones confiables y en el menor tiempo posible.

Los balances se realizan considerando los términos de entrada, salida y acumulación de masa, de energía o de cantidad de movimiento respectivamente. En forma de ecuación genérica se presentan las siguientes ecuaciones:

(2)

Donde:

Cantidad puede ser: masa o energía o cantidad de movimiento.

Las expresiones generales resultantes son las siguientes:

Balance total de masa (sin reacción química):

(3)

Donde:

V es el volumen (m³),

r es la densidad (kg/m³)

F es el flujo (m³/h)

i para las corrientes de entrada

j para las corrientes de salida.

Balance de componente con reacción química:

(4)

Donde:

Ca es la concentración del componente (mol/m³)

V es el volumen (m³)

F es el flujo (m³/h)

r es la transformación por reacción química en mol/(m³ h)

A_t es el área de transferencia (m²)

J es el flujo transferido en mol/(m² h)

Balance de energía:

(5)

Donde:

E es la energía interna (U) + la potencial (P) + la cinética (K), todo en (kJ),

h es la entalpía (kJ/kg)

Q es la energía transferida (kJ/h)

Ws es el trabajo realizado por o entregado al proceso

Una vez confeccionado el modelo este puede ser utilizado para la solución de cualquiera de los problemas particulares que debe resolver un Ingeniero Químico, ya sea el de diseño (o síntesis), el de análisis o el de control. Todos pueden ser resueltos integralmente, mediante el planteamiento del problema general de la Ingeniería Química, como un problema único, a partir de una formulación integral de este, como problema de optimización multiobjetivos de un sistema matemático de ecuaciones.

4. Conclusiones

Es necesario incrementar aceleradamente la capacidad de obtención y procesamiento de información incorporando todo el respaldo de la Universidad en general.

La aplicación de los modernos métodos matemáticos son una vía adecuada para el procesamiento acelerado de información para la propuesta de decisiones de desarrollo de la industria química.

La formación en la utilización práctica y sistemática de las herramientas matemáticas es un rasgo distintivo de la época en lo referente a la formación de pregrado y postgrado del Ingeniero Químico

Referencias

[1] Y. Adler, Yu. Markova, V. Granovkyl "The Design of Experiment of Find Optimal Conditions". MIR, Moscow 1975, pp.102.

[2] Box, G.E.P.; T. S. Hunter, "The 2^{k -p} Factorial Designs". Technometric (8): 311- 352, 1961.

[3] E.González Suárez, W. F. Quezada Moreno, I. Y.González Herrera, D. N. Concepción Toledo, Miño Valdés

J.E. (2018). “Gestión del conocimiento para la industria química y fermentativa con apoyo de la optimización”

EdUNaM. ISBN: 978-950-766-133-4, Posadas 2018 González et al, 2018

[4] Box, G.E.P.; K. B. Wilson,:"On ther Experimental Design Attaimeat of optimum Condition" Journal Rev. Stat. Soc. (1951) 13 .

[5] V.Kafarov, “Problemas científicos actuales en la Ingeniería Química”. Control, Cibernética y Automatización. Año VIII, Nro 4, La Habana, 1974, pp 38-47.

[6] L.Kantorovich, A.B. Gorstico. “Las decisiones optimas en la economía”. Editorial de ciencias sociales. Ciudad de la Habana, 1979, pp.7-8

[7] W.B. Isaccson, "Statistical Analyses for Multivariable Systems".Chem Eng., (6): 69-75, 1975.

[8] E.González Suárez, J.E.Miño Valdés, D.Concepción Toledo “La planificacin experimental de nuevas tecnologías para la obtención de productos químicos” en Gestión de Conocimientos en la Estrategia de Desarrollo de la Industria de Caña de Azúcar en el Concepto de Biorefinería. Ed.Gráfica Libertad, pp.69-71, Posadas Arg 2019.

[9] E.González Suárez, “La influencia de las ciencias básicas en la formación de investigadores de Cuba”. Revista Nómadas. Sept.1997. Nro.7. Fundación Universidad Central. Santafé de Bogotá, Colombia 1997.

[10] A.Rasmuson, B. Andersson, L. Olsson, R. Andersson. “Mathematical Modeling in Chemical Engineering” Chalmers University of Technology,Cambridge University Press 2014.

[11] R.Cortés Martínez et al., “Modelación y simulación de procesos en la intensificación de instalaciones de la

industria química”, +Ingenio Vol.2 Nro.2, pp.22-36, dic.2020

[12] A.Ibarz, G.Barboza-Cánovas “Análisis dimensional y semejanza” en Operaciones Unitarias en la Ingeniería de los Alimentos. Ed.Mundi-Prensa Madrid, España 2015, pp 46-48.