1.
Introducción
Se denomina microrredes (microgrids) a los
sistemas de Generación Distribuida (GD) conformados por un conjunto de unidades
de generación, típicamente paneles fotovoltaicos, turbinas eólicas, micro
turbinas; unidades de almacenamiento y cargas, estando estos elementos
interconectados a través de interfaces electrónicas de potencia y un sistema de
comunicación [1].
Comúnmente, una microrred adapta a las
fuentes que la conforman, a las necesidades de frecuencia y tensión del lugar
donde se encuentra instalada, siendo en Argentina, 220 V y 50 Hz. Por tanto,
por esta diversidad de fuentes de energía, la microrred debe gestionar, en
forma automática y rápida, los niveles de corriente y tensión para mantener la
alimentación de la carga en un nivel estable, y dentro de esta gestión, se
encuentra conectar en paralelo inversores estáticos de potencia, los cuales
hacen de interfaz electrónica entre las fuentes de energía y la red de CA
(corriente alterna) que se interconecta al sistema de distribución
convencional.
En este ámbito cobran importancia las
estrategias de control por curva de caída (droop control) [2], las cuales se
basan en emular ciertas características del funcionamiento de los generadores
síncronos en el sistema de potencia, con el objetivo de lograr el sincronismo
entre los inversores sin necesidad de tener un convertidor o la red eléctrica
que imponga la frecuencia en el sistema [3], ni utilizar comunicación de datos
entre los inversores.
La principal desventaja del control por
curva de caída es que existe una corriente de circulación entre inversores.
Para minimizar dicha corriente, es posible modificar la impedancia de salida de
cada inversor; para esto existen dos opciones: (1) introducir inductores a la
salida de los filtros LC de cada inversor (lo cual incrementa el volumen y
costo del inversor), o (2) incorporar en el algoritmo de control un lazo de
impedancia virtual [4].
Por otro lado, el efecto que el lazo de
control de tensión tiene sobre la impedancia de salida del inversor, es el de
reducirla en la frecuencia fundamental y las frecuencias armónicas para lograr
buena regulación de tensión y reducida distorsión armónica cuando se alimentan
cargas no lineales. Para lograr esto utilizando controladores del tipo proporcional
+ integral + derivativo (PID), es necesario introducir elevadas ganancias que
representa un problema en términos de estabilidad relativa, especialmente
cuando estos controladores son implementados en sistemas digitales [5], ya que
los atrasos de transporte que existen entre el muestreo de las señales y la
actualización de la acción de control reducen significativamente los márgenes
de estabilidad del sistema.
Para solucionar estos problemas, diversos
autores han propuesto el uso de controladores basados en el principio de modelo
interno (IMP - internal model principle) [6], los cuales se diseñan para
actuar con elevadas ganancias solamente en las frecuencias donde se desea
obtener reducción de impedancia de salida y seguimiento de referencias,
consiguiendo amplios márgenes de estabilidad y elevada robustez ante incertezas
paramétricas [7]. Como desventaja de los controladores basados en el IMP, las
dos formas más generales de implementación, ya sea por controladores resonantes
[8] o repetitivos [9], requieren de una considerable cantidad de recursos
computacionales, principalmente cuando se requieren alimentar cargas no
lineales, ya que estas consumen una corriente con elevada distorsión armónica
que produce perturbaciones sobre la tensión de salida en frecuencias múltiples
de la componente fundamental, típicamente hasta el armónico número 15 [7].
En el presente trabajo, se utiliza la
acción integral como controlador de amplio ancho de banda para el control de la
tensión de salida. Para establecer los límites de la ganancia de este
controlador, se propone realizar un análisis de robustez del sistema a lazo
cerrado, utilizando como variación paramétrica la inductancia del filtro LC, el
cual es el parámetro que más afecta a la estabilidad ya que varía significativamente
con la temperatura de este componente [10].
De las propuestas existentes en la literatura científica
para implementar lazos de impedancia virtual [11], se escogió para esta
propuesta, la que consiste en un lazo interno de control de corriente con
controlador proporcional y un lazo externo de tensión con un simple controlador
integral. En el lazo de impedancia virtual se implementa directamente la
dinámica de un circuito RL, el cual permite limitar el comportamiento inductivo
a alta frecuencia [12]. La presencia de la componente inductiva a baja
frecuencia provoca una componente de corriente continua en la corriente del
inductor del filtro LC, provocando incrementos de temperatura en el circuito
magnético del inductor, con las consecuencias ya conocidas. Se propone en este
artículo una solución para reducir esta componente CC en base a una simple
modificación de la acción integral del lazo de tensión. Se presenta un
procedimiento de diseño de toda la estrategia, tanto para los controladores como
para la impedancia virtual, y esta propuesta se valida mediante resultados de
simulación. Finalmente se describen los trabajos futuros que se pretenden
explorar a partir de lo realizado hasta el momento.
2. Descripción del sistema
2.1.Descripción de los convertidores
estáticos de potencia
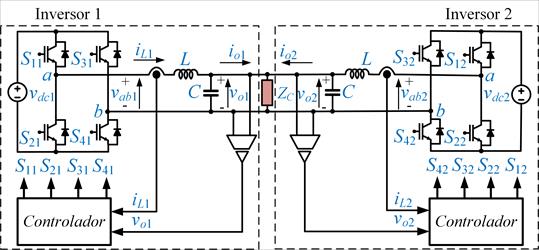
En la Fig. 1. se observa el circuito
eléctrico de dos inversores monofásicos conectados en paralelo y, funcionando
en modo aislado de la red eléctrica.
Fig. 1.
Representación
de inversores monofásicos en paralelo, cargas y principales variables del
circuito.
En la Tabla 1 se muestran parámetros de
cada inversor.
Tabla 1. Parámetros
del inversor monofásico.
|
Parámetro
|
Símbolo
|
Valor
|
|
Potencia de salida
|
S
|
2 kVA
|
|
Tensión de entrada
|
Vdc
|
400 V
|
|
Tensión de salida RMS
|
Vac
|
220 V
|
|
Frecuencia fundamental
|
fr
|
50 Hz
|
|
Frecuencia de conmutación
|
fs
|
10 kHz
|
|
Inductancia filtro de salida
|
L
|
500 µH
|
|
Resistencia del inductor
|
rL
|
0,118 Ω
|
|
Resistencia carga nominal
|
Rc
|
24,2 Ω
|
|
Capacitancia filtro de salida
|
C
|
60 µF
|
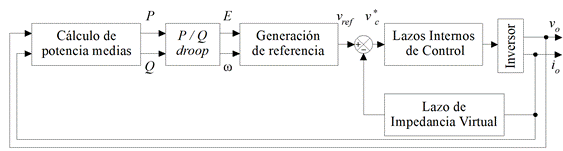
La Fig. 2. corresponde al diagrama de bloques general que utilizan las propuestas
de control por curva de caída.
Fig. 2.
Diagrama
de bloques general para implementar estrategias de control por curva de caída
mediante lazo de impedancia virtual.
Cada inversor está
compuesto por un puente de semiconductores IGBT (Insulated Gate Bipolar
Transistor), los cuales permiten obtener tensiones de corriente alternada vab1
y vab2 con contenido armónico de alta frecuencia
debido a la utilización de modulación PWM para el comando de las llaves, siendo
estas filtradas por filtros LC que poseen una frecuencia de resonancia
por arriba de la frecuencia fundamental que se desea obtener. En la Fig. 1. también se pueden
observar los sensores utilizados para obtener las variables a realimentar a los
controladores de cada convertidor, los cuales generarán las señales de disparo
de los IGBT de acuerdo a la estrategia de control que se describe a
continuación.
Dicha estrategia de control consta de
las siguientes etapas:
(i) Cálculo de potencia activa (P)
y reactiva (Q) que entrega cada inversor, a partir de la medición de la
tensión y corriente sobre la carga.
(ii) La característica de decaimiento
o pendiente de la curva de caída.
(iii) Generación del ángulo ω y
la amplitud E de la señal de referencia para los lazos internos de
control.
(iv) Lazo de impedancia virtual para
fijar la impedancia de salida deseada (Zv).
(v) Lazos internos de control, de
corriente y de tensión, que agregan amortiguamiento y características de
seguimiento de referencia, respectivamente.
(vi) Inversor alimentado en tensión,
que impone la tensión de salida vo y la corriente en la carga
io.
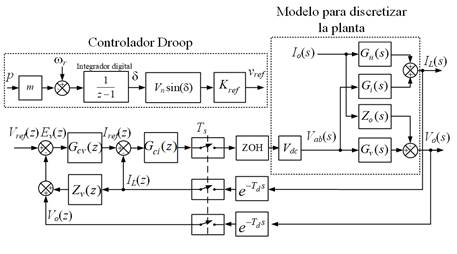
Debido a que el sistema
presenta lazos de control anidados, se determina la representación en diagrama
de bloques de la Fig. 3., con el objetivo de poder
discretizar la planta. Para esto, se ubican los bloques que modelan las plantas
correspondientes a cada lazo de control entre los bloques ZOH y de atraso de
transporte e-sT, los cuales se corresponden con
los efectos de la implementación digital (el primero es el efecto del retenedor
de orden cero y el segundo el atraso de implementación digital de la acción de
control). En este caso particular se considerará para el análisis T = Ti
= Tv = Ts. El tiempo de muestreo y
actualización de la acción de control, Ts = 100 µs.
Para determinar los
bloques que describen el comportamiento de la planta de la Fig. 3., pueden encontrarse las
funciones de transferencia (FT) Gv(s); Gi(s);
Gii(s) y Zo(s):
Estas FT, están asociadas físicamente
a las dinámicas del filtro LC a partir de las FT descritas en las
ecuaciones (1), (1) y (1).
|
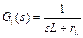 : FT del inductor : FT del inductor
|
(5)
|
|
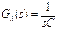 : FT del capacitor : FT del capacitor
|
(6)
|
|
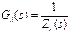 : FT de la carga : FT de la carga
|
(7)
|
Fig. 3. Diagrama de bloques del
modelo del inversor a lazo cerrado considerando los efectos de la implementación
digital y representación de la planta para su discretización.
Los siguientes bloques en
la Fig. 3. corresponden a
Gci(z): FT del
controlador de corriente; Gcv(z): FT del controlador
de tensión y Zv(z): FT de la impedancia de salida
deseada.
En la Fig. 3. se muestra el controlador
droop, donde el coeficiente m es proporcional a la potencia
activa, que al restarse con la pulsación fundamental wr debe integrarse para
obtener el ángulo d de la señal de referencia Kref Vn sen
(d). El coeficiente Kref corresponde a
la relación entre una tensión RMS de referencia (Vref) y la
tensión de salida del inversor en vacío (Vo_vacío), para obtener el valor
deseado de tensión en la salida.
|
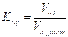
|
(8)
|
3.
Diseños
de los lazos de control
3.1.Lazos internos de control
El bloque Lazos Internos de
Control de la Fig. 2., está compuesto por los
lazos de corriente y de tensión. En la Fig. 1. se puede observar que son
controladas la corriente en el inductor del filtro y la tensión en el
capacitor. Para realizar la compensación de la corriente en el inductor, se
propone utilizar una acción proporcional, la cual tiene el objetivo principal
de mejorar la estabilidad relativa del sistema. La FT de este controlador es: Gci(z)
= Kp, donde Kp es la ganancia proporcional.
Debido a que el controlador será
implementado en un microcontrolador, se realiza un análisis en tiempo discreto
de la planta utilizando la transformada Z modificada, la cual permite tener en
cuenta el atraso de transporte T (tiempo entre el muestreo de las
variables y la actualización de la acción de control). En base a esto, las FT
muestreadas de (1) y (1)
resultan:
|
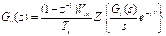
|
(9)
|
|
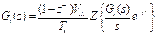
|
(10)
|
También es factible
utilizar un tiempo de atraso de transporte de 50 µs (media muestra) ya que, al
utilizarse un lazo de control de corriente con una acción de control
proporcional, y un lazo de control de tensión con una acción integral, la
implementación de la estrategia de control no es tan costosa
computacionalmente como un controlador resonante [8].
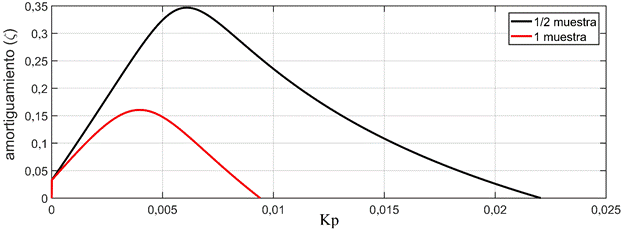
Utilizando el software
MATLAB se analizaron los lugares de raíces de la planta, implementándose
atrasos de 1/2 muestra y de 1 muestra. Se graficó el amortiguamiento variando Kp
para obtener la evolución de estos parámetros, en ambos casos de atrasos como
se muestra en la Fig. 4.
Fig. 4. Amortiguamiento para
distintos valores de Kp y atraso de 1 y de 1/2
muestra.
Como se puede observar en
la Fig. 4., la ventaja de
implementar un controlador con un atraso de transporte de 1/2 muestra, es
obtener un mayor amortiguamiento, por lo que se opta por utilizar este esquema
de muestreo de las variables a controlar y actualización de la acción de
control.
Con el objetivo de
disminuir significativamente la impedancia de salida, lo cual se traduce en
aumentar el rechazo a las perturbaciones y lograr un seguimiento de la
referencia a la frecuencia de interés (en este trabajo se considerará
únicamente 50 Hz), se propone un controlador de tensión del tipo integrador,
que permite introducir una ganancia elevada en torno a la frecuencia
fundamental.
Donde Ki es la
constante integral, Ts el período de muestreo y z es
la variable discreta.
Para ver el efecto en la
FT de lazo abierto luego de agregar el control de tensión, se determinan dos
funciones de transferencia: una correspondiente al sistema a lazo abierto sin
controlador de tensión, Gvla(z), y la otra incluyendo
el controlador de tensión, Gcvla(z):
|
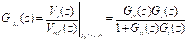
|
(12)
|
|
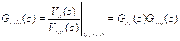
|
(13)
|
En la Fig. 5. se observa el lugar de
raíces de la planta a lazo abierto Gvla(z) y en la
misma gráfica se incluye el lugar de raíces de Gcvla(z)
con el compensador de tensión, pudiéndose apreciar como el controlador modifica
la trayectoria de las raíces del sistema.
Fig. 5. Lugar de raíces de Gvla(z)
y Gcvla(z).
El lugar de raíces con
controlador integral obtenido corresponde a la variación de Ki
en el rango de 0 a infinito, mostrándose solamente en el gráfico la región en
torno al círculo unitario. A partir del gráfico de la Fig. 5., es posible fijar una
ganancia que se encuentre dentro de los límites del círculo unitario, además de
explorar los límites para obtener un comportamiento con el mayor
amortiguamiento posible para los polos dominantes del sistema, lo cual se
indica con el valor de 0,0496 correspondiente a la ganancia del controlador
para la ubicación de los polos en ese punto.
Debido a que el objetivo
del lazo de control de tensión es lograr el seguimiento de la referencia y el
rechazo de perturbaciones, se analiza el efecto que Ki
presenta sobre la impedancia de salida del inversor en el rango de ganancias (KiTs)
de 0 hasta 0,1842 y poder establecer un criterio para la selección de Ki.
A partir de simulaciones numéricas es posible determinar que, ganancias por
arriba de 0,005 logran valores de impedancia de salida tales, que, al conectar
una carga, la regulación del inversor se mantiene dentro de los límites
establecidos por las normas de calidad de energía (± 10%).
En cuanto a la
determinación del límite superior para la ganancia Ki, se
propone analizar la robustez del sistema ante una variación del valor de la
inductancia del filtro LC, por ser este parámetro el que mayor impacto
tiene sobre la estabilidad del sistema, ya que variaciones en la temperatura
del inductor pueden causar significativa reducción de la permeabilidad del
núcleo. Para el análisis de robustez se debe establecer la ganancia del
controlador dentro de los valores que logran estabilidad en el sistema, para
luego encontrar los límites de variación paramétrica que logran mantener los
polos dentro del círculo unitario del plano Z.
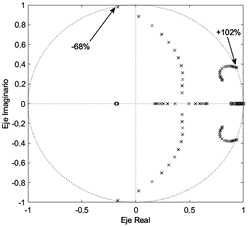
En la Fig. 6. se presenta el lugar de
raíces del sistema donde se produjo una variación de la inductancia del filtro LC
desde -68% a +102%. Fijando la ganancia Ki en 1000.
Fig. 6. Diagrama de polos y ceros del
sistema a lazo cerrado para una variación de la inductancia del filtro LC.
El mismo análisis
se realizó para distintos valores de Ki permitiendo obtener
el rango de variación permisible de la inductancia como se muestra en la
Tabla 1. Límites
De Variación Del Inductor Del Filtro Lc Para Distintos Valores De Ki
|
Ki
|
Límite
Inferior
|
Límite
Superior
|
|
900
|
-68%
|
+124%
|
|
1000
|
-68%
|
+102%
|
|
1100
|
-68%
|
+80%
|
|
1200
|
-68%
|
+65%
|
|
1300
|
-68%
|
+51%
|
De este análisis se
concluye que el cambio en la ganancia integral del controlador de tensión solo
afecta el límite superior de variación de la inductancia, por lo que sabiendo
que es más probable que esta variación paramétrica sea decreciente, la robustez
del sistema está garantizada independientemente del valor de Ki.
En función del análisis realizado para el diseño del lazo de control de tensión
con controlador integral, considerando los parámetros nominales resumidos en la
Tabla 1, se escogió para el
análisis por simulaciones numéricas Ki = 1000, observándose
los efectos de esta ganancia sobre la impedancia de salida en la siguiente
sección.
3.2.Lazo de impedancia virtual
El bloque lazo de
impedancia virtual de la Fig. 2., tiene como objetivo
permitir establecer valores específicos de amplitud y fase de la impedancia de
salida para lograr el correcto funcionamiento de la estrategia de control por
curva de caída (droop), evitando así un inductor de línea (inductor
físico entre inversores conectados en paralelo) para realizar dicho control.
Existe una relación de compromiso en la selección de su magnitud, ya que
valores elevados de la impedancia de salida producen una regulación
desfavorable en la tensión de salida. Por otro lado, una baja impedancia de
salida favorecerá mayores corrientes de circulación en el caso de
funcionamiento en paralelo de dos o más inversores.
Como se puede ver en la Fig. 2., la señal de salida del
bloque de impedancia virtual modifica la señal de referencia del lazo externo
de control de tensión del inversor, donde la tensión de referencia modificada Vref*
se obtiene de la diferencia entre el valor de referencia obtenido a partir de
las ecuaciones del controlador droop y la caída de tensión virtual a través de la
impedancia virtual:
|
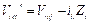
|
(14)
|
A diferencia de lo que se
observa en la Fig. 2., en lugar de utilizar io
para producir la caída de tensión debido a la impedancia virtual, en este
trabajo se utiliza la corriente iL, ya que es posible
utilizar esta variable para disminuir el número de sensores en la
implementación de la estrategia de control.
Para el diseño se debe
tener en cuenta que Zv debe ser significativamente mayor a la
impedancia de salida obtenida mediante los controladores de lazos internos a la
frecuencia fundamental, de forma tal que Zv logre imponer su
característica sobre la impedancia de salida. Con esto se logra el correcto funcionamiento
del droop, ya que Zv logra desacoplar los flujos de
potencia activa y reactiva en el sistema. Esto permite que, para el caso de una
impedancia reactiva a frecuencia fundamental, el flujo de potencia activa
dependa del ángulo entre las tensiones de cada inversor, mientras que la
potencia reactiva, dependa de la diferencia de amplitud entre estas tensiones.
En caso de una impedancia resistiva, este comportamiento para cada potencia se
invierte.
La característica de
impedancia a utilizar depende de diversos factores. Varios autores sugieren
aprovechar las características de las impedancias de los cables que separan a
los inversores, ya que la impedancia de salida se sumaría a esta para lograr la
característica deseada. Otra forma de escoger el tipo de impedancia es en
función de la componente de potencia que se quiere eliminar de la corriente de
circulación, ya que una impedancia reactiva logra el sincronismo entre los
inversores mediante variaciones en las potencias activas, logrando en el estado
de equilibro que la potencia activa entregada por cada inversor sea la misma.
Mientras que, en el caso de una impedancia resistiva, el sincronismo se alcanza
cuando las potencias reactivas de cada inversor sean iguales.
La regulación de tensión
es un tercer factor por considerar, ya que, dependiendo de la característica de
impedancia de salida, la regulación de tensión resulta más favorable en casos
de impedancia reactiva en comparación con resistiva, inclusive una impedancia
capacitiva presenta mejores resultados que una inductiva.
Debido a que la
utilización de una acción integral en el lazo de control de tensión produce una
impedancia de salida con característica predominantemente inductiva, la
utilización de un inductor virtual facilita imponer una característica de fase
predominantemente inductiva, por lo que se utilizará este tipo de impedancia
virtual. Una de las formas más simples para lograr implementar una impedancia
virtual predominantemente inductiva, es mediante la siguiente FT.
|
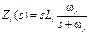
|
(15)
|
Esta FT resulta de la
combinación de la FT del inductor virtual con un filtro pasa bajos, teniendo
este último el objetivo de limitar el efecto del lazo de impedancia virtual en
las frecuencias de los polos dominantes de los lazos internos del sistema,
además de evitar la amplificación de ruidos que provienen de la medición de
corriente del inductor.
Para el análisis por
simulaciones numéricas se tomó un valor de ωc = 900
rad/s, estableciéndose una frecuencia de corte lo suficientemente alejada de la
pulsación fundamental. En cuanto a la magnitud de la impedancia virtual, ésta
se ajustó mediante el parámetro Lv tomando un valor de 2,8
mH, con el objetivo de aumentar la impedancia de salida y lograr un
comportamiento inductivo a la frecuencia fundamental.
Para observar el efecto
del lazo de impedancia virtual sobre la impedancia de salida, se debe
determinar la FT de la función de rechazo de perturbación del sistema; lo que
equivale a la impedancia de salida total del mismo. Esta FT, dada por la
relación entre Vo(z) e Io(z)
con Vref(z) = 0, la cual puede obtenerse de la Fig. 3., y además, en la misma,
se debe incluir Zv(z):
|
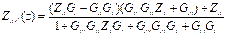
|
(16)
|
Para obtener la FT de
tiempo discreto de la impedancia virtual y de las funciones Gii(s)
y Zo(s), se propone, para análisis comparativo,
realizar la discretización mediante un retenedor de primer orden, el cual
consigue un comportamiento en frecuencia similar a la FT de tiempo continuo.
Los efectos del lazo de
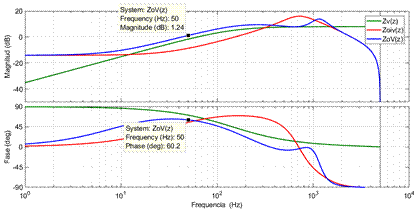
impedancia virtual sobre la impedancia de salida pueden observarse en la Fig. 7., donde se presenta la
impedancia de salida del sistema obtenida con los controladores de los lazos
internos de control de tensión y corriente Zoiv, y la
impedancia de salida con el agregado del lazo de impedancia virtual ZoV.
Es posible apreciar en la Fig. 7., la efectividad que tiene
el lazo de impedancia virtual para mantener una característica
predominantemente inductiva en la impedancia de salida, ya que la fase resultante
de ZoV está entre la de Zv y la de Zoiv,
siendo su valor 60,2°. En cuanto al valor de la magnitud de ZoV,
la misma resultó en 1,24 dB a 50 Hz, lo que equivale a 1,15 Ω a 50 Hz; y
por tanto, la magnitud de Zoiv es de -10dB, lo que
corresponde a 0,32 Ω.
Fig. 7.
Respuesta
en frecuencia de Zv, Zoiv y ZoV.
Es importante notar que, a
baja frecuencia, tanto Zoiv(z) como ZoV(z)
parten de un comportamiento resistivo. Esto se debe a que se introdujo un
pequeño corrimiento del polo del integrador en el lazo de control de tensión,
pasando de (z – 1) a (z – 0,98), lo cual evita un comportamiento
completamente inductivo en las frecuencias bajas. El motivo por el cual se
realiza esta modificación en el polo integrador, es que como se analiza en la
sección 4, un comportamiento totalmente inductivo en torno a las frecuencias
bajas establece una componente de corriente continua en la corriente del
inductor cuando se conectan los inversores en paralelo, lo cual puede causar
pérdidas adicionales en el núcleo magnético de este componente. Esto se debe a
que la temperatura de operación del inductor puede aumentar por efecto Joule
ante la presencia de la componente de continua, lo que afecta a las
características del núcleo magnético, disminuye la permeabilidad y por lo tanto
aumentan las pérdidas en el inductor.
3.3.Control por curva de caída
En los generadores síncronos, debido
a las inercias inherentes de estas máquinas, cuando la potencia que requieren
las cargas alimentadas se incrementa, la frecuencia se reduce, disminuyendo a
su vez el ángulo de potencia. Debido a este principio, los generadores
conectados en paralelo encuentran naturalmente un punto común de operación y
comparten la potencia requerida por las cargas conectadas al sistema eléctrico.
Los inversores utilizados como
interfaces electrónicas de potencia entre las fuentes primarias de energía y la
red eléctrica no incorporan inherentemente ningún tipo de inercia, pero es
posible que emulen este comportamiento mediante una variación de la frecuencia
y amplitud de la tensión de salida en función de los valores medios de las
potencias activa y reactiva locales. Por este motivo, mediante el control por
curva de caída es posible lograr el sincronismo y estabilidad en sistemas
compuestos por inversores en paralelo.
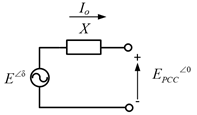
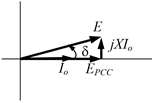
En la Fig. 8. se puede ver el circuito
equivalente de la tensión sintetizada por cada inversor, su impedancia de
interconexión con el punto común de conexión (PCC) y la tensión en este punto,
pudiéndose observar en la Fig. 9. un diagrama fasorial
donde se aprecia el ángulo δ entre la tensión sintetizada y la tensión del PCC.
Por simplicidad se representa a la
impedancia de interconexión como una reactancia, ya que ésta en realidad estará
dada por la impedancia de salida y la impedancia de los cables que separan al
inversor del PCC, existiendo siempre una porción resistiva.
Debe notarse que el control por curva
de caída introduce la capacidad de variación del ángulo de potencia del
inversor, añadiendo una realimentación negativa en el sistema que logra su
estabilidad mediante la selección del coeficiente m. Para las
simulaciones, cuyos resultados se muestran en la próxima sección, el
coeficiente m se escogió como 0,002, determinándose este directamente
por simulaciones numéricas. En cuanto al bloque de ganancia denominado como Kref,
este debe diseñarse para introducir una ganancia que escale a la señal de
referencia, de manera de obtener la tensión nominal en la condición de vacío.
Esto se debe a que, para la implementación del lazo de impedancia virtual, se
utiliza la corriente del inductor del filtro LC en lugar de la corriente
de salida io produciéndose una caída de tensión en la
condición de vacío a causa de iL, que debe ser compensada con
Kref.
Debido a que es posible reducir la
amplitud de la señal de tensión de referencia, ya sea mediante el lazo de
impedancia virtual como por la característica de caída lograda con Q, y que
mediante esto se consigue reducir la corriente de circulación entre los
inversores, es posible prescindir del droop sobre la potencia reactiva, por lo
que en este trabajo no se utiliza en las simulaciones. Por último, el esquema
presentado funciona correctamente solo en caso de que cada inversor tenga una
impedancia de salida predominantemente inductiva a frecuencia fundamental,
debiéndose realizar el control del ángulo a partir de la potencia reactiva si
la impedancia de salida fuese resistiva a dicha frecuencia [19].
4.
Resultados
de simulación
4.1.Paralelo de dos inversores
Para validar el funcionamiento en
paralelo de dos inversores con control por curva de caída y el diseño de los
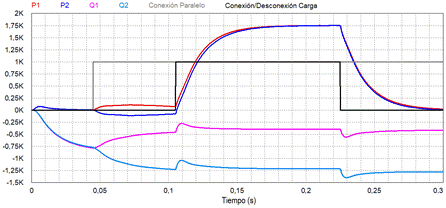
lazos internos de control e impedancia virtual, en la Fig. 10. se compara el cálculo de
potencias activa y reactiva media de ambos inversores, indicándose un primer
intervalo de tiempo donde comienzan a funcionar de manera independiente, luego
se produce la puesta en paralelo y finalmente, se realiza la conexión y
desconexión de una carga nominal por inversor.
En la Fig. 10. se observa la tendencia
de ambas potencias activas, las cuales tienden a igualarse una vez que se
conectaron en paralelo los inversores. Este comportamiento indica que se logró
el sincronismo entre los dos convertidores, observándose, además, que las
potencias activas se reparten equitativamente durante el resto del tiempo,
inclusive cuando ocurren los saltos de carga.
En cuanto a las potencias reactivas,
la diferencia observada se debe a la corriente de circulación que existe entre
los inversores, pudiéndose reducir su valor mediante el aumento de la magnitud
de la impedancia virtual.
Fig. 10.
Potencia
Activa (P) y Potencia Reactiva (Q) del inversor 1 y 2 funcionando
en paralelo.
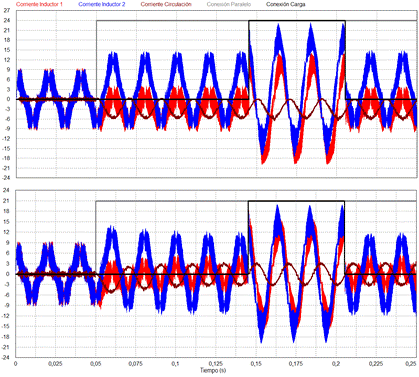
Para observar el comportamiento de la
corriente de circulación, en la Fig. 11. se presenta la misma
junto a las corrientes en los inductores, durante los tres eventos mostrados
anteriormente. En el gráfico superior, Fig. 11.(a), el controlador del
lazo de tensión corresponde al de la ecuación (1), lo cual produce un
comportamiento inductivo a baja frecuencia, observándose componentes de CC en
las corrientes de los inductores una vez realizada la conexión en paralelo. Si
bien esto no representa un efecto adverso para la carga a alimentar, ya que la
tensión provista se mantiene con un nivel de CC prácticamente nulo, la
componente de CC en los inductores causa pérdidas adicionales en estos
componentes, por lo que deben evitarse. En el gráfico que sigue de la Fig. 11.(b), se observa como este problema
es mitigado al introducir el polo del integrador dentro del círculo unitario,
utilizando la modificación de (z – 0,98) en lugar de (z – 1) en
la FT del controlador de tensión.
En la Fig. 11. (a) y (b) se puede
observar cómo, la magnitud de la corriente de circulación está vinculada
proporcionalmente a la diferencia entre las potencias reactivas entregadas por
cada inversor presentadas en la Fig. 10. Durante el funcionamiento
de los inversores en paralelo, la corriente de circulación toma un valor pico
de aproximadamente 3 A, lo que representa un 24% respecto del valor de corriente
nominal. Como se mencionó en la sección 3B, es posible disminuir esta corriente
de circulación aumentando la impedancia virtual, en detrimento de una menor
regulación de la tensión de salida. En trabajos futuros se analizarán las
pérdidas en cada inversor para poder definir un criterio para la selección del
valor de Zv.
Es importante mencionar que la
diferencia en el comportamiento de los inversores se debe únicamente a la
discrepancia en la ganancia de los sensores de tensión, ya que esta es la
diferencia paramétrica entre inversores que más afecta a la circulación de
corriente. Otro aspecto importante que destacar es que la corriente de
circulación es independiente de la carga como se observa en la Fig. 11.
Fig. 11.
De
arriba hacia abajo: Corrientes en los inductores de ambos inversores y
corriente de circulación entre inversores (a) para el caso en que se utiliza un
integrador puro en el controlador de tensión y (b) para el caso en que se
desplaza el polo del integrador hasta (z – 0,98).
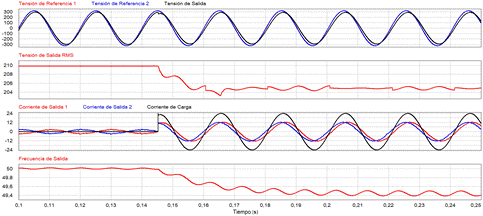
Para analizar el comportamiento de la
tensión de salida ante una entrada de carga con los dos inversores funcionando
en paralelo, en la Fig. 12.(a) se presenta el
resultado de simulación de la tensión sobre la carga y las señales de
referencia de cada inversor, observando que estas últimas se encuentran
superpuestas en todo momento, lo cual indicaría que los ángulos de estas dos
señales son iguales.
En la Fig. 12.(a), al momento de
conectarse la carga, se observa un pequeño transitorio en la tensión de salida,
por lo que se graficó en la Fig. 12.(b) el valor RMS de esta
tensión, visualizándose de mejor forma el efecto de la entrada de carga sobre
la tensión de salida. Luego de la entrada de carga es apenas perceptible el
corrimiento de los ángulos de las señales de referencias generadas por el
controlador por curva de caída, por lo que en la Fig. 12.(d) se graficó la
frecuencia de estas señales, la cual se midió sobre la frecuencia obtenida del
controlador droop del inversor 1.
Fig. 12.
De
arriba hacia abajo: (a) Señales de referencia de los lazos de control de
tensión y tensión sobre la carga, (b) RMS de la tensión sobre la carga, (c)
corrientes de salida de cada inversor y corriente sobre la carga y (d)
frecuencia del sistema.
Para el caso de alimentar cargas no
lineales, la estrategia propuesta debe modificarse para poder reducir la
impedancia de salida en un mayor rango de frecuencias. Esto puede hacerse
incluyendo algunos controladores resonantes en frecuencias específicas. El
agregado de estos controladores implica un aumento en el costo computacional,
pero será aún menor en comparación a las estrategias que utilizan solamente
controladores resonantes, debido a que el efecto de la acción integral actúa
sobre la frecuencia fundamental y las primeras armónicas de bajo orden. La
evaluación del número de resonantes a agregarse queda fuera de los alcances de
este trabajo.
4.2.Calidad de energía
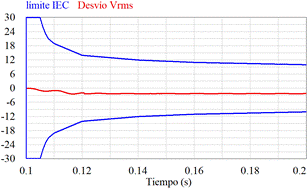
En la Fig. 13., se presenta el desvío
del valor RMS de la tensión de salida para dos inversores funcionando en
paralelo a los cuales se conecta una carga lineal, estando dentro de las cotas
establecidas por la clasificación más exigente de la norma IEC 62040-3, la cual
establece los límites de operación de la tensión provista a la carga para el
caso de fuentes ininterrumpidas de energía (UPS, Uninterruptible Power
Supplies). Se observa que en régimen permanente el desvío es de
aproximadamente 3%, existiendo un margen para incrementar la impedancia virtual
en caso de que se requiera disminuir la corriente de
circulación.
Fig. 13.
Desvío
del valor RMS de la tensión de salida respecto del valor nominal para una carga
lineal del 100%, y cotas establecidas por la clasificación 1 de la norma IEC
62040-3.
5.
Conclusiones
En este trabajo se propuso una
estrategia de control por curva de caída con lazo de impedancia virtual, que
logra un reducido costo computacional al implementar un controlador de amplio
ancho de banda. No se realizó un análisis cuantitativo del costo computacional
debido a que aún no fue implementado experimentalmente por el contexto actual
de pandemia de COVID-19. Para establecer los límites de la ganancia integral,
se propuso un análisis de la robustez del sistema ante variación paramétrica de
la inductancia del filtro LC, determinándose que el sistema con esta estrategia
de control es esencialmente robusto, tolerando una reducción del 68% del valor
de la inductancia respecto de su valor nominal. Además, se presentó el efecto
de la componente de corriente continua que aparece sobre las corrientes de los
inductores de los inversores en paralelo, una impedancia de salida con
característica inductiva a bajas frecuencias, junto con una propuesta para
mitigar este problema mediante la modificación de la acción integral del lazo
de control de tensión.
Los resultados de simulación presentados
validan la estrategia de control propuesta, observándose la relación de
compromiso existente entre corriente de circulación y regulación de tensión. Se
aprecia además el muy buen reparto de las potencias activas donde se puede ver
el funcionamiento sincrónico de los inversores en paralelo.
Se requieren realizar trabajos
futuros para establecer un criterio que permita seleccionar la magnitud de la
impedancia virtual, con el objetivo de establecer valores admisibles para la
corriente de circulación en función de las pérdidas de los convertidores.
Agradecimientos
Agradecemos al Ing.
Ricardo A. Korpys por sus observaciones y recomendaciones realizadas durante el
desarrollo de este trabajo en la cátedra de Proyecto y Diseño Electrónico. Este
trabajo fue financiado por el FONCyT a través del proyecto PICT 2017-3964
(UNaM), del CONICET a través del PIO 23720160100001CO y por la UNaM mediante
la financiación de proyectos especiales I16/I155 PI.
Referencias
[1] N.
Hatziargyriou, H. Asano, R. Iravani, and C. Marnay, "Microgrids," IEEE
Power and Energy Magazine, vol. 5, pp. 78-94, 2007.
[2] H. Han, X. Hou, J. Yang, J. Wu, M. Su, and J.
M. Guerrero, "Review of power sharing control strategies for islanding
operation of AC microgrids," Smart Grid, IEEE Transactions on, vol.
7, pp. 200-215, 2016.
[3] J. Rocabert, A. Luna, F. Blaabjerg, and P.
Rodríguez, "Control of power converters in AC microgrids," Power
Electronics, IEEE Transactions on, vol. 27, pp. 4734-4749, 2012.
[4] S. J. Chiang, C. Y. Yen, and K. T. Chang,
"A multimodule parallelable series-connected PWM voltage regulator," Industrial
Electronics, IEEE Transactions on, vol. 48, pp. 506-516, 2001.
[5] Z. Xiaotian and J. W. Spencer, "Linear
Voltage-Control Scheme With Duty-Ratio Feedforward for Digitally Controlled
Parallel Inverters," Power Electronics, IEEE Transactions on, vol.
26, pp. 3642-3652, 2011.
[6] B. A. Francis and W. M. Wonham, "The
internal model principle for linear multivariable regulators," Applied
Mathematics & Optimization, vol. 2, pp. 170-194, 1975.
[7] R. E. Carballo, F. Botterón, G. G. Oggier, and
G. O. García, "Design approach of discrete-time resonant controllers for
uninterruptible power supply applications through frequency response
analysis," IET Power Electronics, vol. 9, pp. 2871-2879, 2016.
[8] D. N. Zmood, D. G. Holmes, and G. H. Bode,
"Frequency-domain analysis of three-phase linear current regulators,"
Industry Applications, IEEE Transactions on, vol. 37, pp. 601-610, 2001.
[9] M. Tomizuka, T.-C. Tsao, and K.-K. Chew,
"Discrete-Time Domain Analysis and Synthesis of Repetitive
Controllers," in American Control Conference, 1988, 1988, pp.
860-866.
[10] T.-F. Wu, C.-H. Chang, L.-C. Lin, G.-R. Yu, and
Y.-R. Chang, "A D-Σ
Digital Control for Three-Phase Inverter to Achieve Active and Reactive Power
Injection," IEEE Transactions on Industrial Electronics, vol. 61,
pp. 3879-3890, 2013.
[11] X. Wang, Y. Li, F. Blaabjerg, and P. C. Loh,
"Virtual-Impedance-Based Control for Voltage-Source and Current-Source
Converters," 2015.
[12] J. M. Guerrero, L. Garcia de Vicuna, J. Matas,
M. Castilla, and J. Miret, "Output Impedance Design of Parallel-Connected
UPS Inverters With Wireless Load-Sharing Control," Industrial
Electronics, IEEE Transactions on, vol. 52, pp. 1126-1135, 2005.
[13] R. E. Carballo, "Estrategias de control
para la conexión en paralelo de inversores en UPS," Tesis doctoral,
Facultad de Ingeniería, Universidad Nacional de Río Cuarto, Río Cuarto, 2017.
[14] P. Mattavelli, F. Paolo, F. Dal Lago, and S.
Saggini, "Analysis of Control-Delay Reduction for the Improvement of UPS
Voltage-Loop Bandwidth," Industrial Electronics, IEEE Transactions on, vol.
55, pp. 2903-2911, 2008.
[15] T. B. Lazzarin, G. A. T. Bauer, and I. Barbi,
"A Control Strategy for Parallel Operation of Single-Phase Voltage Source
Inverters: Analysis, Design and Experimental Results," Industrial
Electronics, IEEE Transactions on, vol. 60, pp. 2194-2204, 2013.
[16] R. E. Carballo, F. Botterón, G. G. Oggier, and
G. O. García, "Estrategia de Control Droop con Reducido Número de Sensores
Para Inversores en UPS," presented at the IEEE ARGENCON 2016, Buenos
Aires, 2016,
http://www.edutecne.utn.edu.ar/argencon2016/trabajos/IEEE_ARGENCON_2016_paper_295.pdf.
[17] Y. Wei, C. Min, J. Matas, J. M. Guerrero, and
Q. Zhao-ming, "Design and Analysis of the Droop Control Method for
Parallel Inverters Considering the Impact of the Complex Impedance on the Power
Sharing," Industrial Electronics, IEEE Transactions on, vol. 58,
pp. 576-588, 2011.
[18] J. M. Guerrero, J. Matas, L. G. de Vicuña, M.
Castilla, and J. Miret, "Wireless-Control Strategy for Parallel Operation
of Distributed-Generation Inverters," Industrial Electronics, IEEE
Transactions on, vol. 53, pp. 1461-1470, 2006.
[19] J. M. Guerrero, J. Matas, L. G. de Vicuña , M.
Castilla, and J. Miret, "Decentralized Control for Parallel Operation of
Distributed Generation Inverters Using Resistive Output Impedance," Industrial
Electronics, IEEE Transactions on, vol. 54, pp. 994-1004, 2007.
[20] R. E. Carballo, F. Botterón, G. G. Oggier, and
G. O. García, "Droop control with capacitive virtual impedance loop for
single-phase parallel inverter systems," in 2018 IEEE Biennial Congress
of Argentina (ARGENCON), 2018, pp. 1-6.
[21] P. Kundur, N. J. Balu, and M. G. Lauby, Power
system stability and control vol. 7: McGraw-hill New York, 1994.
[22] E. A. A. Coelho, P. C. Cortizo, and P. F. D.
Garcia, "Small-signal stability for parallel-connected inverters in
stand-alone AC supply systems," Industry Applications, IEEE
Transactions on, vol. 38, pp. 533-542, 2002.