Vol. 2 N° 2,
julio-diciembre 2020, pag. 37-45
ISSN 2618-5520 on
line
DOI - https://doi.org/10.36995/j.masingenio.2021.02.02.003
Modelación matemática de procesos en la industria química y fermentativa
Pérez Navarro O.a *, González Suárez E.a, Rodríguez Rico I.a, Miño Valdés J.E.b
a Universidad Central de las Villas (UCLV), Facultad de Química y Farmacia, Santa Clara, Cuba
b Universidad Nacional de Misiones (UNaM), Facultad de Ingeniería, Oberá, Argentina
opnavarro@uclv.cu, erenio@uclv.edu.ar, ivanl@uclv.edu.cu, minio@fio.unam.edu.ar
Resumen
Para efectuar la modelación de un reactor es necesario obtener el mayor conocimiento de las propiedades termodinámicas, físicas y químicas del sistema, la cinética de las reacciones, las características térmicas y otras específicas. El objetivo de este trabajo fue abordar metodológicamente la modelación de procesos químicos y biológicos, para estudiar etapas con reacciones químicas mediante modelos matemáticos. Se han presentado métodos analítico-matemáticos para el análisis cinético y el tratamiento estadístico de datos experimentales de la industria. Varias situaciones reales han sido resueltas aplicando los modelos globales presentados. Se expresó el tratamiento estadístico de datos industriales para complementar modelos con reacciones químicas. Se presentó un diagrama heurístico diseñado para la modelación de un reactor químico o fermentativo.
Palabras Clave – Industria química y fermentativa, Modelación matemática, Procesos.
.
Abstract
To carry out the modeling of a reactor, it is necessary to obtain the greatest knowledge of the thermodynamic, physical and chemical properties of the system, the kinetics of the reactions, the thermal characteristics and other specific. The objective of this work was to methodologically approach the modeling of chemical and biological processes, to study stages with chemical reactions using mathematical models. Analytical-mathematical methods have been presented for the kinetic analysis and statistical treatment of experimental data from the industry. Several real situations have been resolved by applying the global models presented. Statistical treatment of industrial data was expressed to complement models with chemical reactions. A heuristic diagram designed for the modeling of a chemical or fermentative reactor was presented.
Keywords – Chemical and fermentative industry, Mathematical modeling, Processes.
1. Introducción
Desde finales del siglo pasado se ha logrado un avance importante en la consideración matemática y fenomenológica asociada a la investigación en el campo de la ingeniería química. Sin embargo, es significativo que todavía muchos de los trabajos reportados, incluso al máximo nivel, tratan a los reactores químicos y biológicos dentro de una etapa, sin considerar sus interioridades como equipo, entre otras cosas, por su complejidad. Sin duda alguna, la modelación de reactores, donde se producen simultáneamente fenómenos de transferencia de masa y de calor, junto con reacciones químicas, exige que el investigador tenga que estudiar meticulosamente muchos factores y decidir cuáles son los de mayor influencia. En ocasiones estas decisiones permiten simplificar los modelos, pero en muchos casos, no es posible lograr reducciones importantes en su complejidad matemática.
El objetivo de este trabajo fue abordar metodológicamente la modelación de reactores químicos y biológicos, para estudiar etapas con reacciones químicas mediante modelos matemáticos.
2. Materiales y Métodos
2.1. Modelación de reactores químicos
Se han presentado métodos analítico-matemáticos para el análisis cinético y se expresa el tratamiento estadístico de los datos experimentales industriales con el objetivo de brindar posibilidades para complementar los modelos que se han realizado o se planean realizar.
Para el análisis cinético se expresa el tratamiento estadístico de los datos experimentales industriales con el objetivo de brindar posibilidades para complementar los modelos que se han realizado o se planean realizar sobre etapas con reacción química.
Para efectuar la modelación de un reactor es necesario lograr el mayor conocimiento de la siguiente información [1] [2] [3]:
o Propiedades termodinámicas, físicas y químicas del sistema reaccionante.
o Cinética de las reacciones participantes.
o Características térmicas del sistema.
o Características específicas y generales del catalizador para las reacciones catalizadas heterogéneas.
En la medida en que se tenga más dominio de esta información serán más precisos los modelos que se pueden evaluar. Si se tiene completa información sobre los aspectos señalados, se pueden obtener modelos muy robustos, capaces de permitir:
· Analizar la influencia de cada variable en el funcionamiento del reactor.
· Analizar posibles anomalías del sistema originadas por cambios en la alimentación o alteraciones en las condiciones de operación de otros equipos que inciden sobre la operación del reactor.
· Simular, optimizar y controlarlos parámetros de operación del equiposobre la base de un criterio técnico y económico.
· Evaluar posibles sustitutos.
Por otra parte, si solo se conocen parcialmente los aspectos necesarios, los modelos tendrán limitaciones en su comprobación y uso, de cuya extensión dependerá la efectividad del análisis del proceso.
Los modelos matemáticos que representan el comportamiento de un reactor químico son agrupados de la forma siguiente [4] [5]:
1. Modelos fenomenológicos, basados en los fenómenos físicos y químicos, expresados a través de la termodinámica, la cinéticay los balances de masa y energía.
2. Modelos basados en correlaciones experimentales entre las variables, que se deducen y comprueban aplicando procedimientos estadísticos.
En los modelos correspondientes al primer grupo se destacan los cinéticos. En ellos, la velocidad depende de múltiples factores y por lo general es conveniente considerar como los de mayor impacto las concentraciones y la temperatura. Sin embargo, dependiendo del proceso, es común que sea necesario considerar la influencia del pH, los procesos difusionales, la transferencia de calor y otros. Por estas razones, en muchas ocasiones se prefieren usar modelos asociados al segundo grupo. El estudio de la hidrólisis del bagazo con ácido sulfúrico concentrado para la obtención de etanol, reportado por Boutros Sarrouh [6] ilustra con efectividad esta situación, donde los modelos estadísticos son usados para establecer adecuadamente los parámetros de trabajo del reactor, sin llegar a la evaluación fenomenológica.
Pero lo más común es la combinación de ambos métodos pues los efectos micro cinéticos, sobre cualquier sistema, son específicos de su naturaleza y los modelos desarrollados pueden adaptarse con precisión al tratamiento de datos prácticos, adquiridos a través de diseños experimentales efectivos.
En sistemas homogéneos la cinética es expresada solamentea través de la etapa química, siendo el volumen del sistema el factor determinante en el diseño y evaluación. Sin embargo, en sistemas heterogéneos esta etapa se combina con las difusionales, siendo necesario considerar la influencia relativa de todas las etapas presentes y adquiriendo un significado determinante la búsqueda de la etapa controlante del proceso. De dicha etapa depende la definición del modelo de contacto ponderando los requerimientos de volumen del equipo o de área de contacto dependiendo del predominio de las etapas qcas. o las difusionales [1] [2] [3].
Los balances de materiales y energía dependen del modelo de contacto requerido en el equipo. Para Reactores Continuos con Agitación (RCCA) en los que puede considerarse estado estacionario y mezclado perfecto o con escasas desviaciones del mismo, los balances resultan en ecuaciones ordinarias. Sin embargo, para equipos discontinuos, que por sus características operacionales funcionan en estado no estacionario, los balances resultan en ecuaciones diferenciales totales respecto al tiempo de reacción [2].
Situación parecida se presenta para reactores tubulares continuos con modelo de flujo en pistón (RCFP) o de escasa dispersión, que operan en estado estacionario, sin embargo en dicho equipo, cambian de las propiedades con la posición. En este último caso los modelos de los balances resultan en ecuaciones diferenciales totales respecto a la posición. En ellos la posición puede serexpresada como la concentración o la conversión [1] [2].
En la mayoría de los trabajos que desarrollan la modelación de reactores químicos y biológicos se combinan modelos fenomenológicos y métodos estadísticos. Varias situaciones reales han sido resueltas aplicando los modelos globales que a continuación se describen:
1. Modelo homogéneo (ideal) para reactores isotérmicos y adiabáticos:
Para RCCA la solución es directa, para reactores discontinuos o RCFP, los balances se resuelven por integración en el caso isotérmico. Sin embargo, en el caso adiabático y en el no isotérmico-no adiabático se necesita un método numérico iterativo [1].
2. Modelo pseudo-homogéneo con dispersión en una coordenada para operación adiabática y no isotérmica-no adiabática.
En este modelo se tiene en cuenta la variación de la difusividad de masa y la conductividad térmica efectiva solo en la dirección axial. Su solución también se logra por un método numérico [1]. El procedimiento que se aplica en los casos 1 y 2 también se conoce como método simplificado.
3. Modelo pseudo-homogéneo con dispersión de dos dimensiones para operación adiabática y no isotérmica no adiabática.
En este caso se considera la variación de la difusividad efectiva de masa y la conductividad térmica en la dirección axial y radial. Es muy importante elegir adecuadamente las condiciones de contorno para la solución del sistema de ecuaciones diferenciales parciales.
Generalmente se considera que, en las secciones de entrada y salida del reactor, los gradientes son cero [1]. Este procedimiento también se conoce como método semi-riguroso cuando puede asumirse que no existe variación de las propiedades físicas del sistema con la temperatura.
4. Modelo heterogéneo bidimensional:
Este modelo recoge todas las diferencias posibles entre la fase sólida y el fluido reaccionante, sobre todo las diferencias de temperatura. En muchos casos la fase sólida es el catalizador presente en la reacción. Para lograr una solución adecuada del sistema de ecuaciones diferenciales se necesita la más amplia información sobre el sistema reaccionante.
Su solución se obtiene aplicando métodos numéricos [1]. Este procedimiento también se conoce como método riguroso, es el de solución más compleja pero más exacta e incluye al resto de los modelos, siendo sus expresiones generales del balance de masa y energía dadas en las ecuaciones siguientes:
|
|
(Ec.1) |
|
|
(Ec.2) |
En ellas, se manifiesta el balance de masa (Ecuación1) y el balance de energía (Ecuación2) para un sistema reaccionante con variación de la concentración y la temperatura (y por consiguiente la velocidad de reacción) en la posición radial y longitudinal combinada con la variación de las propiedades físicas en ambas direcciones. En el caso de sistemas heterogéneos en los que están presentes sólidos estas propiedades se refieren a la difusión y conducción térmica en el sólido hipotético [1].
3. Resultados
3.1. Obtención de los modelos cinéticos a través de procedimientos experimentales y estadísticos
El procedimiento por métodos estadísticos no ha estado totalmente sistematizado, ya que el planteamiento del modelo depende totalmente de las variables a considerar, de sus interdependencias, de las posibilidades de obtención de datos experimentales en condiciones que permitan explorar las variables en sus rangos de trabajo y del conocimiento previo que se tenga del sistema en estudio.
A partir de diseños de experimentos factoriales completos o fraccionadosse pueden evaluar modelos estadísticos en los pueden o no considerarse todas las interacciones de primer y segundo orden. La experiencia ha demostradoque es muy poco probable que las interacciones de tercer orden sean significativas.
La selección del modelo exige que mediante los procedimientos de la regresión lineal múltiple sean evaluados los coeficientes usando datos de operación normales que presenten variación de las variables en sus rangos o con datos de experimentos planeados al efecto y realizar el análisis de varianza para discriminar los términos del modelo que no tienen influencia significativa sobre la respuesta. Una limitación importante en la evaluación de estos modelos es el gran número de corridas que es necesario hacer para obtener buenos resultados. Sin embargo, los diseños factoriales fraccionados y otros diseños más robustos como el de [8] permiten disminuir el número de corridas experimentales.
Cuando existen dependencias no lineales entre las variables se pueden proponer modelos que contienen términos no lineales y cuadráticos en los que se plantean exponentes que son evaluados junto a los coeficientes. En estas situaciones se linealizan los términos de los modelos y seevalúan los mismos por el método de regresión no lineal múltiple. A este grupo pertenecen algunos de los trabajos reportados [9].
3.2. Procedimientos experimentales y analíticos
Dependiendo de la complejidad de las ecuaciones resultantes del balance de materiales en el reactor y del tipo de modelo de contacto seleccionado para lasexperiencias cinéticas, es conveniente usar el método de análisis integral o el diferencial. Para reacciones homogéneas es conveniente efectuar dichas experiencias en equipos discontinuos, sin embargo para procesos catalíticos heterogéneosse necesitan reactores integrales o diferenciales [1] [2].
Las investigaciones encaminadas al conocimiento de la cinética de las reacciones presentan en muchos casos un alto grado de complejidad en lo referente a recursos materiales y técnicas analíticas, lo que en ocasiones justifica que se planteen simplificaciones que faciliten el análisis cinético. Entre ellas se encuentra la búsqueda del semiperíodo dereacción y el trabajo en aislamiento a causa del exceso de un reactante [3].
Por otra parte, es muy importante la investigación del mecanismo para reacciones complejas. Ello requiere el análisis de los posibles mecanismos de reacción y el diseño experimental y analítico detallado que permita dar solución a dicha problemática. Para ello también es imprescindible establecer el análisis de distribución de producto, las condiciones de operacióny el modelo de contacto adecuado para lograr dicha distribución. A estos aspectos brindan un tratamiento adecuado los trabajosde Pérez y colaboradores [10] [11] [12] [9], referidos a la cinética y distribución de producto en la acetilación básica acuosa de almidón de Manihot esculenta Crantz.
Dichos trabajos ilustran además como la adecuada selección de los parámetros de operación del proceso permite que una reacción compleja pueda ser considerada como una reacción simple en determinadas condiciones.
3.3. Procedimientos experimentales combinados con simulación de modelos teóricos
La simulación del comportamiento de modelos teóricos previamente desarrollados y la obtención de sus parámetros para describir el comportamiento experimental es una vía interesante de modelación cinética que es muy usada en biorreactores. Ello puede efectuarse ajustando la diferencia entre los modelos, teórica y experimental, a través del método de los mínimos cuadrados, pruebas de hipótesis de significación del modelo o la mínima integral del error de la sumatoria de las diferencias entre ellos. A esta última situación da una solución adecuada un trabajo de Pérez y colaboradores [13] [14], referido a la modelación de la cinética de obtención de biomasa proteica.
Una opción interesante que pertenece a este grupo,es la brindada por Albernas [15] [16], referida a la obtención del modelo cinético pseudo-homogéneo de Michaelis-Menten para la producción de azúcares reductores totales en la hidrólisis enzimática del bagazo.
3.4. Diagrama heurístico para la modelación de un reactor químico o fermentativo
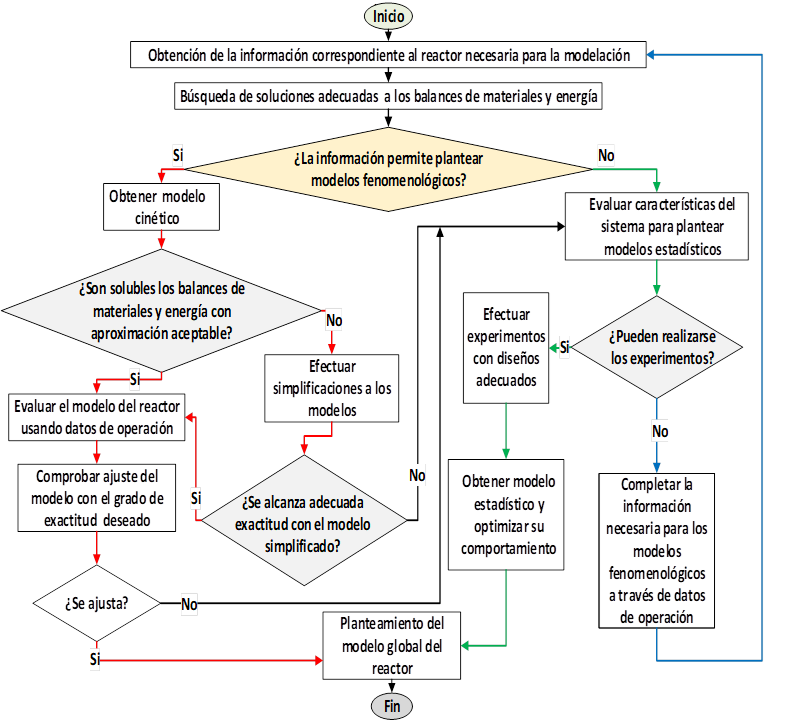
Atendiendo a los análisis anteriores, es posible plantear una metodología general aplicable a cualquier situación específica a modo de modelo heurístico, capaz de considerar las particularidades de un sistema y tomar decisiones quepermitan evaluar con buena precisión su modelo. Dicho diagrama se muestra en la Figura 3. En esta figura las líneas rojas corresponden a acciones de modelación fenomenológica, lasverdes al método estadístico y las azules a acciones de modelación combinada
|
|
Fig.3. Diagrama heurístico para la modelación de un reactor químico o fermentativo
Fuente: elaboración propia, 2019
Dicho diagrama brinda un tratamiento lógico a la tarea de modelación y sigue los principios anteriormente referidos. En el mismo, luego de disponer de la información necesaria para la modelación y de la precisión de las condiciones del contacto, las posibles expresiones de caracterización y el carácter térmico de los procesos presentes, se define si es posible el planteamiento de modelos fenomenológicos. En caso afirmativo se efectúa la modelación cinética yse resuelven los balances de materiales y energía, cuya expresión más general es dada en las ecuaciones (1) y (2), a partir de las condiciones que garanticen una aproximación aceptable. Si ello es posible, se evalúa y comprueba el ajuste del modeloa datos de operación. De lograr ajuste se plantea el modelo como expresión global del reactor.
Si la aproximación alcanzada no es aceptable, se efectúan simplificaciones y se evalúa el modelo simplificado. Si el modelo simplificado no es adecuado o si el ajuste del modelo fenomenológico a los datos de operación no alcanza la exactitud necesaria, se abandona la vía fenomenológica y se procede al análisis para evaluar modelos estadísticos. Esta última opción también es considerada cuando no es posible el planteamiento de modelos fenomenológicos.
Al evaluar si las características del sistema permiten aplicar modelos estadísticos puede existir la posibilidad de efectuar experimentos previamente diseñados con la finalidad de obtener el modelo estadístico y aplicar el método de optimización más adecuado al caso. El modelo estadístico en sus condiciones óptimas constituye el modelo global del reactor.Cuando no pueden aplicarse experimentos previamente diseñados se completa la información necesaria para la modelación fenomenológica a través de datos de operación. El procedimiento concluye con el planteamiento de la expresión global del reactor.
4. Conclusiones
Los estudios para la caracterización de reactores, realizados a escala de laboratorio permiten modelar su cinética como paso básico en la obtención del modelo global del reactor.
Dichas pruebas y las efectuadas en equipos pilotos, se pueden plantear como experimentos a escala de planta que bien meditados logran la máxima eficiencia en la investigación.
La modelación de reactores químicos a escala industrial tiene en general tres aspectos a considerar con la mayor profundidad:
· Las características experimentales que se tienen en la industria elegida y la información disponible.
· Los modelos matemáticos posibles a evaluar.
· Los procedimientos estadísticos y matemáticos que permiten el análisis del ajuste de cada modelo.
El objetivo central que rige el trabajo de modelación de un reactor es determinar las condiciones óptimas (o región óptima de operación) de los reactores químicos sin profundizar totalmente en el mecanismo o cinética de las reacciones que en ellos se producen, pero a la vez sin desatenderlas. Esto se puede asegurar en gran medida con la adecuada selección del modelo, conjugando aspectos cinéticos y estadísticos.
Referencias
[1] Smith, J. M. 1991. Chemical Engineering Kinetics. Mc. Graw Hill Book Company.
[2] Levenspiel, O. 1999. Chemical Reaction Engineering, New York, USA, Willey Press.
[3] Fogler, H. 2001. Elementos de Ingeniería de las Reacciones Químicas. 3a ed., México, Pearson Educación.
[4] Perry, R. & Green, D. 1984. Perry's chemical Engeerieng handbook. Mc Graw-Hill Book Company.
[5] Montgomery, D. C. 2004. Diseno y análisis de experiementos, Limusa Wiley. 2ª ed. .
[6] Coulson, J. M., Richardson, J. F. & Sinnott, R. K. 2005. Chemical Engeneering Design, Elseiver Butterworth-Heinemann. 4a ed. Vol 6.
[7] Boutros Sarrouh, F., Jover, J. & González, E. 2005. Estudio de la hidrólisis del bagazo con ácido sulfúrico concentrado utilizando dos variantes en una sola etapa y una sola etapa modificada para la obtención de etanol y análisis técnico económico de dicho proceso. Revista Ingeniería e Investigación, 25 (3), 34-38.
[8] González, E. 1991. Utilización del análisis de procesos en la intensificación de la producción en distintas industrias de Cuba” Tesisen Opción al Grado Científico de Doctor en Ciencias, Universidad Central Marta Abreu de Las Villas.
[9] Miño, J. E., González, E. & Pérez, O. (eds.) 2019. Contribución de la ingeniería de las reacciones químicas al desarrollo de nuevos procesos industriales: Dacultad de ingeniería, Universidad Nacional de Misiones. Argentina.
[10] Pérez, O., Ley, N., Gonzáles, E. & Toledo, L. 2018a. Cinética y Distribución de Producto en la Acetilación de Almidón de bajo Grado de Sustitución a partir de Manihot esculenta Crantz, variedad INIVIT Y-93-4. Centro Azúcar, 45, 88-100.
[11] Pérez, O., Ley, N., González, E. & Toledo, L. C. 2018b. Cinética y Distribución de Producto en la Acetilación de Almidón de bajo Grado de Sustitución. Afinidad, LXXV, 204-211.
[12] Pérez, O. 2018. Procedimiento estratégico de desarrollo de procesos agroindustriales complementado con asimilación tecnológica aplicado a los productos de Manihot esculenta Crantz. Tesis en opción al Grado Científico de Doctor en Ciencias Técnicas, Universidad Central "Marta Abreu" de Las Villas.
[13] Pérez, O., Miño, J. E., García, A. & González, E. 2019a. Fermentative Kinetic Modelling forProtein Biomass from Sugar Diversification. Current Trends in biomedical Engeneering and Biosciences.Junipers Publishers, CTBEB. MS.ID.555998.
[14] Pérez, O., Miño, J. E., García, A. & González, E. 2019b. Modelación de la cinética fermentativa en la obtención de biomasa proteica a partir de la diversificación azucarera. In: MIÑO, J. E., GONZÁLEZ, E. & PÉREZ, O. (eds.) Contribucióin de la Ingeniería de las reacciones químicas al desarrollo de nuevos procesos industriales. . Facultad de Ingeniería. Universidad Nacional de Misiones. Argentina. Primera edición.
[15] Albernas, Y., Corsano, G., Mesa, L., Santos, R. & González, E. 2015 Estudio de la cinética de la hidrolisis enzimática del bagazo pretratado. AFINIDAD, LXXII.
[16] Albernas, Y., Pedraza, J., Corsano, G., Mesa, L., Rodríguez, I. L. & González, E. 2016. Primera aproximación a la cinética de obtención d eetanol mediante sacarificación y fermentación simultanea debagazo. AFINIDAD LXXIII 191-196.