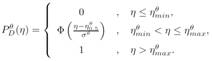Vol. 2 N°2,
julio-diciembre 2020, pag. 46-58
ISSN 2618-5520 on
line
DOI - https://doi.org/10.36995/j.masingenio.2021.02.02.004
Estrategias para la Inspección Óptima de Estructuras de Hormigón Armado Sujetas a Corrosión
Benítez P.a,b,*, Rocha E.c, Rodrigues F.b
a Universidad Nacional de Itapúa (UNI), Facultad de Ingeniería, Encarnación, Itapúa, Paraguay.
b Universidad de Aveiro, Departamento de Ingeniería Civil, RISCO, Aveiro, Portugal.
c Universidad de Aveiro, Departamento de Matemáticas, CIDMA, Aveiro, Portugal.
pablo.benitez@fiuni.edu.py, mfrodrigues@ua.pt, eugenio@ua.pt
Resumen
Gran parte de las estructuras de hormigón armado se han construido en la primera mitad del Siglo XX, por lo que su vida útil se encuentra actualmente en una etapa crítica desde la perspectiva del mantenimiento. Uno de los mecanismos de degradación más frecuentes y costosos en este tipo de infraestructura está asociado con la corrosión del refuerzo inducida por el fenómeno de carbonatación. Bajo este contexto, el objetivo de este artículo fue la formulación de un modelo de toma de decisiones para la planificación de la inspección óptima. Los tiempos de inspección fueron optimizados considerando la incertidumbre inherente al proceso de degradación y una compensación entre los costos de inspección y la capacidad de servicio de la estructura. Se ha elaborado un análisis de eficiencia a través de dos enfoques: el Análisis de Frontera Estocástica y el Análisis de Envolvente Multidireccional. Este análisis proporciona una evaluación que reduce el número de técnicas de inspección necesarias y el intervalo de tiempo entre inspecciones para proporcionar no solo una solución óptima, sino también más eficiente. Así, el resultado de esta investigación comprende un modelo numérico para la obtención de los tiempos de inspección más adecuados durante la vida útil de la estructura.
Palabras Clave – Análisis de Eficiencia, Carbonatación, Corrosión, Durabilidad, Hormigón armado, Inspección,
Mantenimiento, Modelo de decisión, Optimización.
.
Abstract
Much of the reinforced concrete structures were built in the first half of the 20th century, so their service life is currently at a critical stage from a maintenance perspective. One of the mechanisms more frequent and costly degradation in this type of infrastructure is associated with reinforcement corrosion induced by the phenomenon of carbonation. In this context, the objective of this article was the formulation of a Decision-making model for optimal inspection planning. The inspection times were optimized considering the uncertainty inherent in the degradation process and a trade-off between the costs of inspection and serviceability of the structure. An efficiency analysis has been developed through two approaches: Stochastic Frontier Analysis and Multidirectional Envelope Analysis. This analysis provides an assessment that reduces the number of inspection techniques required and the time interval between inspections to provide not only an optimal solution, but also a more efficient one. Thus, the result of this research It comprises a numerical model to obtain the most adequate inspection times during the useful life of the structure.
Keywords – Efficiency Analysis, Carbonation, Corrosion, Durability, Reinforced Concrete, Inspection, Maintenance,
Decision Model, Optimization.
1. Introducción
El estudio del desempeño y durabilidad de las estructuras de hormigón armado comprende un punto importante de la investigación científica en el campo de la ingeniería civil, el cual en las últimas décadas se ha desarrollado y ha evolucionado constantemente [1-4]. El hormigón armado es uno de los materiales más utilizados a nivel mundial en estructuras e infraestructuras debido a su versatilidad y un costo de producción relativamente bajo. Sin embargo, al igual que cualquier otro material constructivo, el hormigón tiende a degradarse con el paso del tiempo, afectando así a su vida útil. Por esta razón, establecer estrategias de mantenimiento comprende una tarea fundamental para preservar la durabilidad de este tipo de infraestructuras.
La corrosión del refuerzo en las estructuras de hormigón armado causa la fisuración, desprendimiento del recubrimiento y pérdida de su adherencia en el material, siendo así uno de los mecanismos de degradación más comunes y costosos en este tipo de estructuras. Además, la fisuración y el desprendimiento también puede facilitar el acceso de agentes perjudiciales para el concreto y las barras de refuerzo [5]. De esta manera, la corrosión en el hormigón armado puede ser causado mediante dos fenómenos: el ataque de cloruros y la carbonatación. La carbonatación del hormigón es un mecanismo de degradación frecuente en regiones tropicales con climas húmedos y altas temperaturas [6]. Por lo tanto, esta investigación está enfocada a la corrosión inducida por la carbonatación del hormigón, el cuál es un fenómeno típico que se presenta en las estructuras de Paraguay y otros países del continente.
La detección temprana de los problemas de corrosión en estructuras de hormigón armado supone un considerable ahorro en los costos de mantenimiento de la misma. Sin embargo, el mantenimiento afecta directamente a la fiabilidad estructural de los componentes, es decir, un mantenimiento muy reducido compromete a un pobre desempeño estructural y a fallas costosas en el sistema constructivo y la fiabilidad se degrada. Por otro lado, si se realiza un mantenimiento muy frecuente, la fiabilidad mejora, sin embargo, el costo de mantenimiento se incrementa drásticamente [7].
De esta manera, es necesario el desarrollo de un marco sistemático para la toma de decisiones que sirva como una herramienta para el planeamiento óptimo de las inspecciones. Así pues, esta herramienta debe considerar un conjunto de métodos de intervención y abordar un gran número de objetivos asociados con el problema de optimización bajo el enfoque de la eficiencia [8]. No obstante, la elección de una determinada técnica de inspección, así como el momento al cual se realizará dicha intervención, afectará los resultados de la toma de decisiones tanto técnica como económicamente [9].
Esta investigación considera la gestión de las estrategias de mantenimiento como un problema de optimización que está orientada a minimizar el costo asociado con el planeamiento de inspecciones. Además, el estudio también busca mantener un mínimo nivel de fiabilidad estructural a través de un análisis de probabilidad de falla en la estructura. Para el análisis se han tenido en cuenta parámetros como el costo de cada técnica de inspección, el costo total del planeamiento de la inspección, el recubrimiento de la estructura, la tasa de corrosión y la resistencia característica de la estructura. Por consiguiente, debido a la naturaleza estocástica del análisis, el estudio presentado está basado en un enfoque probabilístico.
Por último, un análisis de eficiencia se desarrolló como complemento del análisis de optimización multi-objetivo. Este análisis permite identificar cual es la mejor estrategia de entre un conjunto de soluciones optimas que satisfagan varios criterios simultáneamente. Los métodos de eficiencia aplicados para verificar su aplicabilidad en el planeamiento de inspecciones fueron el Análisis de Frontera Estocástica (SFA) y el Análisis de Envolvente Multidireccional (MEA). Este análisis de eficiencia es aplicado considerando dos aspectos principales: la variedad de técnicas de inspección necesarias en el planeamiento, y el periodo de tiempo total del planeamiento de inspecciones, es decir, el periodo de tiempo entre la primera y la última inspección.
Estos parámetros considerados en el análisis de eficiencia son muy significativos ya que como resultado se obtiene la estrategia de inspección que requiere la menor cantidad de recursos (técnicas y equipos de inspección) y la menor cantidad posible de tiempo de trabajo para alcanzar el mismo o mejores resultados que los resultados obtenidos únicamente con un análisis de optimización. En resumen, esta investigación tiene como objetivo principal desarrollar un modelo numérico para determinar los tiempos de inspección en estructuras de hormigón armado sujetas a degradación por corrosión. La aplicación de este modelo permite conocer el momento óptimo para la inspección en la estructura y cuál es la técnica de inspección más adecuada a ser aplicada considerando la eficiencia de la inspección.
1.1. Análisis de Eficiencia
El análisis de eficiencia está basado en cuatro elementos: las unidades de toma de decisión, datos de entrada, datos de salida, y la función de producción [10]. De este modo, en el análisis de eficiencia se estudia la variación de datos de entrada que genera un mismo valor de salida considerando una función de producción (también definido como función de frontera) que describe la transformación de los datos de entrada en datos de salida. Si la solución óptima está dentro de la frontera, entonces se establece que dicha solución es técnicamente eficiente [11].
Existen dos métodos comúnmente usados en este tipo de análisis. Por un lado, el MEA usa métodos de programación matemática desde un enfoque no paramétrico para identificar los mayores niveles de salida mediante la combinación de diferentes datos de entrada. Por otro lado, el SFA aplica métodos econométricos desde un enfoque paramétrico para identificar los niveles de producción más elevados [12]. El método SFA es probablemente el método mas común para este tipo de estudios [13], aunque el MEA tiene la ventaja de poder analizar múltiples datos de entrada/salida que podría ser más apropiado para la modelación de la estrategia de toma de decisiones en el planeamiento de inspecciones, donde varios criterios son considerados generalmente.
A pesar de que las técnicas de análisis de eficiencia han sido ampliamente desarrolladas en otras áreas de la ciencia, en la industria de la construcción ha recibido menos atención que en bibliografías referidas, por ejemplo, a la economía, energía, agricultura, entre otros [14]. En este estudio, este análisis de eficiencia busca formular un plan de inspecciones que permita el menor uso de recursos en un menor periodo de tiempo asegurando una fiabilidad mínima en la estructura.
2. Metodología
La formulación matemática para el planeamiento optimizado de las inspecciones es presentada en esta sección, la cual está basada en un estudio estocástico de la fiabilidad. El estudio comprende primeramente una optimización multiobjetivo donde se busca maximizar la probabilidad de detección del daño en la estructura al mismo tiempo que se busca minimizar los costos de la intervención y garantizar la fiabilidad de la estructura respecto a la probabilidad de falla por corrosión. Luego, los resultados obtenidos del estudio anterior son sometidos a un análisis de eficiencia que permita la minimización de los recursos necesarios y la minimización del tiempo total de inspecciones requerida en la estructura.
El modelo de inspección consta de tres etapas. Primeramente, el nivel de daño por corrosión es modelado considerando la probabilidad de falla y la probabilidad de detección temprana de la corrosión a través de simulación de Monte Carlo. Luego, la segunda etapa busca determinar los tiempos óptimos de inspección a través de la aplicación de algoritmos genéticos que buscan disminuir la probabilidad de falla y disminuir los costos del plan de inspecciones. Finalmente, la última etapa comprende la obtención de la estrategia de inspecciones más adecuada a través de la aplicación del análisis de eficiencia (SFA/MEA) en el proceso. De este modo, el modelo de decisión permite conocer la estrategia de inspección más apropiada desde un enfoque eficiente y sustentable.
2.1. Primera etapa: Modelación del daño por corrosión
En esta primera etapa lo que se busca es determinar el tiempo de inicio de la corrosión en la estructura de hormigón armado. Una vez conocido el tiempo de inicio de corrosión es importante modelar el daño que se produce en la estructura de modo a poder analizar la fiabilidad de la misma desde el punto de vista de la seguridad. Para ello, se ha utilizado una formulación que cuantifica el nivel de daño en un rango de valores que van de cero a uno, en donde se considera la pérdida de la sección transversal de la barra de refuerzo causada por el fenómeno de la corrosión [15]:
|
|
(1) |
Donde D0 es el diámetro inicial de la barra de refuerzo (cm), D(t) es el diámetro de la barra con el paso del tiempo (cm), Vcorr es la tasa de corrosión (cm/año), Ticorr es el tiempo de inicio de corrosión (años) y t es el tiempo de intervención a lo largo de la vida útil de la estructura (años). Entonces, de la expresión anterior se deduce que para que exista daño primeramente debe existir corrosión en la barra. Una manera de determinar el tiempo de inicio de corrosión por carbonatación es la formulación del método de Hakkinen según se muestra en (2).
|
|
(2) |
Donde tcd(d) es el tiempo en años para alcanzar una determinada profundidad de carbonación d (mm), Cenv y Cair son coeficientes ambientales y de aire ocluido respectivamente, a y b son parámetros que dependen del agente aglomerante, y fck es la resistencia característica del hormigón (N/mm2). Por lo tanto, el tiempo de inicio de corrosión se obtiene de (2) fijando el valor de d como un valor critico de profundidad de carbonatación (dcr) para que inicie la corrosión. De esta manera, estudios han demostrado que puede esperarse un inicio del proceso de corrosión cuando el frente de carbonatación se encuentra a una distancia de 5 mm de la barra de refuerzo [16]. Así, el valor de dcr puede ser formulado como el valor de recubrimiento de la estructura menos 5 mm. Determinar este tiempo es esencial para el planeamiento de la inspección ya que el nivel de daño es analizado a partir de este instante hasta el tiempo en que la estructura alcanza la falla [17].
Posteriormente, es importante definir el tiempo para alcanzar la condición de falla en la estructura. La probabilidad de falla puede ser evaluada como una función del tiempo si antes es definida la resistencia residual a través de un proceso estocástico y las características de las cargas en la estructura son conocidas [18]. Desde el punto de vista de la evaluación de la fiabilidad estructural, la falla puede ser evaluada considerando el estado limite último o el estado límite de servicio [19]. Si estos requerimientos no son alcanzados, entonces el sistema puede considerarse en condición de falla. Bajo estos términos, la probabilidad de falla puede ser formulada como:
|
|
(3) |
Donde g(n(t)) es la función de estado limite que define el tiempo para el cual la estructura alcanza un nivel de daño en específico. De esta forma, despejando la expresión de (1), el tiempo de falla (Tf) en años puede ser expresada considerando un nivel crítico de daño (ηcr) por corrosión de la siguiente manera:
|
|
(4) |
La función de estado limite es dependiente del tiempo, es decir, se espera que varíe su valor con el paso del tiempo. De esta manera, la probabilidad de falla no debe ser obtenida como un valor absoluto, sino como un valor relativo que este asociado al tiempo de vida útil de la estructura [20]. Entonces, la condición de falla en una estructura debe ser considerada como la perdida de sus capacidades para cumplir las funciones que son requeridas [21]. En este contexto, estudios han demostrado que cuando el refuerzo registra una pérdida de sección transversal mayor al 25% de su estado original, el mismo podría manifestar cambios en el comportamiento estructural y reducir el margen de seguridad significantemente [22]. Consecuentemente, el nivel de daño critico en este estudio ha sido asumida como ηcr =0.25.
Entonces, considerando la incertidumbre de los parámetros considerados en las ecuaciones previas, el método de la simulación de Monte Carlo puede ser una herramienta útil para obtener la probabilidad de falla en la estructura. De este modo, considerando los tiempos de inicio de corrosión y de falla como funciones no lineales de variables aleatorias, es posible obtener la función de densidad de probabilidad para ambas funciones.
2.2. Segunda etapa: Tiempos óptimos de inspección
Un factor influyente para determinar los tiempos de inspección es la calidad de la técnica de inspección que se está aplicando, la cual comúnmente está caracterizada por la función de probabilidad de detección del daño (detectabilidad). Esta función depende de la intensidad de daño en el cual la técnica de inspección tiene el 50% de probabilidad de detección (ηθ0.5) y su respectiva desviación estándar (σθ). En el caso del daño por corrosión, esta función es comúnmente expresada como [15]:
|
|
(5) |
Donde Φ es la función de distribución acumulativa normal estándar, ηθmin y ηθmax son valores dados que representan el límite de daño para la detectabilidad. Definir un valor acertado para los parámetros considerados en (5) comprende una tarea compleja, por lo que varios estudios [15, 33] asumen dichos parámetros con valores como σθ = 0.1ηθ0.5; ηθmin = 0.7 ηθ0.5 ; ηθmax =1.3 ηθ0.5
Otro de los objetivos principales en el planeamiento de inspecciones es la necesidad de detectar el daño antes que la falla sea alcanzada. Este aspecto es importante no solamente desde el punto de vista de la seguridad, sino también considerando el costo de la intervención cuando el nivel de daño es crítico. Sin embargo, establecer una inspección adecuada es usualmente un gran desafío debido a la dificultad de cuantificar el daño por corrosión en las primeras fases de este fenómeno [23].
Por lo tanto, considerando un conjunto de técnicas de inspección (por ejemplo, técnica A, B y C), una serie de secuencias de inspecciones para todas las posibles combinaciones pueden ser definidas. Es decir, si el planeamiento de inspecciones está definido mediante tres intervenciones durante la vida útil, entonces se podría tener varias secuencias de inspección definidas como AAA, AAB, AAC, ABA, etc. En este contexto, la probabilidad de detección antes de la falla (PρDAF) de una secuencia de inspección (ρ) puede ser formulada considerando la detectabilidad de cada secuencia de inspección (PρD (t)) y la probabilidad de realizar la intervención antes de la falla en la estructura P (ti < Tf). La función para esta probabilidad ha sido definida en [24] y se expresa como:
|
|
(6) |
Donde las probabilidades son consideradas nulas para un tiempo t0 = 0 ya que no existe daño en la estructura. Cuando el daño en una estructura no se trata a tiempo, los costos de mantenimiento tienden a aumentar drásticamente. Es decir, la detección temprana de daños por corrosión también es bastante significativa desde el punto de vista del costo del ciclo de vida. Por este motivo, es necesario que dichos cambios en el rendimiento de la estructura se detecten lo antes posible para que la acción de mantenimiento se lleve a cabo de manera oportuna y minimice los costos del ciclo de vida [25].
Finalmente, esta segunda etapa busca encontrar lo tiempos óptimos de inspección en la estructura de modo a maximizar la probabilidad de detección temprana del daño. Por lo tanto, es necesario realizar una optimización del proceso el cual puede ser formulado como:
|
|
(7) |
donde t0 = 0 y Y es fijado como el tiempo mínimo admisible entre inspecciones consecutivas y T es el tiempo de vida útil de la estructura.
2.3. Tercera etapa: Aplicación del análisis de eficiencia en la optimización multiobjetivo
De modo a poder establecer una optimización multiobjetivo, este estudio incluye, además de la probabilidad de detección temprana de la falla, un análisis de costos de las secuencias de inspección obtenidas en la etapa anterior. Si consideramos un edificio con una vida útil de 50 años, aproximadamente entre el 75 y 80% del costo total se presenta durante la etapa de mantenimiento de la misma [26]. Para satisfacer la función de optimización de (7), es de esperarse que la aplicación de técnicas de inspección de mayor calidad va a ser las que satisfagan la secuencia de inspección más óptima. Sin embargo, una inspección de mayor calidad implica un costo de intervención mayor en las tareas de inspección.
Para una planificación optima de la inspección, es necesario seleccionar la técnica de inspección más adecuada para cada etapa del programa de inspección. Además, el tiempo óptimo entre las inspecciones que se traduce en un menor costo esperado debe considerarse bajo la combinación de técnicas de inspección de diferente calidad [27]. El costo total del planeamiento de inspecciones se obtiene del costo individual de cada técnica de inspección considerada para la secuencia. Para ello, se tiene en cuenta la tasa de descuento neta que permite obtener el Valor Presente Neto del dinero para futuras inversiones durante la vida útil de la estructura. En este sentido, el costo total de la inspección está directamente relacionado con la detectabilidad de la técnica de inspección aplicada y el número de intervenciones realizadas durante la vida útil de la estructura [28]. Entonces, para una secuencia de inspección dada, el costo de la secuencia en el tiempo de intervención viene dado por:
|
|
(8) |
Donde αρiinsp es el costo de la secuencia asociado a una técnica de inspección determinada, el cual es asumido como una fracción del costo total inicial (C0) de la estructura, r es la tasa de descuento neto. Entonces, los tiempos óptimos de inspección deben ser formulados considerando el tiempo para el cual se logra un balance entre la máxima probabilidad de detección (PDρ) y un mínimo costo de inspección (Cρ). Es decir, el principal objetivo de estas formulaciones seria evitar la ocurrencia de la falla en la estructura a un menor costo posible. Por lo tanto, el problema de optimización multiobjetivo puede ser modelado, bajo las mismas restricciones de (7), de la siguiente manera:
|
|
(9) |
El problema de optimización anterior generalmente se resuelve mediante métodos de optimización de gradiente tales como algoritmos genéticos o clasificación no dominada en algoritmos genéticos (NSGA-III). Sin embargo, este enfoque no considera los recursos necesarios para la implementación de las inspecciones o los costos administrativos indirectos, ni proporciona una clasificación relativa ordenada que permita determinar cuáles son las mejores secuencias. De modo a compensar esa limitación en la optimización, esta investigación propone la aplicación de un análisis de eficiencia a los resultados obtenidos de la optimización de (9).
Para este análisis de eficiencia, se proponen dos nuevas variables que deberán ser analizadas como variables de entrada en el análisis. Estas variables son la cantidad de diferentes técnicas de inspección necesarias para una determinada secuencia (Nρ) y la "ventana" de inspecciones de la secuencia (Vρ), es decir, el tiempo entre la primera y la última inspección en la estructura. Estas variables son fundamentales para la gestión ya que los gerentes siempre buscan implementar la menor cantidad de recursos (técnicas de inspección) en un menor tiempo posible que le permitan obtener el mismo resultado óptimo para un planeamiento de inspección dado.
Entonces, el análisis de eficiencia lo que busca básicamente es analizar la variación de una serie de parámetros de entrada para obtener un determinado valor de salida, considerando una función de frontera que agrupa los resultados según sean eficientes o no. Por lo tanto, una determinada secuencia de inspección tendrá un valor después del análisis de eficiencia en un rango de 0 a 1, donde mientras más cercano a uno sea su valor, más eficiente será dicha secuencia.
En las dos primeras etapas definidas en este trabajo, para una secuencia dada es posible asociar una serie de valores de salida y de entrada. Los métodos de eficiencia aplicados en este estudio pueden cambiar respecto a un conjunto de variables complementarias elegidas para el análisis. Así, en este estudio el modelo de retorno de variables a escala es considerada para la medición de la eficiencia [29], donde se define el conjunto mediante la expresión:
|
|
(10) |
Donde N es el número de secuencias bajo estudio y ΛN es el conjunto de soluciones eficientes. Luego, el valor del análisis de eficiencia es obtenido a través de la resolución de problemas de optimización lineal que dan como resultado la solución global del análisis. Entonces, el valor de eficiencia (entre 0 y 1) es obtenido mediante la contribución direccional de cada variable de entrada y de salida, donde, para la entrada y la salida, se mide la contribución en la secuencia a través de indicadores establecidos para cada método de eficiencia implementado. La derivación matemática de ambos métodos comprende un desarrollo extenso que va más allá del objetivo principal de este artículo. Por esta razón, para una información más detallada los autores recomiendan revisar otros estudios como [29-31].
3. Resultados
De modo a poder ilustrar la aplicabilidad del modelo de decisión formulado se ha considerado su aplicación en un caso hipotético. Esta sección se ha desarrollado de modo a establecer la importancia del análisis de eficiencia en el planeamiento de las inspecciones de edificios. Se ha supuesto una estructura de hormigón armado con una vida útil estimada de 50 años (T=50) y el análisis de costo se ha considerado en base a costos referenciales de modo a darle una simplicidad al estudio. Entonces, estos costos están relacionados al costo inicial de la construcción el cual se ha establecido en 1000 unidades de costo (C0 = 1000). A su vez, la tasa de descuento neto para el análisis de costos ha sido asumida como 5.5%.
En la primera etapa, la función de densidad de probabilidad para los tiempos de inicio de corrosión y el tiempo de falla fueron obtenidos después de aplicar el método de simulación de Monte Carlo. En esta simulación fueron considerados parámetros cuya aleatoriedad fue asumida según otros estudios y se muestran en la Tabla 1. En esta simulación se han considerado 100000 iteraciones donde los resultados se obtuvieron al subdividir la región de muestreo en 2000 regiones espaciadas uniformemente en las que se calcula el número de ocurrencias (fallas) para cada región.
Tabla 1 Parámetros utilizados para la simulación de Monte Carlo
|
|
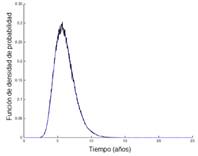
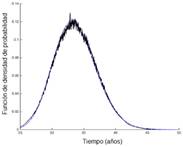
El comportamiento aleatorio de las variables de la Tabla 1 fueron asumidos con una distribución LogNormal considerando que es usada frecuentemente en estudios de ingeniería civil cuando las variables tienen una distribución desconocida [32]. Sin embargo, para establecer la distribución más adecuada para cada variable conllevaría un análisis exhaustivo basado en datos reales, lo cual va más allá del objetivo de este trabajo. De este modo, después de realizar la simulación de Monte Carlo, la distribución de probabilidades asociadas al tiempo de inicio de corrosión y tiempo de falla fueron obtenidas y se muestran en la Fig. 1.
Las variables consideradas para el cálculo de inicio de corrosión por carbonatación fueron extraídas del Anexo 9 de la normativa EHE-08 y corresponden a una estructura de hormigón con cemento Portland (a =1800; b=1.7), un elemento estructural expuesto a la intemperie (Cenv =1), y un hormigón con contenido de aire menor a 4.5% (Cair =1). Por lo tanto, para este análisis, los parámetros geométricos de la distribución indican que el tiempo de inicio de la corrosión podría esperarse en promedio a los 5.731 años de vida útil de la estructura bajo las condiciones asumidas.
Por otro lado, la falla esperada por corrosión en la estructura se alcanzaría a los 31.756 años de vida útil, lo cual implica el desuso de la estructura por degradación crítica.
|
|
|
|
|
|
Fig. 1. Función de densidad de probabilidad para (a) Tiempo de inicio de corrosión y (b) Tiempo de falla
En la segunda etapa, el análisis busca determinar los tiempos óptimos de inspección considerando los resultados de la etapa anterior en conjunto con algunas características de las técnicas de inspección comúnmente utilizadas para determinar el daño por corrosión en las estructuras de hormigón armado. Para ello, la capacidad que tiene cada una de estas técnicas para detectar el daño se vuelve fundamental en esta etapa. Sin embargo, esta característica está directamente relacionada con la calidad de la técnica aplicada y, a su vez, el costo total del planeamiento de la inspección. Por lo tanto, es fundamental encontrar un equilibrio entre el costo de la intervención en la estructura y la calidad de la misma.
En la práctica, determinar la capacidad de detección de cada técnica de inspección es una tarea compleja ya que intervienen diversos factores tales como la condición de la estructura, la experiencia del técnico interventor, la calibración del equipamiento, el mecanismo de degradación, entre otros. Por esta razón, los valores que determinan las características de las técnicas de inspección fueron asumidas en base a su capacidad esperada. En este estudio, se consideraron tres técnicas de inspección para detectar la corrosión en la armadura de refuerzo: la medición del potencial de media celda, la resistencia a la polarización lineal, y la resistividad del hormigón. Los parámetros asumidos para cada una de estas técnicas se presentan en la Tabla 2.
Tabla 2 Parámetros para cada técnica de inspección
|
|
Los parámetros considerados en la tabla anterior pueden ser reajustados según cada caso, y considerando que se utilizan costos referenciales, el modelo formulado puede ser adaptado a cualquier otro mercado en otro país, aunque los valores necesitaran ser reajustados para ello. Además, la versatilidad del modelo permite que los parámetros que definen las características de cada técnica de inspección puedan ser reajustados a medida que se va recabando mayor información sobre sus capacidades para detectar el daño.
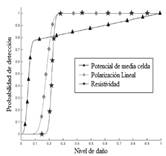
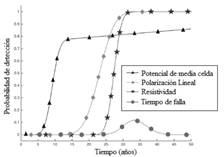
En la Fig. 2 se muestra el primer resultado después de computar y resolver las formulaciones matemáticas de la Sección 2. Estas formulaciones fueron programadas en el software MATLAB versión R2015a para poder obtener la curva de distribución acumulada de la función de detectabilidad para cada técnica de inspección, tal como se muestra en la Fig. 2(a). Esta curva representa la probabilidad de detección con relación al nivel de daño presentado en la estructura. En este caso, para los valores asumidos en la Tabla 2, la técnica de menor calidad (mayor valor de η0.5) es la inspección por ensayo de resistividad, mientras que el ensayo de potencial de media celda es el que presentó una mayor detectabilidad. Por otro lado, en la Fig. 2(b) es posible interpretar el comportamiento de la función de detectabilidad a lo largo de la vida útil de la estructura. Así, es posible visualizar claramente las capacidades que posee cada técnica de inspección de detectar el daño antes de la falla.
|
|
|
|
|
|
Fig. 2. Función de densidad acumulada para la detectabilidad de las técnicas de inspección
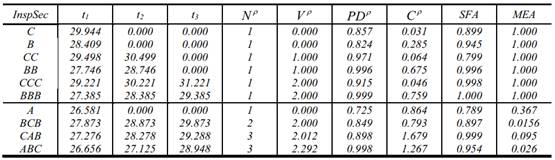
El último paso del modelo propuesto para la planificación de la inspección implica la optimización de múltiples objetivos a través de un análisis de eficiencia. Este proceso da como resultado tiempos óptimos para aplicación de las intervenciones y la técnica más adecuada para cada instante. Los resultados de este proceso se presentan en la Tabla 3. Esta tabla muestra la secuencia óptima para cada técnica de inspección (InspSec); los tiempos óptimos de las inspecciones en años (t1, t2, t3); el número de técnicas requeridas para la secuencia (Nρ); el tiempo total del planeamiento de la inspección en años (Vρ); la máxima probabilidad de detección de daño antes de la falla (PDρ); el costo total del planeamiento de la inspección establecida como costo referencial (Cρ); y los resultados del análisis de eficiencia (SFA/MEA). Para estos dos últimos parámetros de la tabla, cuanto más cerca de 1 este el valor, más eficiente es la secuencia de inspecciones.
Tabla 3 Resultados del análisis de eficiencia para el planeamiento óptimo de inspecciones
|
|
Los resultados de la Tabla 3 representa el propósito principal de este estudio. Como puede verse, a diferencia de otros estudios en los que solo se aplican técnicas de optimización, el resultado del análisis de eficiencia permite saber con claridad cuál es la mejor estrategia que se debe implementar para la planificación de la inspección. Una discusión más detallada se aborda en la siguiente sección con respecto a este resultado obtenido.
4. Discusión de los resultados
El planeamiento óptimo de las inspecciones ha sido alcanzado en este trabajo a través de un modelo de decisión que abarca tres etapas principales: la determinación de los tiempos de inicio de corrosión y falla en la estructura, la probabilidad de detección temprana del daño, y la formulación de la secuencia optima de inspecciones a través de un análisis de eficiencia.
En este estudio se ha visto que el tiempo de inicio de la corrosión depende principalmente del espesor de recubrimiento de la estructura y de la calidad de la misma que, en este caso, ha sido establecida según su resistencia característica a la compresión. Cuanto mayor sean estos dos parámetros, mayor será el tiempo de inicio de corrosión por carbonatación. Considerando este mecanismo de degradación, la exposición ambiental es otro factor determinante para el inicio de la corrosión. Los factores ambientales tales como la humedad relativa, la temperatura y la concentración atmosférica de dióxido de carbono afectan la tasa de degradación de estas estructuras.
El tiempo de falla ha sido considerado como aquel instante para el cual la perdida de sección transversal del refuerzo por corrosión reduce el margen de seguridad considerablemente, es decir, una reducción de sección mayor al 25% de su sección inicial. Esta reducción de la sección afecta significativamente la capacidad estructural debido a una disminución de la adherencia entre acero y concreto. Sin embargo, cabe resaltar que la falla en la estructura considerada en este estudio no implica una situación de colapso, sino solamente que la seguridad estructural podría estar comprometida. También, del conjunto de parámetros considerados en la función de estado limite, la tasa de corrosión ha sido la más influyente en el tiempo de falla, ya que cuanto mayor sea la misma, el tiempo de falla se presenta de manera más prematura en la estructura.
Otro factor fundamental en el estudio ha sido la detección a tiempo del daño por corrosión en la estructura. Si la detección es tardía (próximo al daño critico), una intervención de reparación en la estructura podría llevar a una elevada inversión que incidiría directamente en el costo total del ciclo de vida de la estructura. Bajo este enfoque, uno de los puntos claves del modelo de decisión desarrollado fue la detección temprana del daño, el cual está directamente relacionado con la detectabilidad de las técnicas de inspección aplicadas en la estructura. Por esta razón, es importante que los valores asumidos (η0.5; σ) para cada técnica de inspección sean actualizados después de cada intervención y generar al mismo tiempo una base de datos que permita refinar la detectabilidad de cada técnica.
Del resultado obtenido y mostrado en la Fig. 2(a) puede notarse que la técnica de potencial de media celda tiene, a priori, una elevada detectabilidad ya que necesita un menor nivel de corrosión en el refuerzo para detectar el daño. En contraste, la inspección por resistividad se muestra como la menos adecuada considerando este parámetro. Sin embargo, la calidad de una técnica de inspección no está establecida solamente por un simple parámetro, sino que son múltiples parámetros los que finalmente determinan su detectabilidad. Así, en la Fig. 2(b) puede verse la variación de la detectabilidad de cada técnica de inspección a lo largo de la vida útil de la estructura. Por lo tanto, puede verse que los ensayos de resistencia a la polarización y resistividad eléctrica, a pesar de no tener una elevada detectabilidad inicial, a lo largo del tiempo estos adquieren una detectabilidad mayor que el ensayo de potencial de media celda. Esta controversia de criterios es frecuente en casos reales donde tomar de antemano una decisión adecuada respecto a la mejor técnica de inspección a ser empleada es compleja.
En un modelo de toma de decisiones, la controversia entre los criterios no permite saber de antemano qué solución es la más aconsejable. Por ejemplo, desde un punto de vista lógico, podría esperarse que una técnica de inspección de alta calidad registraría una mayor detectabilidad. Por otro lado, teniendo en cuenta que la detectabilidad no está relacionada únicamente con la calidad de la técnica, la intervención en una estructura puede exceder los costos del presupuesto si solo se aplican técnicas de alta calidad. Por este motivo, es necesario realizar un análisis detallado que permita establecer una compensación de costo-efectividad de cada técnica de inspección propuesta para aplicarla a lo largo de la vida útil de una estructura.
Considerando lo anterior, la última etapa del modelo de decisión formulado en este trabajo establece un análisis de eficiencia que garantiza cuantitativamente una compensación costo/eficiencia del planeamiento de la inspección. Este tipo de análisis permite, además de optimizar los recursos necesarios para satisfacer las funciones objetivo, determinar cuál es la mejor opción de entre un conjunto de soluciones óptimas. Después de aplicar ambos métodos de eficiencia (SFA/MEA), se ha podido constatar que el método MEA considera un análisis más amplio permitiendo así evaluar varios parámetros de entrada y salida en el proceso.
De los resultados mostrados en la Tabla 3 puede verse la importancia del análisis de eficiencia en el contexto del estudio. Por ejemplo, para la secuencia ABC es obtenida uno de los mejores resultados desde el punto de vista de la probabilidad de detección temprana del daño. No obstante, después de aplicar el análisis de eficiencia, esta secuencia muestra uno de los peores resultados.
Además, puede notarse en la misma tabla que una secuencia de inspección puede ser optima y efectiva sin que sea necesario realizar varias intervenciones en la estructura y sin la necesidad de utilizar una amplia variedad de técnicas de inspección. Este resultado es muy significante no solo para la competitividad de una empresa constructora, sino también desde el punto de vista ambiental y de la sustentabilidad de la estrategia de mantenimiento. Intervenir repetidas veces una estructura implica un consumo extra de recursos humanos y materiales, lo cual incide negativamente ya que la reparación de estructuras de hormigón generalmente implica el uso de cemento, cuya fabricación está asociada a un alto impacto ambiental.
Por último, de modo a verificar la robustez del modelo de decisión formulado, se ha simulado todo el proceso nuevamente duplicando el valor de la tasa de corrosión asumida en la Tabla 1. Los resultados mostraron que claramente el análisis de eficiencia es fundamental para el planeamiento de las inspecciones. Por ejemplo, con la nueva simulación se ha visto que, para una secuencia de inspección denotada por BCA, la probabilidad de detección temprana fue de 0.991; mientras que para una secuencia de inspección CC, el valor correspondiente fue de 0.989. En este caso, ambas secuencias presentan valores similares, lo cual dificulta la toma de decisiones respecto a cuál es la secuencia de inspección más apropiada. Sin embargo, el valor obtenido por la aplicación del método MEA permitió determinar que la secuencia CC tiene un valor de eficiencia igual a 1, mientras que la eficiencia de la secuencia BCA era solamente de 0.037.
Además, como era de esperarse, al aumentar el valor de la tasa de corrosión los nuevos tiempos inspección fueron menores a los valores de la Tabla 3. Sin embargo, de estos resultados fue posible observar que la disminución de los tiempos de inspección no fue proporcional al incremento del valor de la tasa de corrosión. Esto significa que no hay una relación lineal entre los parámetros considerados por el modelo de decisión y los resultados obtenidos. Esto es muy importante porque permite al modelo representar de manera más apropiada la incertidumbre del mecanismo de degradación.
5. Conclusión
Esta investigación ha demostrado que es posible lograr resultados altamente eficientes para la planificación de la inspección. Dicha eficiencia se evidencia aplicando la menor variedad de técnicas de inspección disponibles en un período de tiempo más corto. Esto evita el desperdicio de recursos que pueden colaborar indirectamente con la reducción del impacto ambiental asociado con el sector de la construcción y la sostenibilidad de las infraestructuras.
A través de un restablecimiento de los datos de entrada, el método de toma de decisiones abordado en este documento puede aplicarse para la planificación de la inspección de otros tipos de estructuras sometidas a otros mecanismos de degradación. De esta manera, los estudios futuros sobre la gestión del mantenimiento pueden implementar los mismos métodos de análisis de eficiencia, pero teniendo en cuenta otros recursos que dan mejores resultados con este enfoque. No obstante, debe mencionarse que se necesitan más estudios que permitan, a través de estudios de casos reales, ajustar los parámetros de las diferentes técnicas de inspección que se han asumido de forma genérica en esta investigación.
Referencias
[1] Correa E, Peñaranda S, Castaño J, Echeverria F. “Concrete deterioration in Colombian urban atmospheres”. Revista Facultad De Ingeniería - Universidad De Antioquia. 2010; (52), pp. 41-6.
[2] Fan Y., Hu Z., Zhang Y., Liu J . “Deterioration of compressive property of concrete under simulated acid rain environment”. Construction and Building Materials. 2010; 24(10), pp. 1975-83. doi:10.1016/j.conbuildmat.2010.04.002.
[3] Folic R. “Durability design of concrete structures, Part 1: Analysis fundamentals”. Architecture and Civil Engineering. 2009; 7(1), pp. 1-18. doi:10.2298/FUACE0901001F.
[4] Roque J, Moreno Junior A. “Consideraçoes sobre vida útil do concreto”. 1er Encontro Nacional de PesquisaProjeto-Produçao em Concreto Pre-moldado. Sao Carlos, Brasil.; 2005, p. 1-12. doi:10.1590/S0034-89102007000900003.
[5] Dyer T. “Concrete Durability”. Florida: Taylor & Francis Group; 2014. ISBN 9780203862117.
[6] Ekolu SO. “A review on effects of curing, sheltering, and CO2 concentration upon natural carbonation of concrete”. Construction and Building Materials. 2016; 127, pp 306-20. doi:10.1016/j.conbuildmat.2016.09.056.
[7] Endrenyi J, Aboresheid S, Allan RN, Anders GJ, Asgarpoor S, Billinton R, et al. “The present status of maintenance strategies and the impact of maintenance on reliability”. IEEE Transactions on Power Systems 2001; 16(4), pp. 638-46. doi:10.1109/59.962408.
[8] Kim S, Frangopol D. “Decision making for probabilistic fatigue inspection planning based on multi-objective optimization”. International Journal of Fatigue. 2018; 111, pp. 356-68. doi:10.1016/j.ijfatigue.2018.01.027
[9] Malioka V. “Condition indicators for the assessment of local and spatial deterioration of concrete structures”. 2009. doi: 10.3929/ethz-a-006077800.
[10] Mutz R, Bornmann L, Daniel HD. “Are there any frontiers of research performance? Efficiency measurement of funded research projects with the Bayesian stochastic frontier analysis for count data”. Journal of Infometrics 2017; 11(3), pp. 613-28. doi:10.1016/j.joi.2017.04.009.
[11] Coelli T, Prasada Rao D, O'Donnell C, Battese G. “An introduction to efficiency and productivity analysis”. New York, USA.: Springer; 2005. ISBN 0-387-25895-7.
[12] Holmgren J. “The effects of using different output measures in efficiency analysis of public transport operations”. Research in Transportation Business & Management. 2018; (February). doi:10.1016/j.rtbm.2018.02.006.
[13] Novaes A, Silveira S, Medeiros H. “Efficiency and productivity analysis of the interstate bus transportation industry in Brazil”. Pesquisa Operacional. 2010; 30(2), pp. 465-85.
[14] Fernández-López XL, Coto-Millán P. “From the Boom to the Collapse: A Technical Efficiency Analysis of the Spanish Construction Industry during the Financial Crisis”. Construction Economics and Building 2015; 15(1), pp. 104-17. doi:10.5130/ajceb.v15i1.4168.
[15] Frangopol D, Lin K, Estes A. “Life-Cycle Cost Design of Deteriorating Structures”. Journal of Structural Engineering. 1997; 123(10), pp. 1390-401.
[16] Yoon I, Copurolu O, Park K. “Effect of global climatic change on carbonation progress of concrete”. Atmospheric Environment. 2007; 41, pp. 7274-85. doi:10.1016/j.atmosenv.2007.05.028
[17] Tuutti, K. “Corrosion of steel in concrete”. Stockholm: Swedish Cement and Concrete Research Institute. 1982
[18] Ellingwood B, Mori Y. “Reliability-based service life assessment of concrete structures in nuclear power plants: optimum inspection and repair”. Nuclear Engineering and Design. 1997; 175, pp. 247-58.
[19] Afzal N, Bjerva M, Henriksen E, Lindgren G. “Reliability Analysis of Reinforced Concrete using Non-Linear Finite Element Analysis”. Master thesis; NTNU - Norwegian University of Science and Technology; 2016.
[20] Neves R, Branco F, Brito J. “A method for the use of accelerated carbonation tests in durability design”. Construction and Building Materials 2012; 36, pp. 585-91.
[21] International Standard ISO 15686-1. “Buildings and constructed assets - service life planning - Part 1: General Principles”. International Standard Organization, 2000.
[22] Cheung M, So K, Zhang X. “Life cycle cost management of concrete structures relative to chloride induced reinforcement corrosion”. Structure and Infrastructure Engineering. 2012; 8(12), pp. 1136-50. doi:10.1080/15732479.2010.507474.
[23] Patil S, Karkare B, Goyal S. “Corrosion induced damage detection of in-service RC slabs using acoustic emission technique”. Construction and Building Materials. 2017; 156, pp. 123-30. doi:10.1016/j.conbuildmat.2017.08.177.
[24] Soliman M, Frangopol D, Kim S. “Probabilistic optimum inspection planning of steel bridges with multiple fatigue sensitive details”. Engineering Structures 2013; 49, pp. 996-1006. doi:10.1016/j.engstruct.2012.12.044
[25] Moughty J, Casas J. “A State of the Art Review of Modal-Based Damage Detection in Bridges: Development, Challenges, and Solutions”. Applied Sciences. 2017; 7, pp. 1-24. doi:10.3390/app7050510.
[26] Madureira S, Flores-Colen I, de Brito J, Pereira C. “Maintenance Planning of Pitched Roofs in Current Buildings”. Construction and Building Materials 2017; 147, pp. 790-802. doi:10.1061/(ASCE)CO.1943- 7862.0001316.
[27] Sheils E, O'Connor A, Breysse D, Schoefs F, Yotte S. “Development of a two-stage inspection process for the assessment of deteriorating infrastructure”. Reliability Engineering and System Safety. 2010; 95(3), pp. 182-94. doi:10.1016/j.ress.2009.09.008.
[28] Mori Y, Ellingwood B. “Maintainin g reliability of concrete structures. I: Role of Inspection/Repair”. Journal of Structural Engineering. 1994; 120(3), pp. 824-45.
[29] Bogetoft P, Hougaard J. “Efficiency Evaluations Based on Potential (Non-Proportional) Improvements”. Journal of Productivity Analysis. 1998; 12, pp. 233-47.
[30] Charnes A, Cooper W, Rhodes E. “Measuring the efficiency of decision making units”. European Journal of Operational Research. 1978; 2(6), pp. 429-44. doi:10.1016/0377-2217(78)90138-8.
[31] Ramli N, Munisamy S, Arabi B. “Scale directional distance function and its application to the measurement of eco-efficiency in the manufacturing sector”. Annals of Operations Research. 2013; 211(1), pp. 381-98. doi:10.1007/s10479-013-1441-1.
[32] Xu Y, Qian Y, Chen J, Song G. “ Probability-based damage detection using model updating with efficient uncertainty propagation”. Mechanical Systems and Signal Processing. 2015; 60-61, pp. 958-70. doi:10.1016/j.ymssp.2014.11.008.
[33] Kim S, Frangopol D. “Inspection and monitoring planning for RC structures based on minimization of expected damage detection delay”. Probabilistic Engineering Mechanics. 2011; 26(2), pp. 308-20. doi:10.1016/j.probengmech.2010.08.009.