1.
Introducción
En la actualidad, la ciencia se está convirtiendo cada vez
más en una fuerza productiva directa de la sociedad, lo que hace que las
investigaciones aplicadas se encaminen a mejorar y elevar la eficiencia
económica de los procesos industriales, la calidad de los productos y la
productividad.
Crece incesantemente el empleo de las computadoras para la
dirección de los procesos tecnológicos, pues la esencia de esta etapa de la
Revolución Científico Técnica es que funciones hasta ahora realizadas por el
hombre comienzan a ser obra de las máquinas.
Las ciencias modernas han desarrollado las ideas de la
simulación, los métodos de análisis y síntesis de los sistemas, por lo que la
modelación matemática, interpretada, como la representación de la verdad
relativa de un lado del fenómeno, pertenece al campo de las ciencias, que
estudia la cibernética matemática y es un fruto del desarrollo científico moderno,
dado que las ideas de cada época se ven en sus técnicas. [1]
La ciencia y la introducción de los resultados científicos
en la producción, adquieren relevantes funciones sociales por lo que deberán
estar orientadas al desarrollo armónico y proporcional de la ciencia de manera
que contribuya al desarrollo integral de la técnica, la producción y la
economía [2].
El objetivo de este trabajo fue
conceptualizar el análisis de sistemas incluyendo simulación y modelación
matemática para representar los problemas de la industria química buscando
intensificar sus instalaciones.
2.
Materiales y métodos.
El método de investigación aplicado fue la revisión
sistemática de literatura sobre el tema. En el acopio de la documentación
requerida se utilizó el motor de búsqueda Google, con el cual fue posible
registrar publicaciones seriadas, resultados de investigación y libros. La
revisión y análisis del acervo documental obtenido se interpretó
cualitativamente.
3. Resultados y discusión
Teoría de los Sistemas y Modelación Matemática
La revolución científico técnica moderna da inicio a la era de la revolución
automatizada, de manera que las
ciencias se transforman en una fuerza productiva directa.
La complejidad del desarrollo tecnológico
exige que para abordar las
tareas técnicas contemporáneas, se considere que la
ciencia se adelanta a la técnica y a la producción en su desarrollo. Se plantea
cada
vez
de forma más
aguda
los problemas vinculados a la
síntesis
de los
conocimientos, a la
elaboración
lógica de
la información, siendo de carácter integral el
rasgo
específico del desarrollo de las ciencias modernas, lo que
es expresión de la dialéctica del objeto mismo, dando vida a los diversos
métodos de síntesis de
los conocimientos relativos a diferentes ciencias. A la par y por ello en las ciencias modernas el
estudio de los
sistemas poseedores de
propiedades
comunes,
se ha difundido ampliamente, planteando
el problema
de la elaboración de la metodología de las investigaciones sistemáticas. Esta necesidad del desarrollo ha sido satisfecha con los métodos matemáticos, que con la simulación de los fenómenos se interese por
una
de las cualidades del pensamiento humano:
la previsión y el
pronóstico;
por lo que los métodos matemáticos imprimen
un carácter cualitativamente distinto al progreso técnico.
Con el desarrollo de la cibernética fueron ampliándose sus
aplicaciones, y se concrete una definición general más apropiada
como la dada por Klaus (1974) como "la teoría de las relaciones de
posibles sistemas dinámicos auto
regulados con las partes que
lo componen" o una
más general y menos comprometedora sería: “la cibernética es la ciencia de
los
sistemas cibernéticos". [3]
El método científico de investigación aplicable
a todas las esferas de las ciencias y
la técnica, es la teoría
de los sistemas, pues
la
teoría de los sistemas es
un método general de investigación
científica que transforma los
distintos principios de la metodología de investigación de tal forma que estos adquieren
significado heurístico
en el
conocimiento científico especializado. [4]
La teoría de los sistemas surge
como
una necesidad de la matemática
al estudiar los sistemas Así, esta comprende la teoría que se ocupa de las relaciones entre la estructura y la función del sistema y las interacciones entre las partes y el todo del sistema.
Para
Kafarov (1976), la matemática de los procesos de la industria química
se
ocupa de las relaciones entre
los equipos de los procesos
continuos (relaciones entre
elementos del
sistema), así
como
las uniones entre los
equipos y sus partes y además, del comportamiento del sistema dependiendo de la influencia del ambiente (relaciones entre estructura y función). [5]
En la teoría de los sistemas, el análisis de los mismos es la metódica
para la obtención de los resultados
en el
estudio
activo, es decir, la acción y dirección de
un sistema,
para ello se
requieren, métodos de
modelación que sean capaces de
representar los aspectos y rasgos que se desean estudiar en el comportamiento de los sistemas.
La Teoría de los
Sistemas,
que junto con
la teoría de
la información, la teoría de la regulación,
la teoría
de los
juegos y
la teoría de
los algoritmos, conforman la cibernética, tiene como concepto central el de "sistema", aunque
una
definición
general
de sistema se
hace difícil; podemos referirnos a la de Kafarov (1976): La totalidad de los procesos químicos
físicos que se desarrollan, así como los medios técnicos que lo posibilitan. [5]
Desde el punto de vista
de
la cibernética son los sistemas dinámicos los que se estudian como parte de ella.
Las
propiedades generales
que
estos poseen son las siguientes:
1) Integridad, 2) Complicación.
3) Estabilidad dinámica multidimensional.
4) Controlabilidad. 5)
Transición en el tiempo.
6) Procesamiento y almacenamiento de la información,
7) Estructura jerárquica. 8) Independencia relativa de las
partes del sistema, 9) Diferenciabilidad cualitativa de los elementos.
Clasificación de los Sistemas.
La clasificación
de los modelos matemáticos dinámicos complejos
puede efectuarse desde diferentes principios. Seguiremos el siguiente: [6]
Sistemas Cerrados: aquellos
en que
existen solamente elementos internos. Las salidas de sus
elementos
son al
mismo
tiempo
entradas de otros.
Sistemas Abiertos: son aquellos en los cuales por lo menos un elemento
no tiene entrada o salida a otro elemento.
Sistemas lineales: entre las salidas y las entradas del sistema
existen relaciones lineales.
Sistemas no lineales: no existen relaciones lineales entre las salidas
y las entradas del sistema, estos sistemas bajo determinadas
consideraciones pueden llegar a linealizarse.
Sistemas determinísticos: son aquellos en los
cuales las
variables que
los
describen cambian de acuerdo con regularidades
fijadas exactamente, así como que sus valores estén fijos determinan
claramente el estado del sistema.
Sistemas estadísticos: las variables del
sistema
son
variables
casuales, cuya
distribución es desconocida pero que pueden
conseguir por medio de la
información de muestras.
Sistemas estocásticos: Son aquellos sistemas estadísticos donde las variables que lo escriben dependen de otro parámetro t (en general el tiempo), o sea que está en presencia de variables casuales con variación con respecto al tiempo.
Sistemas discretos: aquellos
en los
cuales cada variable del sistema puede tomar una serie de valores Ci; i: 1, 2, 3..., y,
para
ello los Ci permanecen aislados, o sea que para cada Ci existe un ambiente, que no
puede
existir otro Cj; J = i de dicha variable C.
Sistemas Continuos: son aquellos en los cuales cada variable del
sistema puede tomar
todos
los valores posibles en un intervalo
determinado. De acuerdo a su carácter se pueden diferenciar sub sistemas cualitativos del sistema global como sigue:
a) Sistemas de masas, b) Sistemas de energía. d) Sistemas de información.
Partiendo de las definiciones anteriormente dadas, puede
concluirse con las siguientes ideas básicas sobre los sistemas:
·
Se crea con un
objetivo preciso. Este objetivo condiciona al sistema, así como a su actividad
y a su conformación interna, por tanto a su complejidad.
·
Los
sistemas de procesos
tienen la
función de
realizar
transformaciones industriales de
masa y energía.
·
Los
elementos
que componen el sistema
de procesos se
agrupan,
en
procesos de transformación de
energía y masa para el transporte y almacenamiento de ellas.
·
Las relaciones se componen de las corrientes de masa y energía que crean
los acoples entre los elementos del sistema.
·
Los sistemas
cibernéticos poseen características homeostáticas, es decir, son
capaces de conservar la estabilidad de sus parámetros fundamentales pese a los
cambios del medio
·
Los sistemas pueden
ser descrito por un conjunto de variables que reflejan determinadas propiedades
de los elementos del mismo
·
Entre el sistema y el
medio y a la vez entre los diferentes subsistemas existen canales a través de
los cuales se transmite información
·
La organización o
acoplamiento de los subsistemas de un sistema se realiza a partir de tres tipos
de flujos fundamentales: secuenciales, en paralelo y retroalimentación.
Los planos de
consideración de los sistemas de procesos
son: [2]
a) Grupos de unidades,
b) Etapas de
Procesos,
c) Procesos completos,
d) Fábricas de
transformación de materiales,
e) Sistemas combinados de transformación de materiales,
Por otro lado, los elementos de un sistema pueden clasificarse de acuerdo a:
1. Número de unidades de entrada y salida,
2. De acuerdo
con el
comportamiento en
el tiempo.
3. Según las variables de
decisión, e) Según la función técnica del proceso
Los sistemas de procesos pueden clasificarse
en dos grupos:
1. Según la
función en:
a) Sistema para la
transformación de
materiales,
b) Sistemas para
el
suministro de materiales auxiliares,
c) Sistemas para
el
suministro de energía,
d) Sistemas de información
2. Según la estructura en:
a) Acople en serie,
b) Acople en cascada,
c) Acople en paralelo,
d) Acople de desviación,
e) Acople de recirculación
Análisis de Sistemas.
El Análisis de Sistemas trata básicamente de determinar
los objetivos y límites del sistema objeto de análisis, caracterizar su
estructura y funcionamiento, marcar las directrices que permitan alcanzar los
objetivos propuestos y evaluar sus consecuencias. Dependiendo de los objetivos
del análisis se pueden encontrar dos problemáticas distintas:
·
Análisis de un sistema
existente para comprender, mejorar, ajustar y predecir su comportamiento.
·
Análisis como paso
previo al diseño de un nuevo sistema-producto.
El Análisis de Procesos Tecnológicos se puede realizar
bajo un aspecto limitado, unilateral del proceso, o con un enfoque multilateral
más complejo.
Los Análisis Parciales, aunque son también necesarios
para la economía de las empresas, sólo brindan soluciones parciales, que no
necesariamente tienen que coincidir con las que se logran con un enfoque
multilateral más complejo, que por otro lado requiere de la participación de
personal calificado de varias ramas de la ciencia que laboren de forma
coordinada en la búsqueda de las reservas del proceso estudiado. [7]
En la literatura internacional se reportan numerosas
referencias a diferentes análisis parciales, un amplio campo de estos trabajos
lo ocupan, los análisis de las condiciones tecnológicas en los procesos de la
industria química concentrándose en la influencia de la conducción y la
selección del parámetros del proceso sobre el incremento de las capacidades de
producción; sobre la fiabilidad de los procesos; sobre los consumos específicos
de producción y los balances de materiales y energía. Los incrementos de las
capacidades de producción deben sustentarse a programas de intensificación o
llámese de mejoras y que depende de la particularidad de cada industria.
En cualquier caso, se pueden agrupar formalmente las
tareas que constituyen el análisis en una serie de etapas que se suceden de
forma iterativa hasta validar el proceso completo:
Conceptualización: Obtener una
visión de muy alto nivel del sistema, identificando sus elementos básicos y las
relaciones de éstos entre sí y con el entorno.
Análisis funcional: Describe
acciones y transformaciones que tienen lugar en el sistema, las cuales se
describen como funciones que reciben entradas y producen salidas.
Análisis de condiciones (o constricciones): Debe
reflejar todas las limitaciones impuestas al sistema que restringen el margen
de las soluciones posibles. Estas se derivan a veces de los propios objetivos
del sistema:
·
Operativas:
restricciones físicas, ambientales, de mantenimiento, de personal, etc.
·
De calidad:
fiabilidad, mantenibilidad, seguridad, convivencialidad, etc.
En ciertos casos se presentan limitaciones en los
recursos utilizables:
·
Económicos, reflejados
en un presupuesto.
·
Temporales, que
suponen unos plazos a cumplir.
·
Humanos.
·
Metodológicos, que
conllevan la utilización de técnicas determinadas.
·
Materiales, como
espacio, herramientas disponibles, etc.
Construcción de modelos: Una forma
habitual y conveniente de analizar un sistema consiste en construir un
prototipo (un modelo material o conceptual) del mismo.
Validación del análisis: A fin de
comprobar que el análisis efectuado es correcto y evitar la posible propagación
de errores, en la fase de diseño es imprescindible proceder a la validación del
mismo. Para ello se verifica que:
·
El análisis debe ser
consistente y completo.
·
Si el análisis se
plantea como un paso previo para realizar un diseño, habrá que comprobar además
que los objetivos propuestos son correctos y realizables.
Modelación matemática
Un modelo matemático se define, de manera general, como
una formulación o una ecuación que expresa las características esenciales de un
sistema físico o de un proceso en términos matemáticos. [8]
Los modelos tienen dos propósitos básicos, con formas
fundamentales y de acuerdo con estos propósitos pueden ser:
a. Modelos dinámicos, tipo de ecuaciones generalmente diferenciales, para los estudios de control automático y
afines.
b. Modelos estáticos,
tipos de ecuaciones
generalmente
algebraicas, para estudios de diseño técnico y
optimización
técnico económica.
La forma y
uso
de los modelos también determinan indirectamente
los
límites de su tamaño físico en términos de número de variables
que se
estimen y la cantidad de ecuaciones implicadas, así como
el tamaño y la
complejidad de los medios físicos que se consideren.
La descripción cuantitativa de los sistemas de procesos, es una de las tareas de interés en la actualidad, para lograr este objetivo,
una de las condiciones previas, es
que la cantidad de información
disponible permita describir,
las
relaciones entre los elementos y
dentro de los elementos,
de manera que con el modelo obtenido de un sistema real, se pueda en determinada etapa del proceso
del conocimiento
sustituir al sistema real, y por medio de su
investigación y estudio
obtener la información deseada sobre el
sistema real, por ello, la calidad de un modelo matemático
está determinada por la precisión con que coincidan
los procesos en el
sistema real con los procesos obtenidos mediante el modelo, y debe
existir:
1. Concordancia objetiva con el propio sistema;
2. Posibilidad de sustituir el sistema en el proceso del
conocimiento;
3. Propiedad de suministrar información práctica sobre el sistema;
4. Determinadas reglas mediante las cuales la información del modelo pueda transformarse en información del
sistema.
Propiedades de los modelos
El estudio de los modelos como método fundamental del conocimiento debe servir para
conocer
las correlaciones
cuantitativas propias
de los fenómenos y con ello mejorar el sistema
para
direccionar él o los procesos como caso de estudio. Entonces la modelación es un método de manejo práctico
o teórico de un
sistema por medio del cual debe ser estudiado el sistema, pero no como tal sino por medio de un procedimiento auxiliar natural o artificial,
el
cual desde el punto de vista de los intereses planteados
concuerda con el sistema real que se estudia.
Dicho
sistema
en determinadas etapas del proceso del conocimiento, ser capaz de sustituir al real y por medio de su investigación y estudio, suministrar la información deseada sobre el
sistema real.
Entre las propiedades generales de los modelos se encuentran:
1. Los modelos
son representaciones
conscientemente
desarrolladas y simplificadas de una circunstancia. La construcción de modelos es una forma particular de la capacidad de abstracción del hombre.
2. Los modelos contienen las facetas esenciales y decisivas del proceso en dependencia del
fin del estudio.
3. Los modelos en general brindan nuevos conocimientos.
4. Los modelos se comprueban mediante
la
comparación de sus salidas con los
resultados de los
procesos reales.
5. Los modelos son sistemas de sustitución ya que sustituyen un original complejo para
aclarar
el
objeto de
investigación.
En resumen, puede plantearse que las tres
propiedades fundamentales de los modelos son la habilidad de abstracción como
operación mental para separar las propiedades de un objeto, habilidades de
semejanza como conjunto de características comunes para establecer su
naturaleza y habilidades de extrapolación de los resultados como aplicación de
un criterio lógico conocido de otros casos con el fin de extraer conclusiones o
hipótesis a futuro.
Clasificación de los modelos
Los modelos pueden clasificarse atendiendo a muchos factores, entre otras clasificaciones tenemos las siguientes:
1. De acuerdo a la teoría o técnica utilizada en su construcción, se clasifican en tres
tipos
de modelos y sus combinaciones:
a. Modelos de fenómenos de transporte. Basados en principios
físico químicos
b. Modelos de Balances de Población Aplicando los principios
de Balances de Población.
c. Modelos
Empíricos:
Su construcción
se basa en técnicas de ajuste de datos empíricos.
2. Desde el punto de vista de la naturaleza de las ecuaciones, se clasifican en pares opuestos como sigue:
a. Modelos determinísticos o estocásticos.
b. Modelos estacionarios o dinámicos.
c. Modelos
de parámetros combinados
o de parámetros distribuidos.
Otras clasificaciones de los modelos son dadas en la literatura, según los
aspectos de los objetos que el modelo refleja, a saber, modelos de estructuras, funcionales, de
comportamiento, combinados.
[9]
Confección, formulación y aplicación de
modelos en la industria
química y fermentativa
El planteamiento de un modelo matemático de un proceso exige, por
un lado el entendimiento del desarrollo del proceso y por otro, que la persona encargada del desarrollo del modelo posea capacidad de abstracción que le permita integrar por
medio
de formulación
matemática todas las peculiaridades del
objeto, debe además ser capaz
de despreciar los factores no influyentes y de simplificar
el modelo
en todo lo que sea
posible. [10]
Los modelos matemáticos de los equipos de un proceso, en conjunto dan forma al modelo matemático. Un modelo es la representación
matemática o grafica de la realidad que es utilizada para plantear un problema, normalmente de manera simplificada en términos relativos y planteados desde un punto de vista matemático, aunque también puede tratarse
de un modelo físico. [11]
Para llegar a
establecer
un modelo global, es necesarios iniciar con modelos
iniciales y que deben ser mejorados cada vez, para alcanzar un cierto
grado de éxito de un proceso e particular. El trabajado experimental
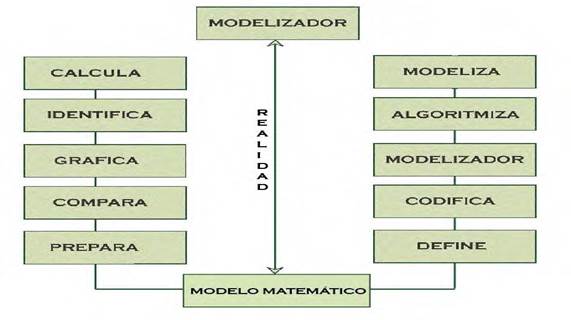
eficiente finaliza en un modelo matemático, apoyado en el método científico, que para establecerlo los investigadores deben considerar
la
guía que se representa en la
figura 1.
Fig. 1. Procedimiento a seguir para definir un modelo matemático.
Esta tarea, por su complejidad y requerimientos hace que las
exigencias en el modelo y su planteamiento sean elevados.
Los programas heurísticos (deductivos) juegan un papel fundamental en
el desarrollo
de una tarea de tal magnitud, ya que el fin de la confección
de dichos programas
es el obtener experiencias
metódicas para la estructuración
efectiva del trabajo creador del
hombre.
Si analizamos este aspecto encontramos en la confección de un
modelo matemático un movimiento de la contemplación,
al pensamiento abstracto y de ahí a lo concreto pensado (que no es otra
cosa que el modelo), como reflejo ideal del mundo real, lo que al comparar su adecuación completa se conoce como contemplación
viva. La modelación como parte de la Teoría de los Sistemas, está
relacionada
con
una serie de principios que son la base de los estudios posteriores
de la modelación. [12]
Etapas Generales
para el
Desarrollo de
modelos
Los pasos generales que llevan
a un modelo
matemático global
han sido relacionados por Kafarov
(1976) y
una
representación gráfica es la
Figura 2.
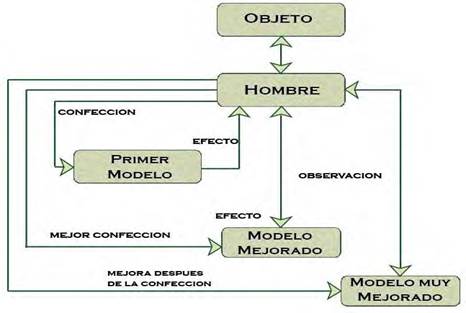
Fig. 2.
Representación gráfica para la mejora en la elaboración de un modelo. Fuente: [5]
La formulación de modelos debe ser un proceso progresivo, donde
inicialmente se formule un modelo de poca elaboración y luego se refine
gradualmente hasta obtener el equilibrio mencionado anteriormente.
Generalmente, es un error tratar de formular en el inicio del proceso el modelo
más complejo y elaborado.
La Modelación Matemática se lleva a cabo cumpliendo
los siguientes pasos: [13]
a) Identificación
del problema o proceso a resolver, junto con los objetivos, que deben ser
claros y concisos, con miras a obtener un resultado.
b) Conocimiento de los aspectos cognitivos que rigen el problema, por
medio de leyes, teorías y conceptos inmersos en la situación objeto de trabajo.
c) Formulación de la situación-problema en términos matemáticos
(matematización), mediante ecuaciones y/o relaciones matemáticas, identificando
para ello las variables, parámetros y los supuestos a que haya lugar.
d) Solución del problema y/o proceso matemático obtenido. Para ello se
hará uso de herramientas tales como tablas, gráficas, ecuaciones diferenciales,
estadística, investigación de operaciones.
e) Comparación del modelo con la situación real. En función de esto, es
necesario analizar los resultados obtenidos, verificando si las respuestas
alcanzadas son correctas, adecuadas o no, y además si se generan soluciones
extrañas.
f) Análisis de las restricciones al modelo. Es importante tener en
cuenta las suposiciones hechas, así como el marco donde se va a limitar el
dominio de la solución obtenida.
g) Escenario de aplicación del modelo, así como su interpretación. Es
aquí donde se evidencia el cumplimiento de metas, teniendo en cuenta sus
restricciones, si las hubiere.
La estrategia general
para
la elaboración
de modelos
sigue una trayectoria definida y razonable, la que aunque no
debe ser
aplicada mecánicamente pues las peculiaridades de
cada
sistema
dan
lugar a divergencias en el desarrollo de los métodos, se resume
en los siguientes pasos lógicos: [5]
Estudio preliminar:
Todo trabajo de modelación tiene
como
premisa
un estudio
preliminar en el cual se definan los problemas fundamentales para
el planteamiento del modelo. El primer
aspecto es reflejar los
objetivos que se persiguen con el modelo, es decir
los fines específicos del modelo.
Para la optimización deben decidirse los criterios deseados como parámetros de
optimización y además conocerse las relaciones fenomenológicas del proceso.
Es también necesario conocer sus limitaciones espaciales,
constructivas y de procedimiento. Las limitaciones espaciales las fijan las instalaciones
o equipos en los cuales el proceso se desarrolla y también las relaciones con los alrededores. Los constructivos están
determinados
por aspectos tales como: tipo de construcción, elementos de construcción, dimensiones de los equipos etc.
En este paso, se incluye el análisis crítico de la literatura y de
los modelos existentes para procesos análogos y debe terminar
con una corroboración
de los objetivos
propuestos y un
planteamiento de los modelos que pueden ser empleados en la
solución de la tarea.
Elaboración del modelo matemático detallado:
El modelo matemático de un proceso tecnológico debe describir en forma de relaciones
lógicas y/o matemáticas la totalidad de los procesos físicos químicos que ocurren en el sistema analizado, para
ello el estudio preliminar sirve como base y se podrán plantear las
consideraciones de
los procesos elementales esbozados en éste.
En el análisis de estos procesos elementales se combina
las consideraciones físicas
y físico químicas con Descripciones del tipo "Caja Negra".
En la elaboración de los modelos se comienza por
los elementos y para ello pueden aprovecharse los
modelos que en el estudio preliminar se hayan seleccionado o elaborado, después se acomete
el estudio de la modelación del proceso completo. El
modelo del proceso global se logra a través de la integración lógica y articulada de los modelos de los elementos y hasta ese momento tendrá un carácter teórico ya que los parámetros en incluidos no han
sido evaluados.
Los algoritmos
y formulaciones elaboradas
en esta
etapa, serán sometidos en las etapas posteriores
a una necesaria
comprobación que puede tener como resultado que este paso tenga que repetirse.
Fijación de los valores de los parámetros empíricos: [14]
En la modelación matemática de los procesos tecnológicos de la
industria química es problemático
la fijación de los parámetros
empíricos debido a la complejidad
de los procesos y los
cambios en las
corrientes másicas.
Por otro lado en
muchos casos
los valores obtenidos a nivel de laboratorio y planta piloto no son
extrapolables a escala industrial o solo lo
son en un rango limitado.
La obtención de estos parámetros empíricos puede hacerse partiendo
de valores establecidos, o determinándose a través de experimentos en equipos pilotos adecuados, o lo que es mucho mejor
en la misma
fábrica en dependencia de las posibilidades reales.
Los diseños de experimentos y los métodos estadísticos de
procesamiento de la información experimental y de los datos del control operacional industrial son un valioso
apoyo en la
determinación de los parámetros empíricos. Es importante además, la selección de los instrumentos de medida, su exactitud y error
relativo. Confección y puesta a punto
de los programa para
la computadora.
Para el desarrollo de modelos matemáticos, se hace necesaria la utilización de computadoras como herramienta para la realización
de los cálculos. Esto se logra por medio de un sistema de programas, que de una forma coordinada lleva a vías de hecho
la tarea
planteada.
Desarrollo de los cálculos numéricos con el modelo:
En esta etapa, el modelo pasa a ser el objetivo de estudio por medio del
cual se investiga el
comportamiento del proceso real, sin
necesidad de realizar costosas investigaciones obviando también la
influencia casual
de determinadas variables. Para ello es un
requerimiento que el modelo empleado sea adecuado
para la descripción del proceso tecnológico en los límites previamente establecidos.
Comprobación de la adecuación del modelo
matemático y
adaptación al proceso real.
La verificación de la adecuación del modelo permite determinar la concordancia de los resultados de este con los reales del proceso.
Para ello se comparan los resultados experimentales del proceso con
aquellos obtenidos por el modelo
partiendo de los mismos datos de
entrada. Esto permite determinar el grado de concordancia de los
resultados del modelo con los reales y si el modelo es capaz de reflejar adecuadamente el proceso para su estudio.
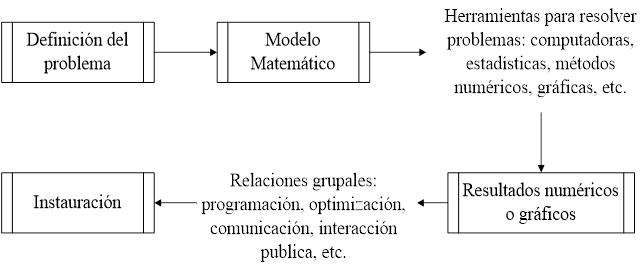
Este procedimiento para resolver problemas
ingenieriles a partir de modelos matemáticos se resumen en la Figura 3.
Fig. 3. Proceso
de solución de problemas de ingeniería. Fuente [8]
Optimización de los modelos a través de la Simulación
La obtención de modelos fiables puede requerir del
uso de algoritmos de optimización que permitan conocer los parámetros del
proceso a partir del modelo propuesto y los datos experimentales que se
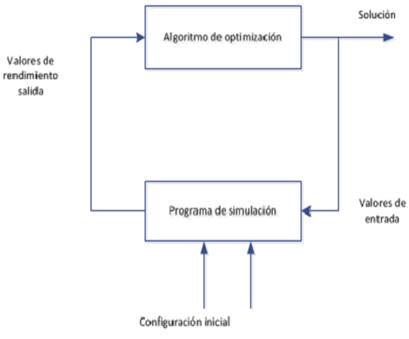
manejan. En la Figura 4 se puede observar el procedimiento para optimizar los
modelos matemáticos. [15]
Fig. 4.
Dinámica de optimización de modelos.
En la actualidad la modelación y simulación que desarrollan los
ingenieros tienen un soporte teórico imprescindible pero su implementación y
ejecución práctica se realiza usando aplicaciones informáticas. Es una
actividad indispensable cuando nos enfrentamos con el análisis y diseño de
sistemas multidisciplinares de cierta complejidad. El objetivo es ayudar o dar
el soporte necesario al diseñador durante el proceso de diseño, análisis y
diagnosis de sistemas ingenieriles. El software debe complementar el talento
del diseñador para que este pueda modelar y simular de forma lo más
eficientemente posible. El software hace posible establecer una valoración
final antes de que los sistemas sean construidos, y pueden aliviar la necesidad
de experimentos caros y dar soporte a todas las etapas de un proyecto desde el
diseño conceptual, pasando por el montaje hasta llegar a su funcionamiento.
Se puede establecer que estas aplicaciones informáticas pueden
clasificarse en los siguientes tipos: [6]
·
Matemáticas: Son
aquella donde se definen modelos matemáticos y se resuelven problemas de esta
ciencia (por ejemplo: resolver ecuaciones y sistemas de ecuaciones, cálculo de
derivadas e integrales, resolver ecuaciones diferenciales, etc.) dentro de los
que podemos mencionar con características generales el CurvExpert y el Derive
·
Ingenieriles: Estas
aplicaciones resuelven problemas ingenieriles usando métodos matemáticos. Su
característica más notoria es que los datos de entrada y las soluciones son los
del problema ingenieril. Generalmente el procesamiento matemático está dado en
segundo plano y es transparente para el usuario de la aplicación. Dentro de la
industria química podemos mencionar como los más usados el paquete de AspenPlus
y Hysys.
·
Mixtas: Se trata de
aplicaciones donde se presentan herramientas para la modelación y simulación
usando directamente los conceptos matemáticos pero también se presentan
modelaciones y simuladores que trabajan en el lenguaje y con conceptos
ingenieriles. Un ejemplo de estas aplicaciones es el MatLab.
Intensificación de procesos
Para lograr la intensificación de los procesos
tecnológicos de la industria química se utiliza el Análisis de Procesos, el
cual consiste en un amplio análisis científico-técnico y técnico-económico de
un proceso existente o concebido, en lo referente a las posibilidades de
realización óptima de los objetivos previstos, por ello constituye un elemento
importante para tomar decisiones más científicas y responsables.
El Análisis de Procesos sirve para descubrir las partes débiles en el
proceso de producción correspondientes y para la creación de medidas para su
eliminación parcial o completa lo que conduce a un aumento de su efectividad
permitiendo de esta forma un mejor aprovechamiento de las materias primas, la
energía y los medios de trabajo así como un aumento de los grados de eficiencia
de la fuerza de trabajo y el mejoramiento de las condiciones materiales bajo
las cuales ellos laboran. La intensificación de la producción mediante el
Análisis Complejo de Procesos, requiere la elaboración de objetivos económicos
en cada industria de forma concreta, entre lo que se encuentra
- Aumento de
la calidad y la cantidad de los productos elaborados.
- Disminución
de los consumos específicos y absolutos de materiales y energía.
- Mejoramiento
de las condiciones de trabajo.
- Ahorro de
fuerza de trabajo.
- Disminución
de la contaminación ambiental
Por consiguiente, la función clave de la intensificación de procesos es
su optimización, y como ya se ha visto anteriormente la optimización de
procesos se hace con apoyo de modelos matemáticos, elaborados a partir de los
valores reales del comportamiento de los propios procesos [16] y la
optimización de estos modelos se hace, en la mayoría de los casos debido a la
complejidad de estos, mediante la simulación.
Los modelos deben siempre considerarse como un soporte o ayuda para la
toma de decisiones y nunca como el reemplazo de las personas que toman las
decisiones. Si se formula un modelo pensando que sus resultados van a resolver
todos los problemas de decisión y van a ser implementados “a ojos cerrados,” se
cae en un grave error que puede traer consecuencias impredecibles. Existen en
la realidad muchos factores que no pueden ser involucrados en modelos
matemáticos y que sólo los grupos de personas que toman las decisiones pueden
evaluar. Por lo tanto, desde este punto de vista, los modelos son una poderosa
herramienta para este proceso, pero no el fin mismo de la decisión.
4. Conclusiones
Uno de los
aspectos básicos de la modelación matemática es el de considerar el suficiente
grado de abstracción de la realidad, de tal forma que el modelo tenga el
suficiente realismo, contra la posibilidad de que sea resuelto en un tiempo
de simulación aceptable. El arte de modelar consiste precisamente en
identificar las características fundamentales del sistema a ser involucradas en
el modelo y en diseñar modelos que permitan ser resueltos en forma eficiente.
Desde este punto de vista es tan importante y fundamental formular un modelo,
como encontrar sus soluciones en un tiempo computacional aceptable, para
después analizarlas e implementar las que se consideren mejores.
En la actualidad la intensificación de procesos está fuertemente ligada
a la modelación matemática y la simulación pues el avance en este campo de la
ciencia permite una mejor toma de decisiones y así un aumento en la calidad de
las industrias químicas.
5.
Referencias
[1] González, E (1991). Aplicación del Análisis
de Procesos en intensificación de distintas industrias de Cuba. Tesis de
disertación de Doctor en Ciencias. Universidad Central de Las Villas. Cuba.
[2] González
Suárez, E. W. F. Quezada Moreno, I. Y, González Herrera. D. N. Concepción
Toledo, Miño Valdés J.E. (2018). “Gestión del conocimiento para la industria
química y fermentativa con apoyo de la optimización” EdUNaM. ISBN:
978-950-766-133-4, Posadas 2018 González et al, 2018
[3] Klaus, G. (1974). Systrems Informationes
Strategien. V.E. H. verlag
Technik, Berlin.
[4] Orudzhev,
Z. M. (1974) La dialéctica como sistema. Editorial de Ciencias Sociales, Ciudad
de La Habana.
[5] Kafarov,
V. (1976). Cybernetic Methods in Chemistry and Chemical Engineering. MIR, Moscow, pp. 464-470. Moscú
[6] Legrá-Lobaina, A. A.
(2011). Modelación
Matemática y Simulación de Sistemas de Ingeniería. Monografía. Departamento de Matemáticas. Instituto
Superior Minero Metalúrgico de Moa
[7] Himmelblau, D.M. (1970). Process Analysis by Statistical Methods. New York,
John Wiley & Sons. EEUU.
[8] Chapra, S. C., & Canale, R. P. (2011). Capítulo 1: Modelos matemáticos y solución de
problemas de ingeniería. En Métodos numéricos para ingenieros. Sexta edición.
Mc. Graw-Hill., pp. 10-15, ISBN 978-607-315-0499-0499. México
[9] Vidal-Holguín, C. J. (2011). Introducción a la modelación matemática y
optimización., Programación lineal, Programación No Lineal y Teoría de Redes:
Formulación y solución de modelos, teoría de dualidad, análisis de
sensibilidad, problema del transporte y problemas seleccionados de redes. Cali:
Universidad del Valle, Escuela de Ingeniería Industrial y Estadística.
[10] Duran Guillermo
(2006). Investigación de operaciones, modelos matemáticos y optimización.
Seminario JUNAEB-DII. Enero de 2006. Universidad de Chile.
[11] Yois, S., y Pascuas, R. (2008). Modelamiento matemático aplicado al
modelamiento espacial. Revista Sociedad de la Información. Art. N°4. Bogotá,
Colombia.
[12] González-Suárez, E., Quezada-Moreno, W., Peralta-Suárez, L. M., &
Concepción-Toledo, D. N. (2016). Modelación y optimización de procesos: impacto
científico en la Industria Química y Fermentativa. Ecuador: Editorial UTC.
[13] Brito, M., Alemán, I., Fraga, E., Para, J. y Arias, R. (2011). Papel de
la modelación matemática en la formación de ingenieros. Ingeniería Mecánica, 14(2), pp.
129-139.
[14] Rudd,
D.F.; C.C. Watson (1968): Strategy of Process
Engineering. Mc GrawHill. New
York
[15] Torregrosa López, J. (2016). Conceptos básicos del modelado de procesos.
Valencia: Universidad politécnica de Valencia. Departamento de Ingeniería
Química y Nuclear.
[16] Plaza Gálvez, L.F. (2017). Modelación matemática en ingeniería. Revista de
Investigación Educativa de la Rediech 7(13), pp. 47-57. Colombia