Elsevier instructions for the preparation of a 2-column-format camera ready paper

1. Introducción

Los cojinetes magnéticos se han comenzado a emplear en diversas aplicaciones donde es necesario utilizar motores de altas velocidades, debido a que los sistemas con rodamientos generan fricciones que limitan la velocidad final. Dichas fricciones van acompañadas de desgastes mecánicos y elevadas temperaturas [1].

Los cojinetes magnéticos son rodamientos que sostienen a la carga utilizando fuerzas magnéticas. Existen diferentes tipos de rodamientos magnéticos [2], entre ellos se pueden discriminar dos grupos bien definidos, los cojinetes pasivos y los activos; los primeros utilizan imanes permanentes para generar las fuerzas, pero son difíciles de diseñar; mientras que los segundos funcionan utilizando electroimanes, es decir, bobinas excitadas por una corriente eléctrica que genera las fuerzas para equilibrar la carga en una determinada posición. Por otro lado, existen cojinetes híbridos que emplean imanes permanentes para generar una situación de equilibrio estático y a través de los electroimanes se generan las fuerzas necesarias para mantener el equilibrio dinámico.

Dentro de los cojinetes activos se pueden emplear diferentes topologías para realizar el control, entre ellas la topología homopolar, que consiste en un arreglo de 4 electroimanes, donde cada uno permite el movimiento en un sentido de los ejes XY. Mientras que la otra topología empleada es el heteropolar, el cual está compuesto de 8 bobinas, donde se conectan de a pares para realizar el control de los diferentes sentidos de los ejes XY [3]. Un tercer grupo son los tripolares, los cuales son poco frecuentes en la literatura [4].

Los sistemas rotacionales que emplean este tipo de rodamientos pueden poseer varios grados de libertad, es decir, pueden levitar totalmente utilizando dos cojinetes radiales y un axial o únicamente emplear un cojinete radial apoyado sobre un rodamiento mecánico especial para alta velocidades.

El objetivo de este trabajo es plantear, diseñar e implementar un control en lazo cerrado para un cojinete radial activo para un motor del tipo brushless que opera a 20000 RPM.

En la sección II se presentan el desarrollo teórico del cojinete magnético radial, junto con el diseño de los controladores a implementar. En la sección III se presentan el prototipo, los controladores y los resultados de la implementación; finalmente se describen las conclusiones y trabajos a futuro.

2. Desarrollo

2.1. Modelo del cojinete radial

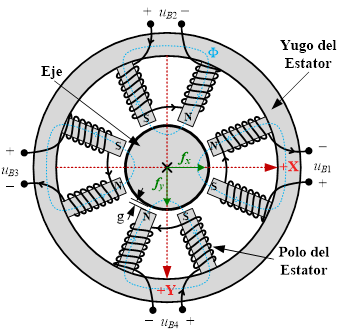
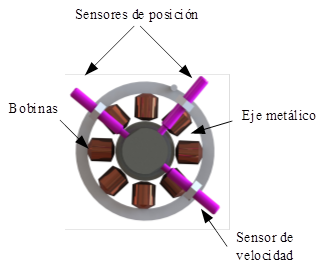
El rodamiento magnético diseñado y construido consiste en un cojinete heteropolar, constituido por un conjunto de bobinas como se muestra en la Fig. 1. En el centro se encuentra un eje metálico, y alrededor un estator conformado por el yugo y los 8 polos, en cada polo se montan bobinas de un número determinado de espiras. Existe una distancia entre los polos y el eje denominado gap (g). Dicha distancia será el limite donde se podrá mover el eje, en general esta distancia no supera el orden de los milímetros (g < 2mm). Como se observa en la misma figura, las bobinas son interconectadas de a pares con la configuración NNSSNNSS (N: Norte – S: Sur). Existen 4 pares de bobinas por las cuales circula una determinada corriente, dicha corriente generan campos magnéticos que producen fuerzas de atracción hacia los diferentes cuadrantes. El par de bobina identificado como u_B₁ genera una fuerza hacia el denominado eje +X, en cambio u_B₃ genera una fuerza hacia –X; de la misma manera u_B₄ y u_B₂ generan fuerzas sobre el eje Y.

Fig. 1. Esquema fundamental del cojinete magnético.

El funcionamiento de los cojinetes magnéticos activos parte de establecer una corriente media en todas las bobinas [5], denominada corriente de bias I_b, que genera un equilibrio estático de fuerzas sobre el eje metálico. Para realizar el control de la posición del eje se utiliza una corriente i_b de manera que la corriente total sobre la bobina está definida como I_b+i_b. Para realizar un desplazamiento en uno de los ejes, se incrementa el valor de la corriente en +i_b en un par de bobina y se disminuye en este mismo valor ‒i_b al par opuesto. De la misma manera se generaría un desplazamiento en el eje ortogonal. Al definir la corriente de bias se establecen el máximo y el mínimo posibles para el control de las corrientes, de manera que el mínimo será I_b – I_b = 0A, mientras que el máximo será I_b + I_b = 2 I_b. Cabe aclarar que el objetivo de los cojinetes es mantener la pieza metálica en el centro geométrico del cojinete.

Los sistemas de éste tipo son inestables y no lineales debido a las dinámicas involucradas. Por lo tanto, es necesario realizar un control de las posiciones a través de un lazo cerrado, de ésta manera a través de un sensor de posición se mide la ubicación del rotor en un eje y a partir de dicha información se ajusta la corriente para corregir la ubicación de dicho eje mediante los electroimanes.

Para obtener un modelo lineal se realizan diferentes consideraciones, donde la principal consiste en permitir desplazamientos pequeños en torno del punto de equilibrio o centro geométrico; aun así, la fuerza generada por el sistema es no lineal y dependiente del cuadrado de la corriente que circula por la bobina e inversamente proporcional al cuadrado del desplazamiento [1][5].

Para definir el modelo de los rodamientos magnéticos se establecen las ecuaciones matemáticas que describen el sistema eléctrico y el sistema mecánico. Basado en [6] y tomando la consideración del párrafo anterior, se obtiene la siguiente expresión linealizada en torno a centro geométrico del cojinete, que también es válida para el eje transversal.

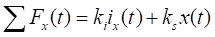
(1)

donde i_x es la corriente de control de las bobinas en la dirección x; mientras que k_i es la constante de fuerza-corriente y k_s es la constante de fuerza-desplazamiento, definidas como:

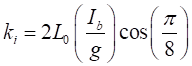
	(2)
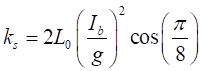
	(3)

donde I_b es la corriente de bias de las bobinas, g es el gap, dado por la diferencia entre el radio del rotor y el radio interno entre el centro geométrico y el polo del yugo de la bobina. L₀ la inductancia del bobinado en la posición central del eje establecido como

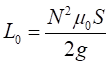
(4)

Dicha expresión depende del número de espiras N de las 2 bobinas en serie, de la permeabilidad del aire µ₀ y del área S de un polo del estator.

A partir de la Fig. 1, aplicando los conceptos de la ley de Newton se establece la siguiente ecuación [7] de movimiento en uno de los ejes:

	(5)

donde m es la masa del rotor.

Además se toma la dinámica del sistema eléctrico como se describe en [8] definido como

(6)

donde r_L y L₀ son la resistencia e inductancia del bobinado, mientras que u_x(t) es la tensión de control del sistema. El factor k_i es la constante de fuerza corriente que genera una fem en el inductor debido al desplazamiento del eje, dicho factor se considera despreciable respecto a los otros términos [7].

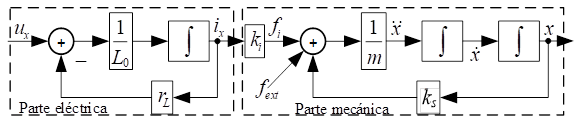
El sistema para un eje queda representado por el diagrama en bloques de la Fig. 2.

Fig. 2. Diagrama de bloques del sistema dinámico de un cojinete magnético radial para un solo eje.

Donde f_ext es un disturbio, que en este caso está representando la fuerza de desbalance que posee el eje al girar. Dicha fuerza es proporcional al cuadrado de la velocidad de giro por la masa de desbalance y la distancia de dicha masa del baricentro del eje.

2.2. Esquema de control propuesto

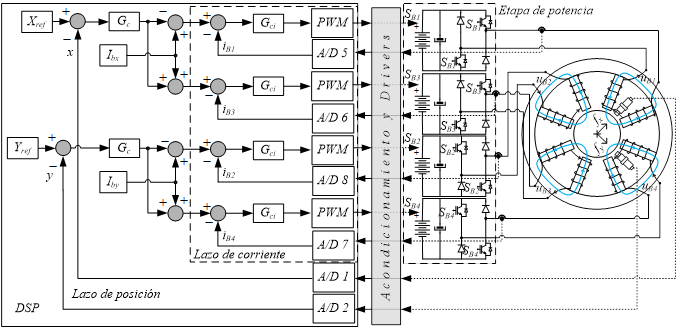
Para realizar el control se proponen dos controladores, un control de corriente interno, definido para controlar la dinámica dado por la expresión (6); y un control de posición externo para controlar la dinámica presentada en la ecuación (5). El esquema general se presenta en la Fig. 3, donde se esquematiza además la ubicación de los sensores, tanto de corriente como de posición, las etapas de potencia junto a los drivers y las entradas analógicas digitales (ADC) y salidas de modulación por ancho de pulso (PWM) del procesador digital de señales (DSP).

Para realizar el control de corriente, y en consecuencia el control de la posición, se emplea una etapa de potencia dado por un convertidor de corriente continua-corriente continua (CC-CC) que se presenta en el esquema de la Fig. 3. Dicho convertidor tiene la capacidad de generar una circulación de corriente en un solo sentido, con lo cual se genera la corriente de bias I_b y luego se establecen montada sobre la misma las corrientes necesarias para el control del cojinete [9][10]. En este caso son necesarios cuatro convertidores de este tipo, que proporcionan las corrientes para manejar los cuatro cuadrantes de movimiento del rodamiento magnético radial.

Fig. 3. Esquema de control con lazo interno de corriente y lazo externo de posición.

2.2.1. Lazo interno de corriente

El lazo de corriente que se propone es del tipo proporcional integral (PI), teniendo en cuenta en el diseño que la respuesta de corriente sea más rápida que la respuesta de posición, de manera que puede ser despreciada y así definir que el control de posición es una relación entre una corriente y la posición del cojinete. Realizando dicha suposición se puede considerar que la corriente de referencia del lazo de corriente es igual a la corriente sobre el par de bobinas.

2.2.2. Lazo externo de posición

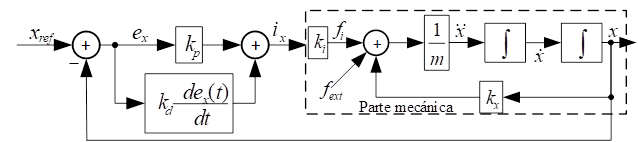
El lazo de control de posición se determina utilizando la dinámica de la ecuación (5), y el controlador propuesto es del tipo proporcional derivativo (PD), el cual se emplea para estabilizar el sistema, como primera medida. Además, se considera despreciable la dinámica del lazo de corriente, ya que responde con una velocidad mucho mayor que la posición. Por lo tanto, podemos el sistema en lazo cerrado de posición está definido como se muestra en el siguiente esquema:

Fig. 4. Esquema de control de posición.

Teniendo en cuenta que la referencia de posición es nula, se puede establecer que e_x(t) = –x(t) y la corriente de control es

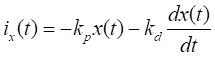
(7)

Con la expresión 7 y 5 se llega a que

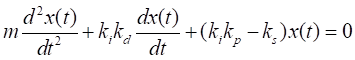
(8)

Resultando similar a un sistema masa-resorte, donde la ganancia k_ik_d es la constante de fricción viscosa (amortiguamiento) y (k_ik_p – k_s) es la constante del resorte (rigidez). Para que el sistema sea estable tanto la constante de rigidez como la de amortiguamiento deben ser positivos.

Empleando la dinámica observada en la ec (8) y lo establecido en [7] se definen algunos criterios para seleccionar los valores de las ganancias del compensador de manera que

(9)

donde k es una constante que define la rigidez del movimiento y d establece el amortiguamiento.

La constante k debe estar comprendido entre 1 a 3 veces el valor de k_s para proporcionar una rigidez intermedia, dicho valor depende de la aplicación que se quiere emplear y de los disturbios externos que se puedan presentar a la hora de implementar el sistema. Por otro lado establece que el coeficiente d debe estar definido entre

(10)

El sistema de control planteado permite estabilizar el sistema pero no permite obtener error de posición nulo, con lo cual se incluye un controlador integral, de manera que la ganancia vinculada a ésta acción sea aproximada al valor de la ganancia proporcional. Por lo tanto el controlador empleado es

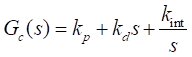
(11)

donde k_p es la ganancia proporcional, k_d la ganancia derivativa e k_int la integral.

El controlador planteado es de tiempo continuo, el cual debe ser discretizado para ser empleado en un DSP.

3. Resultados

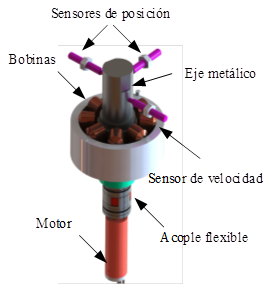
Para la implementación del rodamiento magnético se construye el prototipo que se presenta en la Fig. 5, mientras que en la Tabla 1 se presentan algunas de las características constructivas, debido a tratados de confidencialidad no se detallan en su totalidad dichos prametros.


a) Modelo vista lateral	b) Modelo vista superior

Fig. 5. Modelo diseñado y construido de los rodamientos magnéticos.

Tabla 1: Datos del prototipo empleado.

Característica	Datos
Masa del rotor m	0,660 kg
Longitud del rotor	0,104 m
Radio rotor r	0,0225 m
Velocidad nominal ω_r	20000 rpm
Corriente de bias I_b	1 A
Resistencia serie del bobinado r_L	1,375 Ω
Tensión Entrada V_cc	36 V
Frecuencia de muestreo f_m	20 kHz

Uno de los puntos más importantes para la implementación de este tipo de sistemas es la frecuencia de muestreo, dicho valor está dado por la máxima dinámica que se tiene en el sistema. En este caso la dinámica está vinculada con el disturbio, y dicha perturbación está enlazado con la velocidad de giro, con lo cual si se quiere llevar al motor a una velocidad de 333,3 Hz, es necesario adquirir dicha señal con una buena representación. Un criterio es seleccionar una frecuencia de muestreo de al menos 10 veces la frecuencia máxima. Para este caso se opta por adquirir las señales a una frecuencia de 20 kHz.

Por otro lado, el ancho de banda de los sensores utilizados en ésta aplicación deben permitir realizar el seguimiento de las dinámicas sin incorporar atenuaciones o ruidos indeseables. Por éste motivo se utilizaron sensores de corriente del tipo LEM LA 25-NP que posee un ancho de banda de 150 kHz. Mientras que los sensores de posición son los 3300 XL NSv de Bentley Nevada, los cuales poseen un ancho de banda de 10kHz. La señal proporcionada por el sensor de posición poseen offset de 2,8V; además el máximo movimiento de +0,4mm corresponde a 4,5V; mientras que el mínimo de –0,4mm equivale a 0,5V. Obteniendo una ganancia de 0,8mm/4V menos el offset.

Los actuadores de la etapa de potencia disponibles para implementación inmediata son llaves del IGBT, disparadas por sus correspondientes drivers, los cuales son manejados por una etapa amplificadora, que sirve de interfaz con el DSP. De la misma manera, los sensores son acondicionados para ser adquiridas las señales por el conversor analógico digital (ADC).

3.1. Desempeño del control interno de corriente

El controlador de corriente utilizado es un PI, donde la función de transferencia en tiempo continuo empleada se muestra a continuación

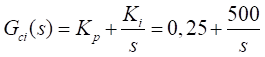
(12)

Utilizando la aproximación de la diferenciación dada por el operador de Laplace S, empleando el método de la derivada hacia atrás en tiempo discreto de Backward Euler, con el periodo de muestreo (T = 1/f_m) de la Tabla 1 se llega a

(13)

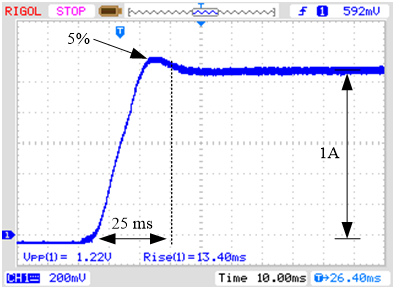
Mediante la implementación en el DSP se observa en la Fig. 6 que la respuesta a un escalón de corriente unitario posee un tiempo de establecimiento es de 20 ms y un sobrepaso de 5%.

Fig. 6. Respuesta experimental del lazo interno de corriente para una referencia en escalón de 1A. Esc: 1 A/V.

3.2. Desempeño del control externo de posición

Como se describió en la sección 2.2.2 los lazos de posición son controlados por una acción PID. De acuerdo con (9) y (10) se establece que la constante de rigidez k será de 2,6 veces k_s y que la constante de amortiguamiento d será de 0,64 veces el valor de 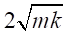. Mientras que el valor de la constante integral se define aproximadamente igual a k_p. Por lo tanto, el controlador PID en tiempo continuo será

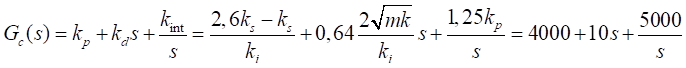
(14)

De la misma manera que en (13), mediante la discretización de Backward se obtiene:

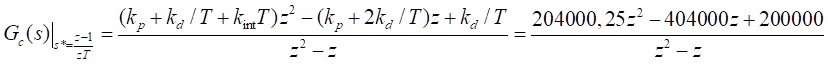
(15)

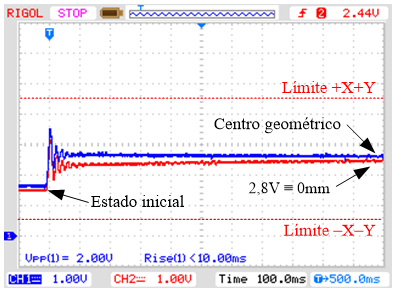
Para verificar el correcto funcionamiento del lazo externo de posición se implementa el controlador diseñado en el DSP; las respuestas a un escalón desde la posición actual al centro geométrico del cojinete (0mm; 0mm) se presentan en la Fig. 7. En dicha figura se observa la dinámica transitoria de ambos ejes, de manera que se inicia en –0,24mm (1,6V), se produce un sobrepaso y llegan a régimen permanente en 100ms. El valor final constante de 2,8V equivale al centro geométrico del rotor y se corresponde con la posición 0mm en x y 0mm en y.

Por otro lado se realizan algunos ensayos para observar la dinámica de corriente y la de posición en cada par de bobinas cuando se colocan las referencias de posición a cero. Estas respuestas transitorias se presentan en las Fig. 8 a, b y Fig. 9 a y b.

Fig. 7. Respuesta experimental del lazo de posición de ambos ejes para una referencia en escalón de 0 mm. Esc: 0,8mm/4V. Offset 2,8V.


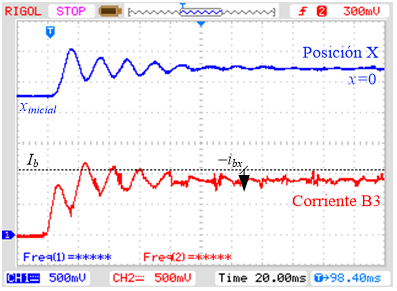
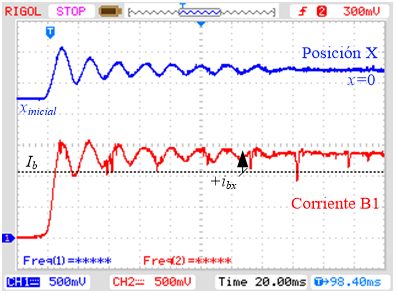
a) Posición X – Corriente en B3.	b) Posición X – Corriente en B1.
Fig. 8. Dinámica experimental del sistema en el eje X junto a la acción de las corrientes. Esc X: 0,5mm/4V; Esc. I: 1A/V.

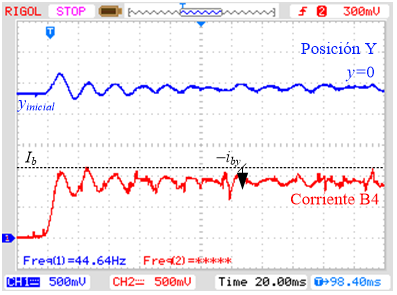
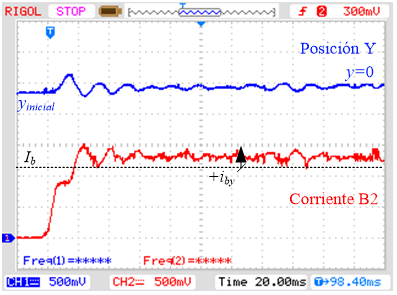
Al evaluar la dinámica de las corrientes se observa que existe una corriente de bias de 1A y sobre ésta se suma o se resta la acción de control del lazo externo de posición. En el caso de los pares de bobinas B3 y B4 (Fig. 8 a y Fig. 9 a) se observa que la corriente está por debajo de I_b, mientras que los casos B1 y B2 están por encima (Fig. 8 b y Fig. 9 b). De manera que el par de bobinas con menor corriente ejerce una fuerza menor que su contraposición con lo cual mantiene la masa en un punto tal que centra el rotor.


a) Posición Y – Corriente en B4.	b) Posición Y – Corriente en B2.

Fig. 9. Dinámica experimental en el eje Y junto a la acción de las corrientes. Esc Y: 0,5mm/4V; Esc. I: 1A/V.

3.3. Órbitas XY

De la manera que se presentó en el apartado anterior se confirma el correcto funcionamiento del cojinete magnético en una posición estática del eje del motor. A continuación se realizaron diferentes pruebas de giro del rotor y se obtuvieron los desempeños ante este tipo de perturbación. Para ello se empleó un motor brushless Maxon EC 25 de velocidad nominal de 62000 rpm/250W, con su correspondiente servocontroladora ESCON 70/10.

Los ensayos realizados consistieron en tomar con el osciloscopio las órbitas generadas por el cojinete ante las perturbaciones generadas por el giro; dichas perturbaciones son el resultado de las excentricidades y los desbalances que posee el eje en rotación. Las curvas de aceleración son constantes hasta alcanzar la velocidad del ensayo.

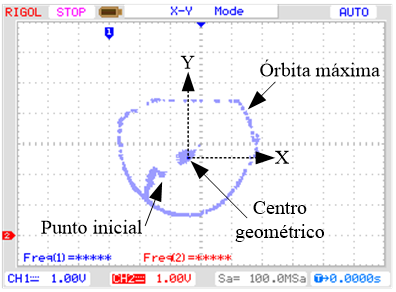
La Fig. 10 muestra la órbita máxima admitida por el cojinete, el punto inicial y la posición final cuando el motor no está girando. Se observa que el eje permanece en el centro con pequeños movimientos de un máximo de 0,0625 mm.

Fig. 10. Órbita a 0 rpm para una referencia en escalón de 0 mm. Esc: 0,8mm/4V.

Luego, cuando existen diferentes velocidades, dichas órbitas alrededor del punto central se van incrementando debido a las fuerzas que ejercen las masas desbalanceadas del eje. Cabe recordar que las fuerzas de desbalance sobre el eje son proporcionales al cuadrado de la velocidad de giro. En las siguientes figuras se presentan, por un lado, las órbitas del cojinete desde el arranque hasta una determinada velocidad de prueba, y por otro, la máxima órbita en la velocidad de prueba.

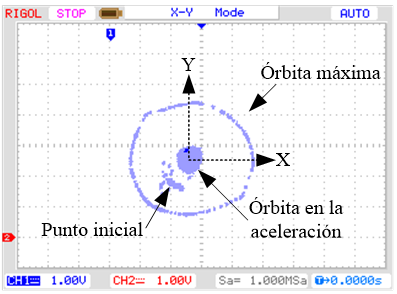
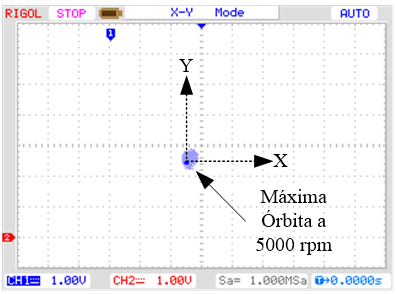
En la Fig. 11 a y b se observa que la órbita máxima se da en el transitorio y llega a 0,1 mm, Mientras que en régimen a 5000 rpm la órbita se mantiene en 0,06 mm.


a) Transitorio de aceleración.	b) Velocidad permanente a 5000 rpm

Fig. 11. Órbita a 5000 rpm para una referencia en escalón de 0 mm. Esc: 0,5mm/4V.

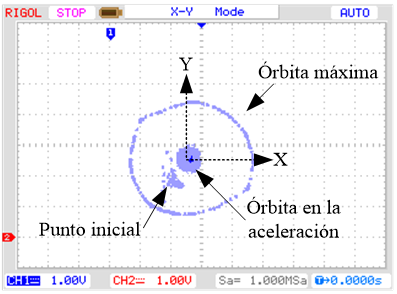
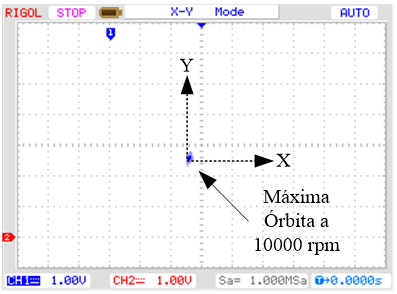
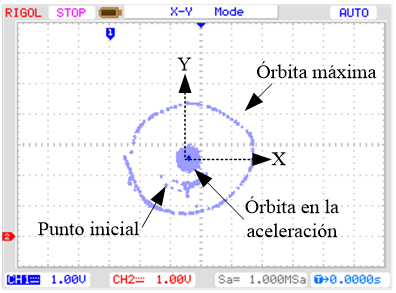
En la Fig. 12 y Fig. 13 la órbita en los transitorios se mantiene en aproximadamente 0,1 mm y en las velocidades del ensayo se mantienen 0,04 mm aproximadamente.


a) Transitorio de aceleración.	b) Velocidad permanente a 10000 rpm

Fig. 12. Órbita a 10000 rpm para una referencia en escalón de 0 mm. Esc: 0,5mm/4V.


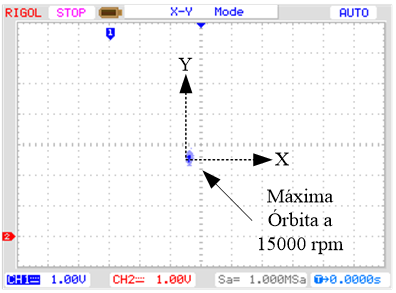
a) Transitorio de aceleración.	b) Velocidad permanente a 15000 rpm

Fig. 13. Órbita a 15000 rpm para una referencia en escalón de 0 mm. Esc: 0,5mm/4V.

3.4. Revoluciones XYt

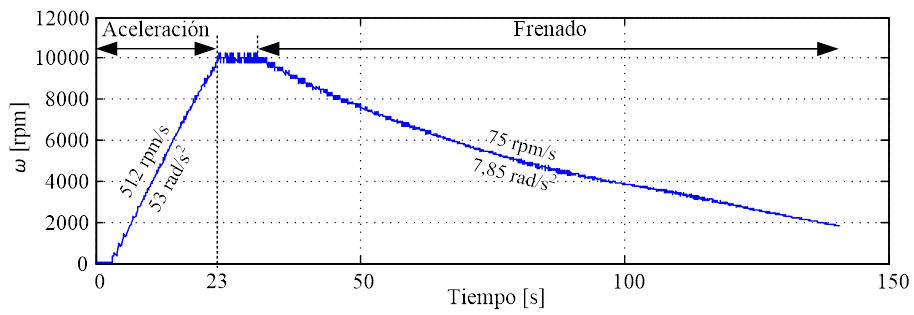
Finalmente se realiza un ensayo donde se releva las posiciones XY y tiempo, donde se realiza un ensayo de aceleración constante hasta la velocidad de 10000 rpm aproximadamente y luego se libera el motor para que se frene naturalmente. Dicho perfil de velocidad se presenta en la Fig. 14.

Fig. 14. Perfil de velocidad empleado para el ensayo de revoluciones.

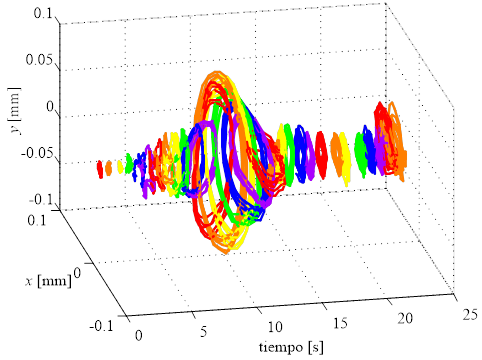
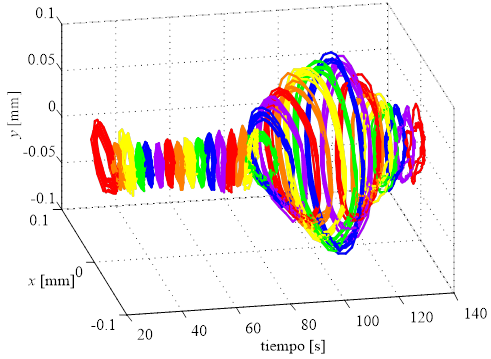
En la Fig. 15 a se presentan las órbitas en función del tiempo para cuando la maquina se acelera y en la Fig. 15 b para cuando se frena.


a) Órbitas cuando se acelera el motor.	b) Órbitas al frenar el motor.

Fig. 15. Curvas XYt para una rampa de aceleración y frenado constante.

En ambas curvas se observa que existen órbitas mayores, al buscar el punto se observa que en ambos casos se corresponde con la velocidad 3571 rpm = 59,51Hz. Dicho punto es una frecuencia de resonancia del eje. A pesar de dicha resonancia las órbitas no superar el valor de 0,1 mm.

4. Conclusiones

El trabajo describe una estrategia de control para un cojinete magnético radial activo; inicialmente se presentó el modelo del cojinete magnético radial activo empleado en ésta situación, luego a partir de dicho modelo se propuso los parámetros para el control. Las técnicas de control empleadas fueron un control interno PI de corriente y un control externo de posición del tipo PID. Los diseños realizados en tiempo continuo fueron discretizados e implementados en un DSP. Con diferentes resultados se pudo verificar el diseño y se comprobó el correcto funcionamiento para el rango de velocidades establecidas.

Como trabajos futuros se desea incluir un controlador feedforward, de manera que se oponga a las perturbaciones que genera el desbalance de masa del eje rígido empleado en el cojinete. Además se prevé implementar técnicas de control no lineal a fin de comprobar el rechazo a perturbaciones.

Agradecimientos

Este trabajo ha sido presentado de manera preliminar en la 8va Jornada de Investigación, Desarrollo Tecnológico, Extensión, Vinculación y Muestra (JIDeTEV 2018) [11] llevado a cabo en el mes de agosto del 2018 en la Facultad de Ingeniería de la Universidad Nacional de Misiones.

Referencias

[1]	M. Puskaric, Z. Car, y N. Bulic, “Magnetic Bearing Control System based on PI and PID Controllers,” Teh. Vjesn. - Tech. Gaz., vol. 25, no. 1, pp. 136-140, feb. 2018, 10.17559/TV-20160726112308.
[2]	T. Nussbaumer, P. Karutz, F. Zurcher, y J. W. Kolar, “Magnetically Levitated Slice Motors - An Overview,” IEEE Trans. Ind. Appl., vol. 47, no. 2, pp. 754-766, March/April 2011, 10.1109/TIA.2010.2102731 .
[3]	Weiyu Zhang, Huangqiu Zhu, “Radial magnetic bearings: An overview,” Results in Physics, vol. 7, pp. 3756-3766, August 2017, 10.1016/j.rinp.2017.08.043.
[4]	Meeker, D.C.; Maslen, E.H. “Analysis and control of a three pole radial magnetic bearing,” In Proceedings of the Tenth International Symposium on Magnetic Bearings, Martigny, Switzerland, August 2006.
[5]	J. Denk, D. Stoiber, H. Kopken and H. Walter, "Industrialization of AMB Systems With Standard Drive Technology," IEEE Transactions on Industry Applications, vol. 49, no. 2, pp. 791-798, March-April 2013, 10.1109/TIA.2013.2242426
[6]	A. Chiba, T. Fukao, O. Ichikawa, M. Oshima, M. Takemoto, y D. G. Dorrell, “Magnetic Bearings and Bearingless Drives”. Elsevier Science, 2005.
[7]	G. Schweitzer y E. H. Maslen, “Magnetic bearings : theory, design, and application to rotating machinery”. Springer, 2009.
[8]	R. RARICK, “Control Of An Active Magnetic Bearing With And Without Position Sensing,” M.S. thesis, Department of Electrical and Computer Engineering, Cleveland State University, Ohio, USA, 2007.
[9]	T. E. Seiphetlho, “Power electronic activation for active magnetic bearings,” M.S. thesis, Department of Electrical, Electronic and Computer Engineering, North-West University, Potchefstroom Campus, South Africa, 2006.
[10]	Zhu Changsheng and Mao Zhiwei, “A PWM Based Switching Power Amplifier for Active Magnetic Bearings,” in International Conference on Electrical Machines and Systems, Nanjing, China, 2005, pp. 1563-1568, 10.1109/ICEMS.2005.202812
[11]	G. Y. Aguirre, L. A. Urbani, M. J. Kelm, D. A. Kelm, M. E. Yasnikowski, “Cojinete Magnéticos empleados en motores de alta velocidad,” 8va Jornadas de Investigación, Desarrollo Tecnológico, Extensión y Vinculación, FI, UNaM, Oberá, Misiones, Agosto 2018, ISSN 2591-4219 http://conferencias.fio.unam.edu.ar/index.php/JIDeTEV/Octava-JIDeTEV/schedConf/presentations