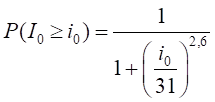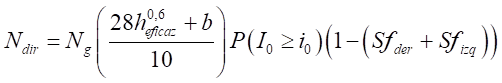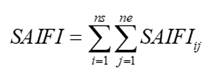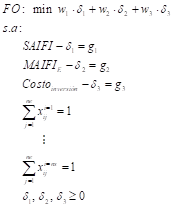Elsevier instructions for the preparation of a 2-column-format camera ready paper

1. Introducción

Las descargas atmosféricas son una de las principales causas de faltas y averías en sistemas de distribución de energía eléctrica (SDEE). Las descargas atmosféricas pueden ser por impacto directo en el alimentador o por descargas indirectas en las vecindades de los alimentadores, ambas producen sobretensiones críticas y pueden causar interrupciones momentáneas o permanentes [1], [2]. El cálculo de este tipo de sobretensiones se realiza ante muchas incertidumbres, dada la naturaleza aleatoria del rayo y el conocimiento impreciso de sus principales parámetros [3].

Actualmente, la red brasileña tuvo diferentes problemas relacionados con interrupciones por descargas atmosféricas [4], [5] y considerando que en la región sudamericana posee una alta incidencia de las descargas atmosféricas en comparación con cualquier otro lugar en el mundo [6], [7]. Por décadas, las concesionarias de energía eléctrica del mundo entero han trabajado en la mejora de la Calidad de la Energía Eléctrica suministrada a sus consumidores [8]. Una creciente preocupación de estas empresas, y tema de gran interés de la sociedad, es la interacción entre el fenómeno de la descarga atmosférica y los SDEE. Se busca, en este asunto, el desarrollo y mejora del SPDA debido a los efectos indeseables de las descargas atmosféricas. La creciente preocupación por parte de las Concesionarias en mejorar el sistema de protección, así como los índices de Calidad de la Energía Eléctrica de los Sistemas Eléctricos de Potencia (SEP) ante la interacción con las descargas atmosféricas, hizo estos asuntos un gran desafío en el ambiente académico.

Las faltas en el sistema eléctrico, debido a las descargas atmosféricas, producen una degradación de los indicadores de la calidad de servicio de distribución de energía eléctrica, definidos por los Procedimientos de Distribución de Energía Eléctrica en el Sistema Eléctrico Nacional (PRODIST) de la Agencia Nacional de Energía Eléctrica (ANEEL) [9]. Los disturbios de la Calidad de la Energía Eléctrica causan la insatisfacción de los consumidores y grandes pérdidas económicas para las compañías eléctricas y para la sociedad. Se estima que las descargas atmosféricas producen el 70% de las interrupciones en las líneas de transmisión y del 30% al 60% de los apagones en las redes de distribución [10].

En regiones con alta densidad de descargas atmosféricas, la principal práctica de protección para evitar que se produzcan fallas en el SDEE consiste en la colocación de cable de blindaje o cable de guardia sobre los conductores de las fases [2]. Algunas empresas distribuidoras colocan captor Franklin y/o descargador para-rayos en los postes cercanos donde existen transformadores de distribución. El cable de blindaje y el captor Franklin se conectan eléctricamente a través de las estructuras con cable de bajada a los sistemas de puesta a tierra (PAT). De esta forma, direccionan hacia el suelo las corrientes de eventuales sobretensiones producidas por descargas directas o sobretensiones inducidas por descargas indirectas cercanas a los alimentadores. Actualmente, estas metodologías son utilizadas por las Concesionarias para mejorar la confiabilidad del sistema y obteniendo así beneficios técnicos y económicos [11] - [16].

Las Concesionarias de Energía Eléctrica aprovechan su experiencia pasada, datos históricos de confiabilidad y otras consideraciones técnicas para seleccionar el tipo de estructura y sistema de PAT considerando el sistema de protección existente (interruptores, reconectadores y fusibles).

Los métodos de optimización matemática, como la programación lineal de entera mixta (PLIMM), demostraron alcanzar la solución ideal global en un número finito de etapas [17]. Por lo tanto, en este trabajo, se presenta un nuevo modelo basado en PLIMM, optimización de indicadores de confiabilidad SAIFI y MAIFI_E. El modelo propuesto considera las interrupciones momentáneas y permanentes, así como el número de clientes afectados en una estrategia de proyecto de SPDA al aprovechar los costos inherentes a la solución. La solución óptima del modelo se encuentra usando solvers comerciales que garantizan la solución óptima global para modelos PLIM [17]. Para evaluar el modelo de optimización propuesto se utiliza un sistema de prueba formado por 3 secciones de líneas de un alimentador real. Los resultados de las pruebas muestran la viabilidad y la generalidad del modelo de optimización propuesto.

El resto de este artículo está organizado de la siguiente manera. La sección 2 trata sobre el cálculo de la tasa de faltas por descargas atmosféricas. En la sección 3 se describe la metodología utilizada. En la sección 4 se muestra el modelo para optimizar los indicadores de confiabilidad del sistema utilizando PLIMM. El estudio de caso y los resultados se presentan en la sección 5. En la sección 6 se describen las conclusiones.

2. Cálculo de la Tasa de Faltas por Descargas Atmosféricas

Los trabajos pioneros en el cálculo de la tasa de faltas en líneas aéreas fueron desarrollados y publicados en 1954 [18]. Los estudios tratan sobre diversos aspectos de las sobretensiones provocadas por descargas atmosféricas en líneas aéreas, la determinación de la frecuencia de ocurrencia de descargas directas e indirectas y el cálculo de la tasa de faltas totales.

La corriente de la primera descarga de retorno se define por su forma y parámetros característicos. El valor de la amplitud de la corriente sigue una ley de probabilidad dada por la probabilidad acumulativa de la corriente, como se muestra en (2). Según [2], [19], la probabilidad acumulada de la corriente puede ser calculada aproximadamente por:

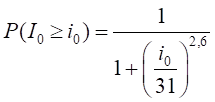
(1)

Donde:

i₀ es la corriente de la primera descarga de retorno (kA);

I₀ también llamada de I_50% es el promedio de los valores de pico das corrientes de descarga atmosférica cuja probabilidad es de 50% (31kA según Anderson-Eriksson) [19];

P(I₀≥i₀) es la probabilidad de la corriente promedio de pico de la primera descarga de retorno I₀ sea mayor o igual que i₀.

A. Tasa de fallas por descargas directas

Para estimar del número de descargas de contorno sobre los extremos del aislador debido a la incidencia directa de rayos sobre una red aérea ubicada en campo abierto, en este trabajo es utilizada la ecuación (2). La cual fue obtenida en función de las distancias de atracción y probabilidad de ocurrencia de las amplitudes de las corrientes de descarga según el modelo electro-geométrico [2], [20]. La exposición de la línea de distribución frente a las descargas atmosféricas depende de la cantidad de estructuras adyacentes que sobresalen por encima del terreno circundante. Los árboles y los edificios también pueden tener un papel importante en el rendimiento de las líneas de distribución, ya que pueden interceptar muchas descargas atmosféricas que de otro modo podrían alcanzar la línea.

Para el cálculo del número de fallas por descargas directas en redes eléctricas ubicadas en regiones urbanas o arborizadas debe tenerse en cuenta el factor de blindaje Sf, [2] de acuerdo con la siguiente ecuación:

(2)

Donde:

N_dir es el número de fallas por descargas directas sobre 100km de línea por año (fallas/100km/año);

N_g es la densidad de descargas a tierra (rayos/km²/año);

b es el ancho de la estructura o distancia máxima entre conductores de fase (m);

h_eficaz es la altura eficaz o altura máxima de la estructura (m);

P(I₀ ≥ i₀) es la probabilidad de la corriente de la primera descarga de retorno;

Sf_der y Sf_izq son los coeficientes de blindaje para los lados derecho e izquierdo de la línea.

B. Tasa de fallas por descargas indirectas

El número de fallas por descargas de contorno en aisladores por sobretensiones inducidas, provocadas por descargas indirectas, por 100km de línea por año (N_ind) puede ser estimado de acuerdo con:

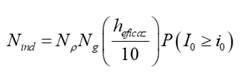
(3)

Donde:

N_ind es el número de descargas disruptivas por sobretensiones inducidas (fallas/100km/año);

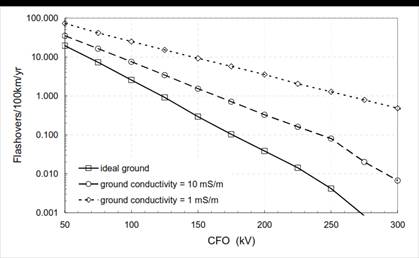
N_ρ es el número de descargas indirectas (fallas/100km/año) por la Fig. 1;

N_g es la densidad de descargas a tierra (descargas/100km²/año);

h_eficaz es la altura real de la estructura o altura eficaz (m);

P(I₀ ≥ i₀) es la probabilidad que la corriente de pico de la primera descarga de retorno I₀ sea mayor o igual que i₀.

Fig. 1. Fallas debido a tensiones inducidas Nρ vs nivel de aislamiento CFO de la línea de distribución [2].

C. Tasa de fallas totales

El número de descargas de contorno totales sobre una red aérea de distribución es la suma del número de fallas por descargas directas y por sobretensiones inducidas, según se muestra en (4). Todas las descargas de contorno (fallas por descargas directas e indirectas) son asumidas que causan faltas en el sistema [2]. La tasa de faltas por descargas atmosféricas en alimentadores de distribución es cuantificada por N_Total.

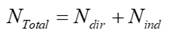
(4)

Donde:

N_Total es el número de descargas de contorno totales (fallas/100km/año);

N_ind es el número de descargas de contorno por tensiones inducidas (fallas/100km/año);

N_dir es el número de descargas de contorno debido a descargas directas (fallas/100km/año).

3. Metodología Utilizada

A. Sistemas de protección contra descargas atmosféricas

La evaluación del desempeño de los sistemas de distribución bajo condiciones de rayos requiere el modelado de los componentes del SDEE en el análisis de transitorios electromagnéticos. Varios estudios han sido publicados sobre modelado de sistemas de potencia en análisis transitorios [2], [21]. En este trabajo, los modelos y parámetros del sistema se utilizan de acuerdo con [11]-[15].

Un cable de guarda aterrado colocado como blindaje encima de los conductores de fase de alimentadores de distribución aéreos permite: i) la reducción del número de impactos directos en los conductores de fase; ii) la reducción de las sobretensiones inducidas a partir de campos electromagnéticos generados externamente por las descargas próximas a la línea; iii) la disminución de la impedancia característica del cable de guarda y su conexión a tierra; y iv) el aumento de la impedancia mutua del cable de guarda y su conexión a tierra con los conductores de fase protegidos [2]. De la misma forma, los captores Franklin conectados a los sistemas de puesta a tierra (PAT) proporcionan blindaje y protección para alimentadores de distribución aéreos frente a las descargas atmosféricas. 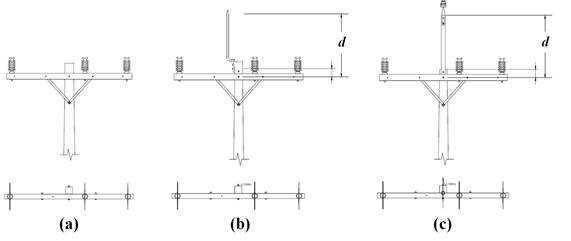Actualmente, las concesionarias de distribución utilizan varias configuraciones de estructuras. Fig. 2 ilustra los diferentes tipos de estructuras (postes y crucetas) consideradas en este trabajo: (a) sin blindaje, (b) con captor de Franklin y (c) con cable de guarda; donde la distancia d = 1m.

Fig. 2. Estructuras: (a) sin blindaje; (b) con captor Franklin y (c) con cable de guarda.

La Fig. 3 ilustra la configuración de la PAT considerada en este trabajo. El cálculo analítico de la resistencia de PAT para una malla es calculado de acuerdo a las ecuaciones presentadas en [22]. Se consideran conductores de cobre de 19 mm de diámetro y una longitud de 2,4m. Los conductores utilizados en la interconexión de las PAT y los cables de bajada de las estructuras son de cobre con diámetros que varían de 4 a 2 AWG. Las conexiones son hechas por conectores de tornillo, de tipo cuña o soldaduras exotérmicas.

Fig. 3. Puesta a tierra tipo malla utilizado en sistemas de distribución (adaptada de [22]).

Para simular las sobretensiones por descargas atmosféricas directas y/o sobretensiones inducidas producidas por descargas indirectas en la vecindad del alimentador de distribución se utiliza el software de transitorios electromagnéticos ATPDraw [23] y su herramienta TACS-MODELS [24]. Con el ATPDraw, se simularon diversos casos, donde se obtuvo la corriente crítica que produce la descarga disruptiva en los extremos del aislador para cada tipo de estructura (combinación de poste y PAT). Las líneas aéreas fueron modeladas con parámetros distribuidos dependientes de la frecuencia con modelo JMarti; las cargas a través de bloques ZIP; las PAT, conductores de interconexión y los postes fueron modelados con parámetros concentrados. Las condiciones de simulación fueron consideradas: la amplitud de la corriente de la descarga se varió entre 0,1kA - 20kA; la resistividad del suelo varía entre 100 y 2000; y el factor de blindaje se adoptó valores de blindaje nulos (Sf = 0) para regiones de campo abierto sin vegetación y en regiones con presencia de árboles o edificaciones en ciudades debido a la protección se adoptó valores de blindaje unitarios (Sf = 1), para todos las configuraciones de estructuras (combinaciones de postes y sistema de PAT).

B. Tasas de faltas permanentes y temporarias

La descarga de contorno puede llevar tanto a una falta momentánea o permanente. Con el fin de estudiar el impacto de las descargas atmosféricas sobre el rendimiento del sistema, es necesario identificar el número de falta momentánea λ y el número de falta permanente γ causada por una descarga atmosférica. En este trabajo la tasa de faltas permanentes Γ es asumida como siendo el 20% de las faltas totales. El número de faltas permanentes γ y el número de faltas momentáneas λ se calcula a partir de la relación o tasa de faltas permanentes Γ de acuerdo con las ecuaciones (5) y (6).

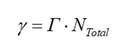
(5)

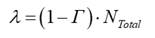
(6)

Donde: γ es el número de faltas permanentes (faltas/100km/año); Γ es la relación entre el número de faltas permanentes y el número total de faltas; λ es el número de faltas temporarias (faltas/100km/año).

C. Indicadores de confiabilidad

Los indicadores de confiabilidad comúnmente usados para medir la calidad de la energía eléctrica de los Servicios Públicos son el SAIFI y el MAIFI_E, son considerados por las Concesionarias de Servicios de Distribución y también fueron considerados en este trabajo [25]. La generalización de los indicadores de confiabilidad SAIFI_ij y MAIFI_Eij para una disposición arbitraria de la estructura-puesta a tierra j se obtiene en (7) y (8). La asignación de estructura-puesta a tierra j para cada sección de línea i del alimentador se puede escribir por la variable binaria x_ij definida en (9).

(7)

(8)

(9)

Donde:

i es la variable referente a la sección del alimentador (1 ≤ i ≤ ns);

j es la variable referente a la estructura-puesta a tierra (1 ≤ j ≤ ne);

ns es el número de secciones del alimentador;

ne es el número de estructuras-puestas a tierra;

x_ij es la variable binaria referente a la estructura-puesta a tierra j localizada en la sección de línea i;

SAIFI_ij es la contribución al indicador de confiabilidad SAIFI de la sección de línea i y secciones ubicadas aguas abajo, referente a la estructura-puesta a tierra j;

MAIFI_Eij es la contribución al indicador de confiabilidad MAIFI_E de la sección de línea i y secciones ubicadas aguas abajo, referente a la estructura-puesta a tierra j;

G es el conjunto de combinaciones de estructuras-puestas a tierra j posibles para todas las secciones de línea i del alimentador (ne x ns variables).

4. Optimización de los Indicadores de Confiabilidad del Sistema Utilizando PLIMM

El modelo PLIMM pretende alcanzar 3 objetivos simultáneamente: SAIFI, MAIFI_E y el costo de inversión. Este modelo es formulado como un problema de Programación Lineal Entera Mixta Multi-objetivos (PLIMM), visando el balance óptimo entre estos objetivos.

La programación por metas es una técnica de optimización multi-objetivo basada en el concepto de satisfacer una serie de objetivos, intentando alcanzar un conjunto de metas lo más cerca posible [26]. El método de programación por metas es utilizado en este trabajo, la idea básica es que se especifican niveles de aspiración para la función objetivo, siendo minimizada la suma ponderada de las desviaciones de estos niveles de aspiración. Esto se conoce como programación por metas ponderada. Una función objetivo (FO) en conjunto con restricciones con un nivel de aspiración de cada objetivo. Los niveles de aspiración se seleccionan de modo que no se puedan alcanzar simultáneamente. La formulación algebraica del modelo de programación por metas fue presentada por primera vez en [27].

Las metas se definen como:

- Meta 1 es dada por el indicador SAIFI;

- Meta 2 es dada por el indicador MAIFI_E;

- Meta 3 es dada por el costo de inversión de la concesionaria.

Las restricciones son distintas consideraciones técnico-económicas como así también la selección de un único conjunto de estructura-puesta a tierra para cada sección de línea del alimentador.

El modelo PLIMM propuesto tiene la formulación dada por (10).

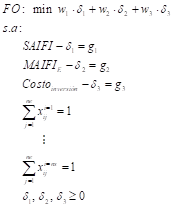
(10)

Donde:

Costo_inversión es el costo de inversión de la concesionaria (R$);

δ₁ es el desvío de SAIFI en relación a la meta g₁;

g₁ es la meta para el objetivo SAIFI;

δ₂ es el desvió de MAIFI_E en relación a la meta g₂;

g₂ es la meta para el objetivo MAIFI_E;

δ₃ es el desvío de Costo_inversión en relación a la meta g₃;

g₃ es la meta para el objetivo Costo_inversión;

w₁, w₂ e w₃ son los factores de normalización.

Los factores de normalización w₁, w₂ e w₃ son dados por (11), (12) e (13), respectivamente:

	(11)
	(12)
	(13)

Donde:

SAIFI^Máx y MAIFI_E^Máx son los máximos valores de SAIFI y MAIFI_E;

Costo_inversión^Máx es el máximo valor de inversión de la concesionaria (R$).

En la Fig. 4 se presenta el diagrama de flujo que muestra la metodología propuesta para optimizar la confiabilidad del SDEE formulada como un problema PLIMM y medida por los indicadores de confiabilidad SAIFI y MAIFI_E considerando los costos de las inversiones.

Fig. 4. Diagrama de Flujo del modelo PLIMM para optimización de los indicadores de confiabilidad y de inversión del sistema.

5. Estudio de Caso y Resultados

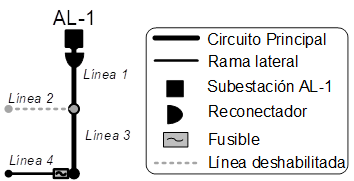
Para el estudio de caso se utiliza un sistema de prueba de 4 barras y 3 secciones de líneas correspondiente a la línea 1, línea 3 y línea 4 del alimentador de distribución descrito en la Fig. 5.

Fig. 5. Diagrama unifilar del sistema prueba de 4 barras.

La variable binaria, definida como x_ij, muestra la estructura-puesta a tierra ubicada en la sección de línea i. Los tipos de estructura-puesta a tierra j se describen a continuación:

1- SB (estructura sin blindaje);

2- CF_Malla (estructura con captor Franklin y puesta a tierra tipo malla);

3- CG_Malla (estructura con cable de guarda y puesta a tierra tipo malla).

En esta sección, se muestra la validación del modelo PLIMM para obtener simultáneamente los indicadores de confiabilidad (SAIFI y MAIFI_E) deseados y la inversión en el sistema (Costo_inversión). A continuación, se presentan las combinaciones posibles en la Tabla 1, la cual está ranqueada de acuerdo con valores crecientes de inversiones para que pueda ser hecha la comparación entre el valor de la restricción y el valor simulado por el algoritmo de optimización PLIMM.

Tabla 1. Combinaciones Posibles de Estructuras-PAT vs Indicadores de Confiabilidad e Inversión – En orden Creciente de Inversión.

Comb. n°	Línea 1	Línea 3	Línea 4	Inversión [R$]	*SAIFI* [int.perm/año]	*MAIFI_E* [int.mom./año]
1	SB	SB	SB	0	0,158227	0,825548
2	SB	SB	CF_Malla	2452	0,158044	0,723405
10	CF_Malla	SB	SB	2578	0,133269	0,739493
4	SB	CF_Malla	SB	3329	0,126000	0,714430
3	SB	SB	CG_Malla	3393	0,157973	0,683805
19	CG_Malla	SB	SB	3568	0,123593	0,706130
7	SB	CG_Malla	SB	4607	0,113506	0,671351
11	CF_Malla	SB	CF_Malla	5030	0,133086	0,637349
5	SB	CF_Malla	CF_Malla	5781	0,125817	0,612287
13	CF_Malla	CF_Malla	SB	5907	0,101042	0,628375
12	CF_Malla	SB	CG_Malla	5971	0,133015	0,597749
20	CG_Malla	SB	CF_Malla	6020	0,123410	0,603986
6	SB	CF_Malla	CG_Malla	6722	0,125746	0,572687
22	CG_Malla	CF_Malla	SB	6897	0,091366	0,595012
21	CG_Malla	SB	CG_Malla	6961	0,123339	0,564386
8	SB	CG_Malla	CF_Malla	7059	0,113323	0,569207
16	CF_Malla	CG_Malla	SB	7185	0,088548	0,585296
9	SB	CG_Malla	CG_Malla	8000	0,113252	0,529607
25	CG_Malla	CG_Malla	SB	8174	0,078872	0,551933
14	CF_Malla	CF_Malla	CF_Malla	8359	0,100859	0,526231
15	CF_Malla	CF_Malla	CG_Malla	9300	0,100788	0,486631
23	CG_Malla	CF_Malla	CF_Malla	9349	0,091183	0,492869
17	CF_Malla	CG_Malla	CF_Malla	9637	0,088365	0,483152
24	CG_Malla	CF_Malla	CG_Malla	10290	0,091112	0,453269
18	CF_Malla	CG_Malla	CG_Malla	10578	0,088294	0,443552
26	CG_Malla	CG_Malla	CF_Malla	10626	0,078689	0,449789
27	CG_Malla	CG_Malla	CG_Malla	11567	0,078618	0,410189

Para las estructuras existentes (sin blindaje), la inversión es nula, o sea, Costo_inversión^Min = R$0. En esta condición, los indicadores de confiabilidad son SAIFI^Máx = 0,158227 (int. perm./año) y MAIFI_E^Máx = 0,825548 (int. mom./año).

Por otro lado, cuando se asignan estructuras con cable de guarda y puesta a tierra tipo malla, los indicadores de confiabilidad son SAIFI^MIN = 0,078618 (int. perm./año) y MAIFIE^Min = 0,410189 (int. mom./año). En este caso, el valor de inversión es Costo_inversión^Máx = R$11.567,00.

De acuerdo con la ecuación (10), los valores máximos se utilizan para calcular los factores de normalización o pesos w₁, w₂ y w₃ de la función objetivo FO, y son dados por:

w₁ = 1 / (SAIFI^Máx) = 6,32 (int. perm./año)^-1;

w₂ = 1 / (MAIFIE^Máx) = 1,2113 (int. mom./año)^-1 y;

w₃ = 1 / (Costo_inversión^Máx) = 0,00008645 (R$)^-1.

Para definir los límites de las restricciones, se definen los niveles deseados o metas g₁, g₂ y g₃ referentes al SAIFI, MAIFI_E y Costo_inversión, respectivamente. Para el estudio de caso se comparan diversos escenarios para poder ver la potencialidad de la metodología PLIM, en cada escenario se seleccionan las metas g₁ y g₂ correspondientes a los indicadores de confiabilidad (SAIFI y MAIFI_E) los cuales están asociados a cada valor de inversión (Costo_inversión) definido como meta g₃.

Para el análisis del estudio de confiabilidad, es necesario considerar diversos casos de estudio, anteriormente llamados escenarios, donde se utilizan diferentes valores de las metas g₁, g₂ y g₃ según (10). A continuación, se describen los escenarios para validar el modelo de optimización simultánea de los indicadores de confiabilidad e inversión total formulados como un problema PLIMM. Para cada escenario, se cuantifican las metas g₁, g₂ y g₃ para los objetivos SAIFI, MAIFI_E y Costo_inversión, respectivamente.

Escenario 1:

g₁ = SAIFI = 0,13 (int. permanentes/año);

g₂ = MAIFI_E = 0,63 (int. momentáneas/año) y;

g₃ = Costo_inversión = R$5.000,00.

Escenario 2:

g₁ = SAIFI = 0,08 (int. permanentes/año);

g₂ = MAIFI_E = 0,55 (int. momentáneas/año) y;

g₃ = Costo_inversión = R$8.200,00.

Escenario 3:

g₁ = SAIFI = 0,078 (int. permanentes/año);

g₂ = MAIFI_E = 0,449 (int. momentáneas/año) y;

g₃ = Costo_inversión = R$10.700,00.

Los resultados obtenidos del modelo matemático de optimización utilizando PLIMM se presentan en la Tabla 2. Se puede observar que los resultados de las simulaciones están de acuerdo con los valores de las metas g₁, g₂ y g₃, correspondientes a los objetivos SAIFI, MAIFI_E y Costo_inversión, respectivamente, están marcadas en color azul, y los resultados de la simulación del solver GAMS en de color negro. Para cada escenario, la metodología de selección y asignación de estructura-puesta a tierra prioriza el menor valor posible de las desviaciones estándar δ₁, δ₂ y δ₃, de acuerdo con los pesos w₁, w₂ y w₃.

Tabla 2. Resultados de la Optimización de los Indicadores de Confiabilidad e Inversión vs Escenarios.

	Escenario 1	Escenario 2	Escenario 3
Combinación n°	11	25	26
g₁ [int./año]	0,13	0,078	0,078
δ₁ [int./año]	0,003	0,0009	6,89x10^-4
*SAIFI* [int./año]	0,133	0,0789	0,078689
g₂ [int./año]	0,63	0,55	0,449
δ₂ [int./año]	0,007	0,0019	7,9x10^-4
*MAIFI_E* [int./año]	0,637	0,5519	0,449789
g₃ [R$]	5.000,00	8.200,00	10.700,00
δ₃ [R$]	30,00	25,00	74,00
*Costo Inversión* [R$]	5.030,00	8.175,00	10.626,00
FO	0,031	0,058	0,001

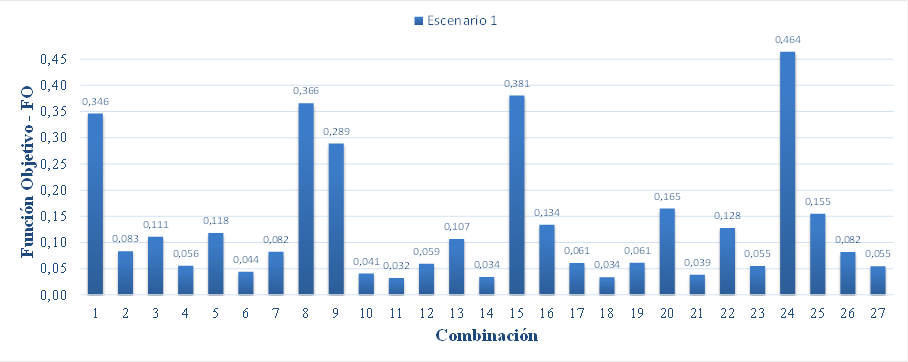
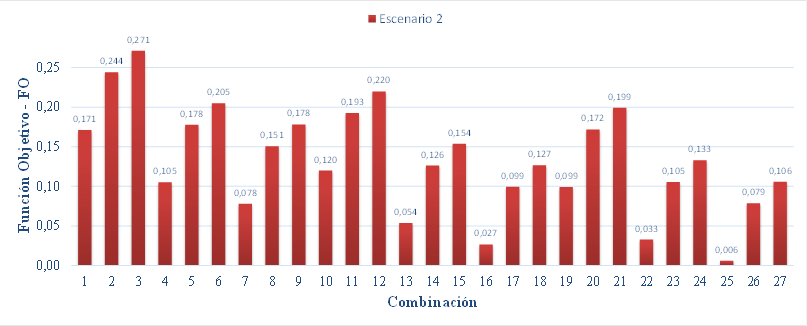
Los resultados de la FO calculada para los valores objetivos de los escenarios 1, 2 y 3 para cada combinación posible de estructuras-puesta a tierra, se presentan en la Fig. 6, Fig. 7 y Fig. 8.

Fig. 6. Función objetivo para cada combinación de estructura-puesta a tierra - Escenario 1.

Puede observarse en la Fig. 6 que la combinación 11 fue la que proporcionó la combinación de menor FO para el escenario 1. Este resultado coincide con el obtenido por el modelo PLIMM.

Fig. 7. Función objetivo para cada combinación de estructura-puesta a tierra - Escenario 2.

En la Fig. 7, se observa que la combinación 25 resultó en la menor FO para el escenario 2. Este resultado coincide con el obtenido por el modelo PLIMM.

Fig. 8. Función objetivo para cada combinación de estructura-puesta a tierra - Escenario 3.

Finalmente, la Fig. 8 muestra que la combinación 26 proporciona la menor FO para el escenario 3.

6. Conclusiones

Se presentó un nuevo modelo matemático utilizando PLIMM para la selección de SPDA en sistemas de distribución. La formulación propuesta se utiliza para seleccionar estructuras y puesta a tierra, a fin de alcanzar un balance óptimo entre las desviaciones de los indicadores de confiabilidad (SAIFI y MAIFI_E) y el costo de inversión del sistema (Costo_inversión). Tres tipos de topologías utilizadas como SPDA se probaron en cada sección del alimentador para obtener la solución óptima. Los resultados muestran que para el escenario 1 se eligió la combinación n° 11 que proporcionó el mayor valor de función objetivo igual a FO = 0,031 con indicadores de confiabilidad de SAIFI = 0,133 [int. perm./año], MAIFI_E = 0,637 [int. mom./año] y Costo_inversión = R$5.030. Por otro lado, en el escenario 3 se eligió la combinación n° 26 que proporcionó el menor valor de función objetivo FO = 0,001 con indicadores de confiabilidad de SAIFI = 0,078 [int. perm./año], MAIFI_E = 0,449 [int. mom./año] y Costo_inversión = R$10,626, en este caso la inversión disponible fue suficiente para instalar mejores SPDA en las secciones de línea.

La aplicación del modelo matemático de optimización utilizando PLIMM, permitió analizar la influencia de diversas estructuras-puestas a tierra como SPDA bajo la óptica sistémica. De acuerdo con los resultados de las pruebas presentadas, la aplicación del modelo matemático propuesto para optimizar la selección y asignación de la estructura-puesta a tierra como SPDA tiene potencial para mejorar la confiabilidad del sistema. El modelo matemático de optimización propuesto proporciona una ganancia significativa para las empresas distribuidoras de energía eléctrica. A través de la utilización de la metodología presentada las empresas de distribución de energía eléctrica pueden conocer para cada posible combinación los indicadores de confiabilidad SAIFI y MAIFI_E con la inversión y obtener mejoras significativas de sus redes de distribución. En este trabajo se utiliza un sistema reducido de 4 barras a modo de “validar y demostrar la eficacia del modelo PLIMM” mediante la verificación de la convergencia de resultados respecto de las metas y objetivos propuestos, siendo que en el trabajo [28] se analizó la sensibilidad del modelo PLIMM ante la variación de diversos parámetros.

Referencias

[1] IEEE Guide for Improving the Lightning Performance of Transmission Lines, IEEE Std.1243-1997, 1997.

[2] IEEE Guide for Improving the Lightning Performance of Electric Power Overhead Distribution Lines, IEEE Std.1410-2010, 2010.

[3] P. Chowdhuri, et al, “Parameters of Lightning Strokes: A review,” IEEE Trans. on Power Delivery, v.20, pp.346-358. Jan 2005.

[4] I. Uglesic, V. Milardic, B. Francg, et al. “Correlation between Lightning Impacts and Outages of Transmission Lines,” in 2012 CIGRE C4 Colloquium on Power Quality and Lightning, Sarajevo, Bosnia and Herzegovina, 13 – 16 May, 2012.

[5] A. P. Paes Dos Santos, J. R. Santos De Souza, A. Uglesic, V. Milardic, B. Francg, et al. “Electric Systems Failures Produced by CG Lightning in Eastern Amazonia,” Revista Brasileira de Meteorologia, v. 29, n. esp, 31 - 40, São Paulo Dec. 2014.

[6] A. C. Alameida, B. P. Rocha, J. R. S. Souza, J. A. S. Sá, J. A. Pissolato Filho, “Cloud-to-Ground Lightning Observations over the Eastern Amazon Region,” Atmospheric Research ELSEVIER, v.117, 1, p. 86–90. 2012.

[7] B. R. P. Rocha, et al, “Lightning Characteristics Time Distribution over Four Locations in Eastern Amazonia,” in: IX International Symposium on Lightning Protection, 2007. Anais... Foz do Iguaçú, 26 a 29 de November, 2007.

[8] Bollen, M. H. J. Understanding Power Quality Problems: Voltage Sags and Interruptions. 1.ed. New York: IEEE Press Series on Power Engineering – Edition John Wiley & Sons, Inc., 2000.

[9] AGÊNCIA NACIONAL DE ENERGIA ELÉTRICA. ANEEL, PRODIST - Procedimentos de Distribuição de Energia Elétrica no Sistema Elétrico Nacional. Módulo 8: Qualidade da Energia Elétrica. Brasília, DF, 2012. [Online]. Available: <http://www.aneel.gov.br/arquivos/PDF/Módulo8_Revisão_4.pdf>.

[10] S. P. Silva, A. Piantini, J. L. Franco; J. Gonçalves. Lightning Performance Studies for a 13.8 kV Distribution Network, In: SIPDA 2003- International Symposium on Lightning Protection, 7, 2003, Curitiba, 2003b, p. 137-143

[11] R. J. Cabral, D. S. Gazzana, R. C. Leborgne, A. S. Bretas, G. A. D. Dias, M. Telló, “Analysis of Distribution Lines Performance Against Lightning Using ATP-EMTP,” in EMC 2012 - IEEE International Symposium on Electro-Magnetic Compatibility Europe, Rome, Sept. 2012.

[12] R. J. Cabral, D. S. Gazzana, R. C. Leborgne, A. S. Bretas, G. A. D. Dias, M. Telló, “Improvement of an Overhead Distribution Feeder Performance Against Lightning Considering the Wire-Guard Protection,” in ICLP 2012 – IEEE International Conference on Lightning Protection, 31, Vienna, Sept. 2012.

[13] R. J. Cabral, D. S. Gazzana, R. C. Leborgne, A. S. Bretas, G. A. D. Dias, D Schwanz, M. Telló, “Effect of Shielding and Grounding on Lightning Performance of 23kV Distribution Feeders,” in NAPS 2013 - IEEE 45th North American Power Symposium, Manhattan, Sept. 2013.

[14] R. J. Cabral, D. S. Gazzana, R. C. Leborgne, A. S. Bretas, G. A. D. Dias, M. Telló, J. Morales, E. A. Orduña, “Improved Distribution Feeder Topology Against Lightning,” in SIPDA 2013 – IEEE XII International Symposium on Lightning Protection, Belo Horizonte, Oct. 2013.

[15] R. J. Cabral, A. S. Bretas, R. C. Leborgne, Morales, E. A. Orduña, “Sensitivity Assessment of Lightning-Induced Surges in Distribution Feeders Using ATP,” in DPSP 2014 - IET XII International Conference on Developments in Power System Protection, Copenhagen, Apr. 2014.

[16] J. Morales, E. A. Orduña, R. J. Cabral, A. S. Bretas, C. Rehtanz, “Novel Methodology for Analysis and Study of Distribution Feeder Performance Against Lightning Disturbances,” in DPSP 2014 - IET XII International Conference on Developments in Power System Protection, Copenhagen, Apr. 2014.

[17] “GAMS - General Algebraic Modeling System”. [Online]. Available: <http://www.gams.com>.

[18] Golde, R. H. “Lightning Surges on Overhead Distribution Lines Caused by Indirect and Direct Lightning Strokes,” Trans. of American Inst. of Electrical Engineers, v.73, n.1, p.437-447, Jan. 1954.

[19] Anderson, R. B., Eriksson, A. J. “Lightning Parameters for Engineering Application,” ELECTRA CIGRÉ, n. 69, p. 65-101, March 1980.

[20] Eriksson, A. J. “The Incidence of Lightning Strikes to Power Lines,” IEEE Transactions on Power Delivery, v. PWRD-2, n.2, p. 859-870, Jul. 1987.

[21] J. A. Martinez, F. A. Castro-Aranda, “Lightning Performance Analysis of Overhead Transmission Lines Using the EMTP,” IEEE Trans. on Power Del., vol. 20, no. 3, p. 2200-2210, Jul, 2005.

[22] IEEE Guide for Safety in AC Substation Grounding, ANSI/IEEE Std.80-2000, New York, 2000.

[23] H. W. DOMMEL, ElectroMagnetic Transients Program. Reference Manual (EMTP Theory Book), Bonneville Power Administration, Portland, 1986.

[24] L. Dube, Users Guide to MODELS in ATP, April 1996. 150p.

[25] IEEE Guide for Electric Power Distribution Reliability Indices, IEEE Std. 1366, 2003.

[26] Tamiz, M.; Jones, D.; Romero, C. Goal Programming for Decision Making: An Overview of the Current State-of-the-art, Transactions on European Journal of Operational Research, p. 569-581, n. 111, 1998.

[27] Miettinen, K. M. Nonlinear Multiobjective Optimization, Norwell, Kluwer Academic Publishers, 1999, p. 121-122.

[28] Bretas, A. S.; Cabral, R. J.; Leborgne, R. C.; Ferreira G. D.; Morales J. A. Multi-Objective MILP Model for Distribution Systems Reliability Optimization: a Lightning Protection System Design Approach. IJEPES Elsevier, v. 98, p. 256-268, June 2018.