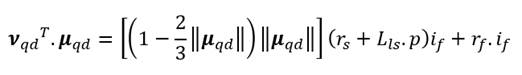SÍMBOLOS
p Potencia activa instantánea
q Potencia reactiva instantánea
α-β Componente en
marco de referencia estacionario
abc Componentes
del marco de referencia de la máquina
qd Componentes
en marco de referencia arbitrario
v Compontes de tensión
i Componentes de corriente
λ Componentes del flujo magnético
μ Factor de severidad de falla
Ns Total de espiras del bobinado de una fase
rs Resistencia de estátor
rr Resistencia de rotor
Lls Inductancia de dispersión
Lm Inductancia de dispersión
rf Resistencia
de falla
if Corriente de falla.
R Matriz de transformación
k Componente de frecuencia.
f Frecuencia de la red.
t tiempo.
LPF Filtro
pasabajos
VUF Factor
de desbalance de tensión
THDv Factor de distorsión de tensión
1.
Introducción
Las máquinas de inducción
(MI) trifásicas son utilizadas en la mayoría de los procesos de productivos en
las industrias. Los diferentes esfuerzos eléctricos y mecánicos a los que se
encuentran sometidas pueden ocasionar fallas en sus partes constitutivas
provocando paradas imprevistas del proceso e, inevitablemente, pérdidas
económicas. Los cortocircuitos entre espiras del bobinado son las averías de
mayor relevancia que ocurren en el estátor de las MIs. Este tipo de avería se
produce debido a la degradación progresiva del aislamiento entre los
conductores que conforman las espiras del bobinado. Un bobinado dañado ocasiona
una corriente de falla cuya magnitud puede superar varias veces la corriente
nominal de operación [1][2] lo cual puede ocasionar cortocircuitos entre fases
o entre fase y tierra. Por esto, es importante detectar este tipo de fallas en
su estado incipiente con el fin de ejecutar medidas preventivas y así evitar la
destrucción total de la máquina.
Para la detección de
averías existen varios métodos, algunos de ellos basados en la medición de la
tensión y corriente de fase. Estos analizan el comportamiento dinámico de las
corrientes en componentes de secuencia con el objeto de detectar asimetrías tanto
en el estátor como el rotor [3-5]. En trabajos recientes, la avería se estudia
mediante un modelo con falla en los bobinados de estátor considerando los
armónicos en la tensión de alimentación [6]. El modelo está desarrollado en
componentes de secuencias para el estado estacionario derivado del modelo
dinámico con falla en un marco de referencia qd. Una característica
interesante del trabajo propuesto es la posibilidad de detectar un
cortocircuito entre espiras del bobinado a partir del seguimiento de los
armónicos de la red, particularmente el 5to armónico. Entre otras estrategias
usadas para la detección y el diagnostico de fallas en las MI se encuentra el
uso de la teoría de la potencia instantánea (TPI) [7]. Esta teoría permite
separar las corrientes de estátor en componentes que depende de la potencia
activa y reactiva instantánea. La teoría es aplicada principalmente para
resolver problemas en la calidad de la energía y en desarrollos de filtros
activos. Sin embargo, en [8] y [9] se propone una técnica para el diagnóstico
de barras rotas en el rotor y las oscilaciones de carga en MI empleando las
componentes de corrientes activa y reactiva en marco de referencia α-β.
Los resultados presentados demostraron que es posible diagnosticar una falla en
el rotor dado que las firmas de las componentes de corrientes presentan efectos
bien diferenciados entre la falla y las oscilaciones de carga en el eje.
Con el objetivo de
desarrollar nuevos métodos de diagnóstico de averías en el estátor del MI, en
este trabajo se propone una metodología para detectar cortocircuito entre
espiras en los bobinados de estátor una MI utilizando la TPI [7]. Para este
propósito, se utiliza el modelo dinámico de la MI con falla propuesto en [6]
mediante el cual se calculan las corrientes y las tensiones incluyendo los
efectos de la avería en los bobinados del estátor.
A partir de las señales eléctricas,
se obtienen dos componentes de corriente en α-β a través de la
transformada de Clarke, una de ellas que depende de la potencia activa y la
otra de la potencia reactiva. Con las componentes de corriente, se analiza la
traza en el plano α-β para evaluar los efectos de la avería
considerando el 5to armónico en la tensión de alimentación. Se presentan
resultados para la máquina en condiciones normales de funcionamiento (sin
averías) y para distintas severidades de falla con tensiones de alimentación desequilibradas
y distorsionadas que incluyen el 5to armónico.
2.
Modelo del Motor a Inducción
con Avería
Para analizar
los efectos de la falla en el estátor se utiliza un modelo dinámico de la MI
con falla propuesto en [6]. Este modelo permite incluir un cortocircuito entre
espiras en bobinados de la MI incluyendo componentes armónicos en las tensiones
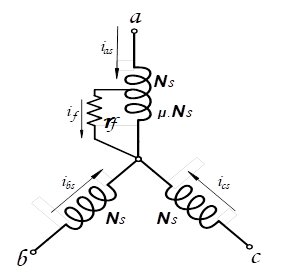
de alimentación. En la Fig. 1 se presenta un esquema del bobinado con falla en
la fase a.
Fig. 1 - Modelo de la MI con avería en bobinados.
El modelo
de la MI con falla en marco de referencia qd se presenta a continuación:
Y los flujos de estátor y rotor vienen
dados por:
|
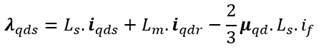
|
(4)
|
|
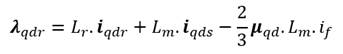
|
(5)
|
donde los subíndices s y r, indican las magnitudes
referidas al estátor y rotor respectivamente. V, i y λ
son vectores de tensión, corriente y flujo, respectivamente. En la Fig. 1 se representa gráficamente el modelo
de la máquina descripta en las ecuaciones (1) y (5) donde μ
representa el porcentaje de espiras afectadas en el cortocircuito respecto del
total de espiras del bobinado Ns, rf y if
es la resistencia y la corriente de falla respectivamente.
3.
Método de Detección de
Avería Propuesto
El método de
detección propuesto se basa en el procesamiento de señales eléctricas medidas
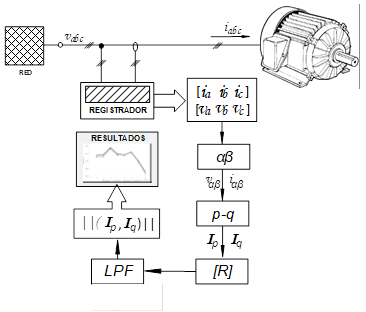
sobre bornes del estátor de la máquina. La metodología propuesta se muestra en
un esquemático detallado en Fig. 2. Las tensiones de alimentación aplicadas
desde la RED fueron distorsionadas incluyendo el 5to armónico con el fin de analizar
los efectos de la avería en dicha frecuencia.
Fig. 2 - Diagrama secuencial de la metodología
aplicada.
Las
corrientes y tensiones en marco de referencia abc se registran para su
posterior procesamiento. Luego, a través de la trasformada de Clarke se
obtienen las corrientes iαβ en el marco de
referencia estacionario α-β. En este referencial se obtiene
las componentes de corrientes utilizando la teoría de potencia instantánea [7].
Con el fin de separar las componentes armónicas para su posterior análisis se
procede a descomponer las corrientes en un marco referencial arbitrario y
rotatorio a la frecuencia que se desea separar de la señal completa, esta
transformación se realiza utilizando una matriz de transformación R.
Los ejes del marco de referencia arbitrario se definen como directo (d) y de
cuadratura (q). Las corrientes oscilatorias de frecuencia igual a la del marco
de referencia rotatorio se refleja sobre dicho marco como una señal de
continua. Una componente de señal con diferente velocidad angular a la del
marco se verá reflejada sobre este como una señal oscilante montada sobre la
componente de continua. Debido a la presencia frecuencias diferentes sobre las
componentes de continua, un filtro pasabajos (LPF) se implementó para
separar la componente fundamental. Este filtrado se implementó con un tipo Butterworth
de primer orden con frecuencia de corte en 60Hz.
3.1.
Componentes de Corrientes Activas y Reactivas
La teoría p-q
se basa en un conjunto de potencias instantáneas definidas en el dominio del
tiempo; por lo que es válida tanto en estados estacionario como para
transitorios. Esta teoría considera al sistema trifásico como una unidad,
transformando las tensiones y corrientes en marco de referencia abc a un
marco de referencia estacionario en variables α-β utilizando
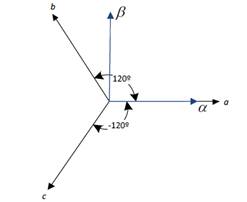
la transformación de Clarke [2]. En la Fig. 3 se muestra una representación gráfica
de esta transformación que permite interpretar el cambio de coordenadas que se
realizará con las señales eléctricas.
Fig. 3 - Representación gráfica de la transformada
de Clarke [2].
Para obtener
las potencias activa p y reactiva q se utilizan las tensiones y
corrientes instantáneas en marco de referencia α-β por medio
de la siguiente expresión:
|
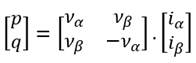
|
(6)
|
Las
corrientes activas y reactivas se obtienen aplicando las ecuaciones (7) a (10)
[7].
Corriente activa instantánea α:
|
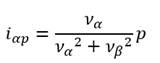
|
(7)
|
Corriente activa instantánea β:
|
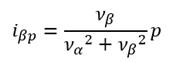
|
(8)
|
Corriente reactiva instantánea α:
|

|
(9)
|
Corriente reactiva instantánea β:
|
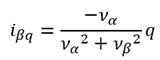
|
(10)
|
Las corrientes
obtenidas en (7)-(10) serán utilizadas para analizar los efectos de la avería
en el estátor.
3.2.
Traza de las componentes de corriente
A partir de las
corrientes activas y reactivas presentadas en las ecuaciones (7) a (10), es
posible generar dos vectores corrientes. Uno constituido por la parte activa de
la corriente de ambos ejes y otro con la parte reactiva. Analíticamente este
concepto se puede expresar como se muestra en las ecuaciones (11) y (12),
conocido como el vector de Park.
|
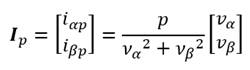
|
(11)
|
|

|
(12)
|
Para una MI balanceada y alimentada con
tensiones sinusoidales equilibradas, la traza del vector Park representada en
el plano α-β será una circunferencia ideal [10][11]. Haciendo esta analogía bajo las mismas
condiciones de operación, la traza de los vectores de corrientes de (11) y (12)
describirán una curva circular en el plano α-β. Por el contrario, bajo condiciones de
funcionamiento anormales esta traza se verá alterada según la perturbación que
produce el estado. El análisis de la traza de estos vectores corriente permitirá
visualizar la presencia o no de estados anormales de funcionamiento.
Las componentes de corrientes (11) y (12) se descomponen sobre un marco
referencial arbitrario y rotatorio a la frecuencia que se desea analizar, esta
transformación se realiza utilizando la siguiente matriz R,
definida como:
|
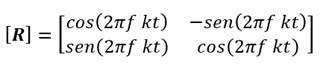
|
(13)
|
La señal oscilatoria de frecuencia
igual a la del marco de referencia R se refleja sobre dicho marco
como una señal de componente continua. Sin embargo, las componentes con
diferente velocidad angular se reflejan como señales oscilantes montadas sobre
la componente de continua. Luego se utiliza un filtro pasabajos (LPF) para
separar la magnitud de la componente armónica bajo análisis.
4.
Resultados de Simulación
El comportamiento de la MI con un
cortocircuito entre espiras en bobinados se evaluó mediante resultados de
simulación empleando el modelo dinámico de la MI presentado en la Sección 2.
Las simulaciones fueron realizadas para diferentes estados de operación y para distintas
severidades de averías con tensiones de alimentación desequilibradas y distorsionadas.
Los datos requeridos para la
implementación digital del modelo analítico tales como los parámetros
característicos, la velocidad y torque nominal, la cantidad total del número de
espiras que conforman el bobinado, se muestran en la Tabla 1.
Tabla 1 -
Características de la MI utilizada en las simulaciones
|
11,8 A
|
380 V
|
1450 rpm
|
50 Hz
|
|
rs
|
0,9 Ω
|
rr
|
0,4 Ω
|
|
Lls
|
4 mH
|
Lm
|
125 mH
|
|
Conexión
Bobinas
|
Serie
|
Bobinas/Fase
|
8
|
|
Espiras/Bobina
|
18
|
Espiras/Fase
|
144
|
Cabe mencionar que las características de
la MI simulada corresponden a un prototipo de MI que será utilizado para la validación
experimental del método de detección propuesto en este trabajo.
A
continuación, se mencionan las diferentes condiciones
de funcionamiento que fueron analizados en la MI cuando
se produce un cortocircuito entre espiras en los bobinados de una fase mediante
la evaluación de las componentes de corrientes activa y reactivas instantáneas,:
1)
Estado sin averías (Normal) y con desequilibrio de las tensiones de
alimentación;
2) Estado
sin averías (Normal) con distorsión y desequilibrio de las tensiones de
alimentación;
3)
Estado con avería (Falla) y con desequilibrio de las tensiones de alimentación
y;
4) Estado
con avería (Falla) con distorsión y desequilibrio de las tensiones de
alimentación.
Los ensayos se realizaron considerando una
distorsión de tensión máxima de THDv = 15% y diferentes VUF
(Factor de desbalance de tensión). Para los estados con avería se consideraron
severidades del 3,5% y 14% que corresponden a cortocircuitar 5 y 20 espiras del
bobinado, respecto del total que conforma una fase.
4.1.
Estado sin avería con tensiones de alimentación
desequilibradas
En este apartado se estudian los efetos del desequilibrio de tensión
sobre la MI en condiciones normales de operación. Los resultados obtenidos de
este caso de análisis son fundamentales dado que indican el comportamiento de
la máquina en condiciones de funcionamiento ideales para su posterior
comparación con estados de averías. En las Fig. 4 y Fig. 5 se observa la traza en plano α-β
de las componentes de corrientes para diferentes condiciones de operación. Para
el caso de la MI sin averías alimentada por un sistema polifásico perfectamente
balanceado, la traza en el plano describe una circunferencia ideal (traza de
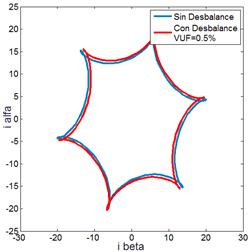
color azul). La Fig. 4 superpone
el caso para la MI sin averías y cuando existe un desequilibrio en las
tensiones de alimentación dado por el indicador VUF = 0,5 %; un valor
típico de desequilibrio que podemos encontrar en una red de alimentación
convencional (traza de color rojo). Con el fin de contrastar el efecto del
desequilibrio de tensiones de alimentación con los efectos de una avería de baja
severidad (pocas espiras dañadas en el bobinado, 3,5%), en la Fig. 5 se muestran las trazas obtenidas para
la MI sin averías y cuando se presenta un cortocircuito entre espiras.
Comparando ambas figuras puede observarse que los desequilibrios de la tensión de
alimentación producen efectos similares sobre la traza de corrientes, dificultando
la tarea de distinguir de manera precisa los efectos de una avería con tan sólo
visualizar la traza en el plano α y β.
|
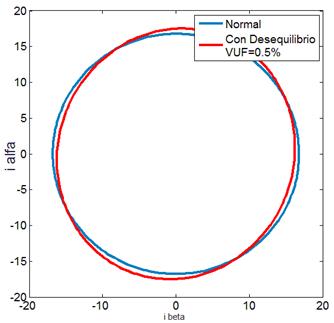
Fig. 4 - MI en estado de operación sin avería y
con desequilibrio de tensiones de alimentación.
|
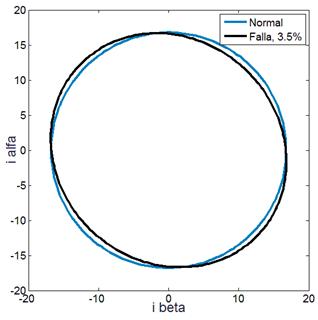
Fig. 5 – MI en
estado de operación sin avería y con una avería en los bobinado de la fase a.
|
4.2.
Estado normal con tensiones de alimentación
distorsionadas y desequilibradas
En este caso analizado
la MI opera bajo condiciones de funcionamiento normales alimentada mediante un
sistema polifásico, pero con THDv = 15% debido a la inclusión
del 5to armónico. En la Fig. 6
se muestra los resultados de simulación cuando se introduce un 5to armónico a
una red de alimentación sin desbalance de tensiones y con un desbalance de VUF
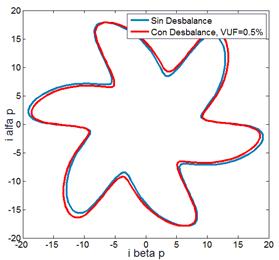
= 0,5 %. En la Fig. 6(a) se
muestra la traza del vector de Park, en la Fig. 6(b) la traza del vector de corriente
activo y en la Fig. 6(c) la
traza del vector de corriente reactivo. Comparando la Fig. 4 con la Fig. 6 (a), se observa una deformación de la
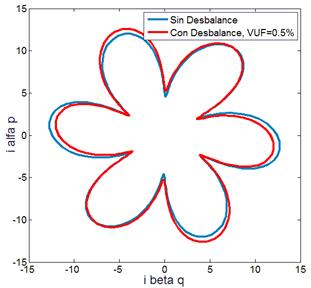
traza por la distorsión de tensión introducida. En la Fig. 6, las trazas que dependen de las
componentes de corrientes activas Fig. 6(b) y reactivas Fig. 6(c) se
diferencian entre sí, sin presentar una significativa alteración de patrones al
introducir un desequilibrio en la tensión aplicada.
Fig. 6 – MI sin
avería con desequilibrio y distorsión de tensión. (a) Vector de Park.
(b) Vector de
corriente activo. (c) Vector de corriente reactivo.
4.3.
Estado con avería con tensiones de alimentación
desequilibradas
En este apartado se estudia los efectos
de un cortocircuito entre espiras en bobinados de la MI cuando es alimentada
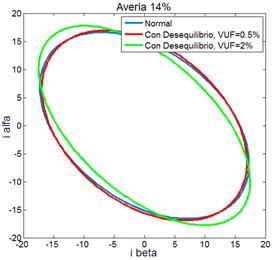
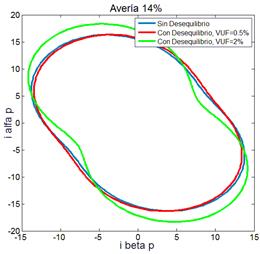
mediante un sistema de tensión polifásico. En la Fig. 7 se muestra los resultados de
simulación correspondiente al caso en que se produce un cortocircuito de
severidad 14% en bobinados de la fase a (20 espiras en cortocircuito) y
con tensiones de alimentación desequilibrada con VUF = 0,5 % y VUF
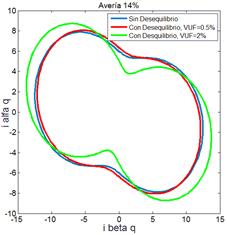
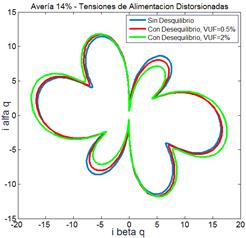
= 2%. En la Fig. 7 (a) se muestra la traza del vector de Park, en la parte Fig. 7 (b) y (c) la traza del vector de
corriente activo y reactivo, respectivamente, Comparando las Fig. 5 con la Fig. 7(a), se observa que a medida que se
incrementa la cantidad de espiras en cortocircuito, la traza del vector de Park
tiende a ser más elíptica y experimenta una rotación en el plano. Cada vector
de la Fig. 7 produce una traza
característica y diferente del resto. La traza de un mismo vector presenta
alteraciones perceptibles al introducir desbalances de la red mayores a VUF
= 2%.
Fig. 7 – MI con avería en bobinados (14%) y con
desequilibrio de tensión (a) Vector de Park. (b) Vector de corriente activo (c)
Vector de corriente reactivo.
4.4.
Estado con avería con tensiones de alimentación
desequilibradas y distorsionadas
En este caso la MI presenta un
cortocircuito entre espiras del bobinado y es alimentada mediante un sistema de
tensión polifásico con distorsión dada por THDv = 15% debido
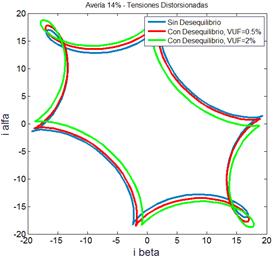
a la inclusión del 5to armónico. La Fig. 8 muestra los resultados de simulación
que resume una combinación de los efectos mostrados en las secciones
anteriores, es decir, considerando el 5to armónico en la tensión de
alimentación sin desequilibrio y con desequilibrio dado por VUF = 0,5 %
y VUF = 2%. La severidad de la avería se mantiene igual al 14% en el
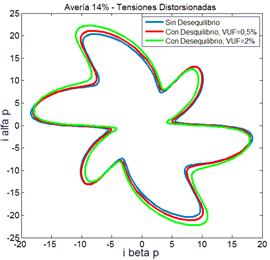
bobinado de la fase a de la MI. En la Fig. 8(a) se presentan la traza del vector
de Park, en la Fig. 8(b) y (c)
la traza del vector corriente activo y reactivo instantáneas, respectivamente.
Comparando la Fig. 8(a) con la Fig. 6(a), se observan trazas de similares características,
pero rotadas en el plano. Esto se debe a los efectos de un cortocircuito entre
espiras originado en bobinados de la fase a de la MI, produciendo
efectos similares al presentado en la sección anterior. Se observa además que
las señales mostradas en la Fig. 8 reproducen trazas bien diferente entre cada una de ellas en el
plano α-β. También es importante mencionar que al introducir
diferentes grados de desequilibrio de la tensión de alimentación no se producen
cambios significativos en las trazas de un mismo vector, manteniendo el mismo patrón
en el plano. Sin embargo, a medida que la severidad de la avería en bobinados
se incrementa puede observarse una rotación sobre el plano α-β
y, al mismo tiempo, tienden a deformarse comparando con el estado de la MI sin
avería.
Fig. 8 - MI con
avería en bobinados (14%) y con desequilibrio y distorsión de tensión (a)
Vector de Park.
(b) Vector de
corriente activo (c) Vector de corriente reactivo.
Por último, en la Fig. 9 y la Fig. 10 se muestran
las trazas de las corrientes activa y reactiva instantánea separados para la componente
de frecuencia fundamental y el 5to armónico contenida en la señal corriente.
Esta descomposición se realiza utilizando la matriz transformación R de la ecuación (13). Comparando la
Fig. 9 con la Fig. 7(a) presentan iguales características
ante los efectos de una avería y los desequilibrios de tensión. Sin embrago, analizando
la traza mostradas en la Fig. 10, originadas únicamente por las componentes
del 5to armónico de corrientes, puede visualizarse que los desequilibrios de la
tensión producen alteraciones menos significativas sobre la traza del vector de
Park. Esto último indica que los desequilibrios de tensión producen menos
efectos sobre la componente del 5to armónico de corriente, evitando de esta manera posibles errores en la detección.
|
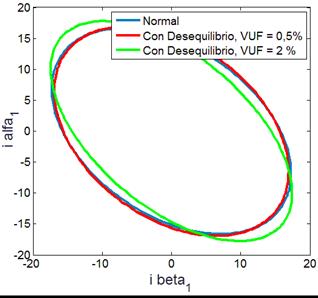
Fig. 9 – Traza del vector de Park de la componente
fundamental de corriente para la MI con avería (14%) con desequilibrio de
tensión.
|
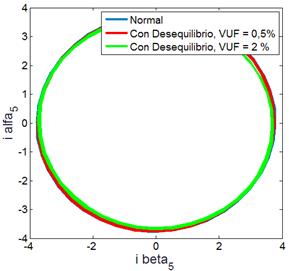
Fig. 10 – Traza del vector de Park de la quinta componente
armónica de corriente para la MI con avería (14%) con desequilibrio de
tensión.
|
5.
Conclusiones
En este trabajo se
presentó una metodología para detectar un cortocircuito entre espiras en
bobinados del estátor de las máquinas de inducción (MI) trifásica utilizando la
teoría de la potencia instantánea. La estrategia de
detección se basa en la medición de las tensiones y las corrientes de fase
sobre los bornes de la MI durante el normal funcionamiento. Para el análisis de
los efectos de un un cortocircuito entre espiras en los bobinados se utilizó un modelo dinámico que permitió
incluir averías de severidades diferente en cada una de las fases del estátor.
A
partir de las señales de corrientes y de tensión se utiliza la transformada de
Clarke para calcular dos componentes de corriente activa y reactiva instantánea
en marco de referencia α-β. En análisis de las trazas de las
componentes de corrientes en el plano α-β permitió evaluar los
efectos de una avería en bobinados considerando las tensiones de alimentación desequilibradas
y distorsionadas con la inclusión del 5to armónico en la tensión. Para
el caso de la MI sin averías con tensiones de alimentación equilibradas,
las trazas en el plano describen una circunferencia ideal. Sin embrago, ante una perturbación tales como el
desequilibrio de las tensiones o las averías, las trazas tienden a deformarse
con rotaciones en el plano α-β.
Se determinó que para bajas severidades de averías (5
espiras en cortocircuito) las trazas obtenidas presentan características similares
a las obtenidas a partir de los desequilibrios en la red de alimentación
típicos VUF = 5%, llegando a confundir los efectos de una avería de baja
severidad. Sin embrago, cuando la severidad de la avería se incrementa (20
espiras en cortocircuito) las trazas pueden ser diferenciadas de manera precisa,
incluso, para grados de desequilibrios de tensión significativos VUF = 2%.
Por
último, se determinó que los efectos de los desequilibrios de tensión sobre las
trazas del quinto armónico de corriente no modifican significativamente el
patrón descrito en el plano α-β. Por lo tanto, la traza del 5to
armónico puede ser de mucha utilidad para el desarrollo de estrategias de
diagnóstico capaces de aislar las averías de otras perturbaciones comunes en el
ámbito industrial como el desequilibrio o distorsión de las tensiones de
alimentación o los contactos de alta resistencia, entre otras. Como trabajo a
futuro se pretende analizar los efectos de otras perturbaciones y evaluar la
respuesta en frecuencia de las componentes de corrientes activa y reactiva
instantánea.
Agradecimientos
Este trabajo se llevó a cabo en el marco del Proyecto
de investigación denominado: “Diagnóstico de avería en los bobinados de
estátor de las máquinas eléctricas rotativas utilizando señales eléctricas”,
Cód. No 16/I162-PI. RES. C.S. No 082/16, gracias al financiamiento otorgado por
la Secretaria General de Ciencia y Tecnología de la Universidad Nacional de
Misiones (UNaM) y el Consejo Nacional de Investigaciones Científicas y Técnicas
(CONICET).
Referencias
[1]
Manuel. A. Mazzoletti,
G. R. Bossio, C. H. De Angelo, and D. R. Espinoza-Trejo, “Efectos del
cortocircuito entre espiras en maquinas síncronas de imanes permanentes”; en
2014 IEEE Biennial Congress of Argentina (ARGENCON), June 2014, pp.
531–536.
[2]
P. Krause, O.
Wasynczuk, s. Sudhoff, and S. Pekarek, Analysis of Electric Machinery and Drive
Systems, 3rd ed. New
Jersey, USA: IEEE Press, 2013.
[3]
F. Briz, M. W. Degner,
J. M. Guerrero, and P. Garcia, “Stator windings fault diagnostics of induction
machines operated from inverters and soft-starters using high-frequency
negative-sequence currents”; IEEE Transactions on Industry Applications,
vol. 45, no. 5, pp. 1637–1646, 2009.
[4]
J. Burriel-Valencia, R.
Puche-Panadero, M. Riera-Guasp, A. Sapena Bano, M. Pineda-Sanchez, and J.
Martinez-Roman, “Low computational cost algorithm for detecting rotor
asymmetries in im based on the negative sequence component of the startup
currents”; in 2017 IEEE 11th International Symposium on Diagnostics for
Electrical Machines, Power Electronics and Drives (SDEMPED), Aug 2017, pp.
628–634.
[5]
A. Berzoy, H. H.
Eldeeb, and O. A. Mohammed, “On-line detection of stator faults in DTC-driven
IM using SC impedance matrix off-diagonal term,” IEEE Transactions on
Industry Applications, vol. 55, no. 6, pp. 5906–5915, Nov 2019.
[6]
Manuel. A. Mazzoletti,
L. A. Barruffaldi, J. A. Potschka, M. O. Oliveira and G. R. Bossio,
"Steady-State Induction Machine Model with Turn Faults and Voltage
Harmonics," 2018 IEEE Biennial Congress of Argentina (ARGENCON),
San Miguel de Tucumán, Argentina, 2018, pp. 1-6.
[7]
H. Akagi, E. H.
Watanabe and M. Aredes, “Instantaneous Power Theory and Applications to Power
Conditioning”, Wiley-IEEE Press, 2007.
[8]
C. Pezzani, P. Donolo,
A. Castellino, G. Bossio and C. De Angelo, “Nuevo enfoque del vector corriente
para el diagnóstico de barras rotas y oscilaciones de carga en motores de
inducción”; XIII Reunión en Procesamiento de la Información y Control
(RPIC’09), 16 al 18 de Setiembre de 2009. Rosario, Argentina. ISBN:
950-665-340-2.
[9]
G. R. Bossio, C. H. De
Angelo, J. M. Bossio, C. M. Pezzani and G. O. Garcia, "Separating Broken
Rotor Bars and Load Oscillations on IM Fault Diagnosis Through the
Instantaneous Active and Reactive Currents," in IEEE Transactions on
Industrial Electronics, vol. 56, no. 11, pp. 4571-4580, Nov. 2009.]
[10]
A. J. Marques Cardoso,
S. M. A. Cruz, J. F. S. Carvalho, and E. S. Saraiva, "Rotor cage fault
diagnosis in three-phase induction motors, by Park's vector approach"; in
Industry Applications Conference, 1995. Thirtieth IAS Annual Meeting, IAS '95.,
Conference Record of the 1995 IEEE, 1995, pp. 642-646 vol.1.
[11]
N. Benouzza, A.
Benyettou, and A. Bendiabdellah, "An advanced Park's vectors approach for
rotor cage diagnosis"; First International Symposium on Control,
Communications and Signal Processing, pp. 461-464, 2004.