Elsevier instructions for the preparation of a 2-column-format camera ready paper

1. Introducción

Las Competencias Genéricas de Egreso del Ingeniero, propuestas por el Consejo Federal de Decanos de Ingeniería de Argentina (CONFEDI) y asumidas como propias por la Asociación Iberoamericana de Entidades de Enseñanza de la Ingeniería ASIBEI, contemplan cinco Competencias Tecnológicas y cinco Competencias Sociales, Políticas y Actitudinales. Entre las del segundo grupo, la primera que se encuentra es “desempeñarse de manera efectiva en equipos de trabajo” [1]. Se trata de una competencia cada vez más valorada en el ejercicio profesional y surgen nuevas demandas en las organizaciones modernas que hacen que el trabajo en equipo sea más vital y desafiante. Investigaciones recientes demuestran que esta competencia es crítica para el éxito en los trabajos del futuro [2].

En la Facultad de Ingeniería de la Universidad Nacional de Misiones (FIUNaM) un equipo docente llevó a cabo un proyecto de investigación entre 2011 y 2014, mediante el cual se formuló y aplicó un Modelo de Formación por Competencias (MFPC) en forma exitosa en la asignatura Investigación Operativa de la carrera de Ingeniería Industrial [3]. El MFPC se apoya sobre tres bases articuladas entre sí: la formulación de competencias, la mediación pedagógica y el sistema de evaluación de las competencias [4]. La Mediación Pedagógica, en términos simples, es el “cómo” del proceso de enseñanza y aprendizaje. Entre las modalidades de enseñanza-aprendizaje y los métodos didácticos, puede inferirse que el aprendizaje cooperativo en grupo puede ser el más apropiado para la formación para el trabajo en equipo, además de alcanzar otras competencias mediante esta estrategia.

No obstante, los grupos de trabajo deben estar adecuadamente diseñados, debiéndose establecer grupos de tamaños reducidos y preferentemente heterogéneos, porque el aprendizaje se alcanza mejor afrontando las diferencias, distintos puntos de vista e intereses [5]. Se presenta en este trabajo un procedimiento especialmente desarrollado para esta finalidad e implementado en una asignatura dentro del MFPC de la FIUNaM.

1.1. El trabajo en equipo y en grupo

La razón básica del trabajo en equipo es el mejor desempeño en una actividad, en comparación con el trabajo individual. Cuando las personas trabajan en cooperación pueden conseguir mucho más que trabajando en forma individual. Este es el principio de sinergia: la contribución del equipo es mayor que la suma de contribuciones de sus integrantes. En el ámbito educativo existen evidencias de que los estudiantes cuando trabajan en forma grupal y colaborativa logran aprendizajes difícilmente alcanzables en forma individual [6], [7].

En el funcionamiento de un equipo se observan dos dimensiones fundamentales: a) la tarea que debe realizarse y b) los factores sociales que influyen en el trabajo en conjunto. Este trabajo se enfoca en la segunda dimensión. Las personas tienen distintas características personales que influyen en el desempeño del equipo y necesidades que pueden satisfacerse o frustrarse trabajando de esta manera. Si se ignora cualquiera de estas dimensiones, difícilmente se alcance un desempeño eficiente [6]. Existen varias teorías que buscan explicar la relación entre los factores sociales y el desempeño de un equipo, una de ellas es la teoría composicional, centrada en los atributos personales de los individuos [8].

Una primera cuestión a definir es la diferencia entre un grupo y un equipo. Según West [6] un equipo se identifica por: 1) ser un grupo de personas relativamente pequeño que trabaja en una tarea bien definida y compleja; 2) poseen objetivos claros, desafiantes, compartidos, derivados directamente de la tarea que deben ejecutar; 3) debe haber conexión e interdependencia entre los miembros para alcanzar los objetivos; 4) deben desempeñar distintos roles dentro del equipo (aunque podrían duplicarse algunos roles) y 5) deben tener suficiente autonomía, autoridad y recursos para alcanzar los objetivos. Aldag y Kuzuhara [2] afirman que muchas veces el trabajo en grupo conduce a resultados aceptables, pero cuando la tarea es compleja el trabajo debe ser en equipo.

1.2. El aprendizaje cooperativo

En la literatura en algunos casos pueden encontrarse indistintamente los términos aprendizaje cooperativo y aprendizaje colaborativo, mientras que otros autores definen modalidades diferentes [9]. Johnson y Johnson [10] definen el aprendizaje cooperativo como el uso instruccional de pequeños grupos, para que los estudiantes trabajen juntos y se maximice el aprendizaje de cada uno de ellos. Los estudiantes discuten el material que deben aprender y se ayudan mutuamente en su comprensión [7]. Slavin [11] señala que los enfoques constructivistas utilizan ampliamente esta estrategia, sobre la teoría de que los estudiantes pueden descubrir y comprender más fácilmente si trabajan mutuamente. Johnson y Johnson [10] cuestionan que con frecuencia y por error, se pretenda que los estudiantes trabajen correctamente aplicando este método, sin que aún cuenten con las habilidades necesarias para hacerlo competentemente. Por ello, el aprendizaje cooperativo requiere una adecuada formación y maduración de cada grupo, para que finalmente alcancen a ser equipos.

1.3. Decisiones para armar grupos para el aprendizaje cooperativo

Johnson y Johnson [10] presentan una guía de decisiones previas a la aplicación del método, entre ellas decidir el tamaño de los grupos y asignar a los estudiantes a ellos. En cuanto al número de integrantes, no señalan un número ideal, pero sugieren utilizar grupos pequeños. Otros autores, como Slavin [11] y De Miguel Díaz [5] sugieren formar grupos con 4 a 6 estudiantes. Yeoh y Mohamad Nor [12] señalan que en un curso de ingeniería los mismos deben integrarse por 3 a 5 miembros.

En cuanto a la asignación, la mayoría de los autores de la bibliografía consultada concuerdan que deben conformarse grupos heterogéneos [5], [7], [10], [11], [13].

Por otra parte, debe prestarse atención a esta decisión, pues diferentes grupos de trabajo pueden producir distintos procesos de aprendizaje en los estudiantes [14]. En la literatura existen evidencias de relaciones entre las características de los grupos y el desempeño de sus integrantes. Sin embargo, el impacto de la diversidad en el rendimiento es un aspecto todavía poco estudiado [7].

Según Johnson y Johnson [10] la asignación puede ser aleatoria. Pero, de esta forma y aunque se realicen correcciones manuales, no siempre se pueden obtener grupos con las características deseadas y balanceados entre sí [12], [15]. Por otra parte, la experiencia demuestra que si se libera la conformación a los estudiantes, lo hacen por afinidades, por lo que tienden a formarse grupos homogéneos y no equivalentes entre sí [9]. Estos son motivos para utilizar otros métodos, algunos basados en modelos de programación matemática.

1.4. Modelización matemática para formar grupos heterogéneos

El modelo matemático general recibe el nombre de Problema de Agrupación de Máxima Diversidad (en inglés Maximally Diverse Grouping Problem - MDGP). Se busca con esta modelización particionar un conjunto de n- elementos en m-grupos disjuntos, de manera que se maximice la diversidad entre elementos de cada grupo. La diversidad entre elementos se calcula como la suma de valores de disimilitud d_ij entre cada par de elementos i y j. La formulación del MDGP corresponde a un problema de programación entera cuadrática. Su formulación es la siguiente [7], [16], [17], [18]:

Maximizar:

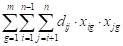
(1)

Sujeta a:

	(2)
	(3)
	(4)
	(5)

Donde x_ig es una variable binaria que toma valor 1 si el i-ésimo elemento forma parte del g-ésimo grupo y 0 en otro caso. La función objetivo (1) suma las distancias de todos los elementos que pertenecen a un mismo grupo. La restricción (2) asegura que cada elemento se asigne a un grupo. Las restricciones (3) y (4) establecen tamaños mínimo y máximo respectivamente para cada grupo. En ciertos casos puede asignarse el mismo número de elementos a cada grupo, de tal manera que 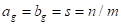, y (3) y (4) se sustituyen por una sola.

El modelo asume que cada elemento i se caracteriza por p_ik atributos, con i=1,…n y k= 1,…,t. La diversidad entre pares de elementos i y j debe darse por una función de distancia, que puede ser la distancia euclidiana [7], [16], [18]:

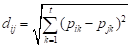
(6)

Para la resolución del MDGP, en la literatura se registran numerosos algoritmos exactos y heurísticos. Sin embargo, se trata de un problema combinatorio NP-completo, por lo que la práctica frecuente es aplicar algoritmos metaheurísticos. Entre los algoritmos se encuentran búsqueda tabú [16], búsqueda en vecindarios variables [18], algoritmos genéticos [14], colonias artificiales de abejas [17], entre otros métodos [7], [15].

En la literatura se observan críticas y modificaciones al modelo MDGP original. Baker y Powell [19] ofrecen una revisión de distintas funciones objetivo que pueden utilizarse para el mismo problema, que se diferencian principalmente por el criterio para medir la diversidad, tanto intra como inter-grupos. Sadeghi y Kardan [15] presentan una formulación alternativa, especialmente diseñada para el aprendizaje colaborativo. Se trata de un modelo de programación lineal entera-binaria, cuyo objetivo es la maximización de la compatibilidad de los individuos en los grupos.

En cuanto a los atributos para caracterizar a los estudiantes, en la literatura pueden hallarse distintos criterios. Pang et al. [7] consideran un conjunto de variables demográficas, académicas y de personalidad. En forma similar, Ounnas [9] presenta los atributos en tres categorías: académicos, personales y relacionales, y contextuales. Yeoh y Mohamad Nor [12] consideran la situación académica y variables demográficas. Sadeghi y Kardan [15], al igual que Pinninghoff et al. [14] emplean a atributos académicos y personales.

2. Metodología

Para el proyecto de investigación en curso se utiliza un enfoque mixto, combinando métodos cualitativos y cuantitativos, dentro del paradigma pragmático [20]. El diseño adoptado es de integración [21], recolectándose datos cuantitativos y cualitativos durante toda la investigación, los cuales pueden transformarse de un tipo a otro y combinarse entre sí. Este tipo de diseño es completamente iterativo y resulta apropiado al problema planteado, por su complejidad. Las técnicas e instrumentos utilizados son, entre otras, revisión documental y bibliográfica, técnicas de observación y encuestas semi-estructuradas, grupos de discusión y la triangulación.

La revisión bibliográfica incluyó material sobre trabajo y aprendizaje en grupos, y sobre Formación por Competencias. Luego se puso énfasis en los métodos para conformar grupos de trabajo, más precisamente modelos matemáticos y algoritmos de Investigación Operativa.

3. Resultados y Discusión

3.1. Método propuesto para formar grupos para el aprendizaje cooperativo

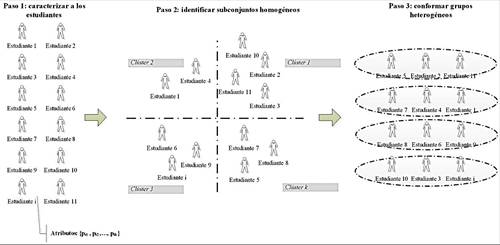
El procedimiento consiste en: 1) caracterizar a los estudiantes, utilizando múltiples atributos cuali y cuantitativos; 2) identificar subconjuntos homogéneos; 3) repartir a los estudiantes a los grupos que se desean conformar, partiendo de los subconjuntos obtenidos en el paso anterior. El procedimiento se esquematiza en la Fig. 1 y sus pasos se describen a continuación.

$Descripción: H:\Enviados 10SIII\Dibujo1_método.jpg$

Fig. 1. Proceso propuesto para obtener grupos para el aprendizaje cooperativo.

Es un método diferente al modelo MDGP clásico, porque incorpora condiciones adicionales para un mayor control en la distribución de los estudiantes a los grupos heterogéneos y utiliza una función objetivo también diferente, tal como lo han hecho otros autores de la bibliografía consultada.

1) Caracterización de los estudiantes: teniendo presente la variedad de atributos en la literatura para formar grupos de estudiantes, se utilizaron en este trabajo: a) situación académica; b) situación socioeconómica; c) disponibilidad de recursos informáticos propios y conectividad; d) actitudes para el aprendizaje.

Cada uno de estos atributos es multidimensional y algunos pueden tener componentes cualitativos, lo que dificulta su medición. Es el caso de las actitudes para el aprendizaje, para lo cual se utilizó la encuesta estandarizada sobre las actitudes respecto al pensamiento y el aprendizaje ATTLS (Attitudes Towards Thinking and Learning Survey). Con esta se obtienen indicadores que revelan si los estudiantes son candidatos a trabajar en forma colaborativa, y que tanto prefieren el aprendizaje individualizado [22], [23].

Las otras características son más sencillas de medir, utilizando escalas cuantitativas. Para cada atributo se establecieron categorías de valoración (desde una condición más favorable a una menos favorable) y para las situaciones socio-económica y académica se consideraron varias variables. Para la primera: forma de mantención (trabaja/recibe ayuda de padres o familiares/becas/otras); horas dedicadas a trabajar; número de personas a cargo, entre otras; para la segunda: promedio académico, número de materias aprobadas por año, resultado de una evaluación diagnóstico inicial, entre otras. La disponibilidad de recursos informáticos propios se consideró importante, porque en el curso donde se aplicó se combinan las modalidades de trabajo presencial y virtual [24].

2) Identificación de subconjuntos homogéneos: en este paso se utilizó la técnica análisis clúster, que permite asignar individuos a grupos (clústeres), de manera que los individuos en un mismo clúster sean más similares entre sí y entre diferentes clústeres resulten disímiles [9], [25]. Se siguieron los procedimientos que presentan Winston y Albright [25] para modelar y optimizar en hojas de cálculo.

3) Distribución en grupos heterogéneos: el último paso consiste en repartir desde los subconjuntos homogéneos a los grupos heterogéneos, pero balanceados entre sí. Para esto se elaboró un modelo matemático, cuya formulación es:

Minimizar:

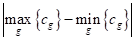
(7)

Sujeta a:

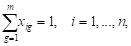
	(8)
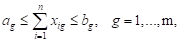
	(9)
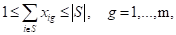
	(10)
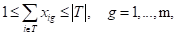
	(11)
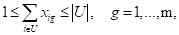
	(12)
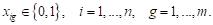
	(13)

Donde c_ges unamedida de la situación favorable/desfavorable de cada grupo, considerando z_k atributos estandarizados, con k=1,…,t :

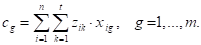
(14)

La variable x_ig es binaria, toma valor 1 si el i-ésimo estudiante forma parte del g-ésimo grupo y 0 en otro caso, con i=1,…., n y g=1,…, m. La función objetivo (7) busca minimizar las diferencias entre los grupos más favorecido y menos favorecido, para obtener así el balance entre ellos. Las restricciones (8) y (9) provienen del modelo MDGP original (2 ‒ 4). Los subconjuntos S y T en (10) y (11) corresponden a subgrupos homogéneos obtenidos en el paso anterior, con atributos más favorables y menos favorables respectivamente. Por ejemplo, S podría estar formado por estudiantes con: situaciones académica y socio-económica favorables, con recursos informáticos propios, ATTLS-1: alto, ATTLS-2: bajo; mientras que T podría ser lo contrario. Así, (10) y (11) tratan de lograr una repartición equitativa. La restricción (2) permite asignar estudiantes de un subconjunto U, con alguna característica específica (ejemplo: género), de manera equilibrada.

El modelo se implementó en hoja de cálculo. Por las características del modelo, como método de solución se aplicó algoritmo genético, incorporado en el complemento optimizador de la hoja de cálculo. Para su configuración (población, mutación, tiempo máximo sin mejora) se siguieron las propuestas de Winston [26].

El método propuesto se utilizó por primera vez sobre un conjunto de 18 estudiantes que cursaron una asignatura en la carrera de Ingeniería Industrial en la FIUNaM. El objetivo fue formar grupos de entre 4 a 5 estudiantes, para realizar actividades bajo esta modalidad durante la segunda mitad del curso.

Con análisis clúster se identificaron 6 grupos homogéneos, que incluían 4 perfiles de situación académica (favorable; favorable-medio; desfavorable-medio; desfavorable) y 3 tipos de situación socio-económica (favorable; medio; desfavorable). Con la encuesta ATTLS se identificaron 2 perfiles de actitudes para el aprendizaje.

Con el modelo matemático para la distribución en grupos heterogéneos se obtuvieron 4 grupos. A modo de ejemplo, en la Tabla 1 se representa un grupo (se omitieron identidades).

Tabla 1. Un grupo obtenido mediante el procedimiento desarrollado.

Estudiante	Situación académica	Situación socioeconómica	Recursos informáticos	ATTLS-1		ATTLS-2		Género
X₁	Favorable-medio	Desfavorable	Si	Bajo	Medio		1
X₂	Favorable-medio	Medio	Si	Medio	Medio		2
X₃	Desfavorable-medio	Favorable	No	Alto	Medio		1
X₄	Favorable-medio	Favorable	Si	Medio	Medio		2
X₅	Favorable	Favorable	Si	Medio	Medio		2

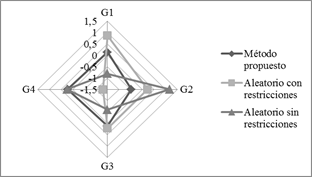
Se compararon los resultados del procedimiento propuesto con otros métodos comúnmente utilizados: a) distribución aleatoria con restricciones (en este caso tratar de lograr una repartición equitativa según el género de los integrantes, además de las cantidades mínima y máxima por grupo); b) distribución aleatoria sin restricciones (salvo las de cantidades mínima y máxima por grupo). En la Fig. 2 se presenta un diagrama que compara los valores de c_g (medida de situación favorable/desfavorable de cada grupo) de los tres métodos. Se observa que, si bien el método propuesto no arroja grupos perfectamente equilibrados, resultan con menores diferencias entre sí respecto a los que se obtuvieron por métodos aleatorios.

Fig. 2. Comparación de valores c_g obtenido con el método propuesto vs. métodos aleatorios.

Se analizaron también las composiciones internas de los grupos, verificando las características deseadas de heterogeneidad intra-grupal y homogeneidad inter-grupal. Para esto se observaron y compararon la media y la varianza de los atributos estandarizados z_,para cada uno de los grupos. Estos valores se presentan en la Tabla 2. Se observa en esta tabla que con el método propuesto se obtuvieron grupos más similares entre sí

Tabla 2. Valores medios y varianzas de los atributos estandarizados z en cada grupo, obtenidos con el método propuesto y con métodos aleatorios.

	G1	G2	G3	G4
	*Método propuesto*
Media	0,033	-0,096	0,025	0,055
Varianza	0,083	0,660	0,066	0,348
	*Aleatorio con restricciones*
Media	0,217	0,043	0,043	-0,325
Varianza	0,142	0,063	0,280	0,613
	*Aleatorio sin restricciones*
Media	-0,205	0,294	-0,119	0,048
Varianza	0,004	0,001	0,670	0,244

Por último, se evaluó la equivalencia entre los grupos obtenidos. Para esto, se realizó una prueba de Kruskal-Wallis (test-H) para determinar si los atributos de los estudiantes entre cada grupo difieren significativamente entre sí [20], [27], [28]. Como hipótesis nula se definió que no existen diferencias entre los grupos (H₀: H₁= H₂=H₃=H₄) y la alternativa: existen diferencias entre los grupos, de al menos uno respecto a los demás. Se obtuvo un valor H crítico mayor al estadístico H calculado con la muestra (H₍₃₎= 7,291; H= -33,680; p< 0,05), por lo que no se pudo rechazar la hipótesis nula, no encontrándose evidencia significativa de diferencias entre los grupos.

El método propuesto se implementó y se obtuvieron buenos resultados, quedando como actividad futura evaluar el impacto de la formación de los grupos en el desempeño de los estudiantes.

4. Conclusiones

Para formar la competencia de trabajo en equipo, puede aplicarse la estrategia de trabajo en grupos cooperativos, de tal forma que los estudiantes trabajen solidariamente y aprendan conjuntamente. Pero para alcanzar un aprendizaje cooperativo eficaz se requiere que los grupos estén adecuadamente diseñados, debiéndose constituir grupos de tamaño reducido, preferentemente heterogéneos.

La importancia del diseño de los grupos justifica que se utilicen métodos más eficientes que la distribución aleatoria. Existen modelos matemáticos que pueden aplicarse, aunque muchos de ellos por su naturaleza combinatoria proveen soluciones aproximadas.

El procedimiento propuesto e implementado en una asignatura dentro del MFPC en la FIUNaM, proporciona grupos especialmente constituidos para el aprendizaje cooperativo. Los resultados muestran que los grupos formados con este método se ajustan mejor a las características deseadas, que los que se obtienen por métodos aleatorios, que son lo que se utilizan en forma habitual.

Referencias

[1]	Consejo Federal de Decanos de Ingeniería de Argentina – CONFEDI, Competencias y perfil del ingeniero iberoamericano, formación de profesores y desarrollo tecnológico e innovación (Documentos Plan Estratégico ASIBEI), ARFO Editores e Impresores, Bogotá, 2016.
[2]	Aldag, R. J., Kuzuhara, L. W, Creating high performance teams: applied strategies and tools for managers and team members, Routledge, New York- London, 2015.
[3]	Kowalski, V. A., Erck, M. I., Enriquez, H. D., “Avances en un modelo de formación por competencias en investigación operativa para ingenieros/as industriales”, XXIX Encuentro Nacional de Docentes en Investigación Operativa y XXVII Escuela de Perfeccionamiento en Investigación Operativa, pp. 1-20, Buenos Aires, Jun. 2016.
[4]	Kowalski, V. A., Erck, M. I., Enriquez, H. D., “Formación por competencias en ingeniería industrial: moda o mejora académica?”, III Congresso Internacional de Educação Científica e Tecnológica CIECITEC, pp. 1-10. Santo Ângelo, Jun. 2015.
[5]	De Miguel Díaz, M. (Dir), Modalidades de enseñanza centradas en el desarrollo de competencias: orientaciones para promover el cambio metodológico en el espacio europeo de educación superior, Ediciones de la Universidad de Oviedo, Oviedo, 2006.
[6]	West, M. A., Effective teamwork: practical lessons from organizational research, John Wiley & Sons, 3a ed., Chichester, 2012
[7]	Pang, Y., Mugno, R., Xue, X., Wang, H., “Constructing collaborative learning groups with maximum diversity requirements”, 2015 IEEE 15^th International Conference on Advanced Learning Technologies, pp. 34-38. Hualien, Jul. 2015.
[8]	Tröster, C., Mehra A., van Knippenberg, D., “Structuring for team success: the interactive effects of network structure and cultural diversity on team potency and performance”, Organizational Behavior and Human Decision Processes, vol. 124, nº 2, pp. 245-255, Jul. 2014.
[9]	Ounnas, A., “Enhancing the automation of forming groups for education with semantics”, Tesis doctoral, School of Electronics and Computer Science, University of Southampton, Southampton, Nov. 2010.
[10]	Johnson, D. W., Johnson, F. P., Joining together: group theory and group skills, Pearson Education, 11a ed., Harlow, 2014.
[11]	Slavin, R. E., Educational psychology: theory and practice, Pearson Education, 8a ed., Boston, 2006.
[12]	Yeoh, H. K., Mohamad Nor, M. I., “An algorithm to form balanced and diverse groups of students”, Computer Applications in Engineering Education, vol. 19, nº 3, pp.582-590, Sep. 2011.
[13]	Cohen, E. G., Lotan, R. A., Designing groupwork: strategies for the heterogeneous classroom, Teachers College Press, 3a ed., New York, 2014.
[14]	Pinninghoff J., M. A., Ramírez, M., Contreras A., R., Salcedo L., P., “Collaborative group formation using genetic algorithms”, 6^th International Work-Conference on the Interplay Between Natural and Artificial Computation IWINAC2015, pp. 1-10, Elche, Jun. 2015.
[15]	Sadeghi, H., Kardan, A. A., “A novel justice-based linear model for optimal learner group formation in computer-supported collaborative learning environments”, Computers in Human Behavior, vol.48, pp. 436-447, Jul. 2015.
[16]	Gallego, M., Laguna, M., Martí, R., Duarte, A., “Tabu search with strategic oscillation for the maximally diverse grouping problem”, Journal of the Operational Research Society, vol. 64, nº 5, pp. 724-734, 2013.
[17]	Rodriguez, F. J., Lozano, M., García-Martínez, C., González-Barrera, J. D., “An artificial bee colony algorithm for the maximally diverse grouping problem”, Information Sciences, vol. 230, pp. 183-196, May. 2013.
[18]	Brimberg, J., Mladenović, N., Urošević, D., “Solving the maximally diverse grouping problem by skewed general variable neighborhood search”, Information Sciences, vol. 295, pp. 650-675, Feb. 2015.
[19]	Baker, K. R., Powell, S. G., “Methods for assigning students to groups: a study of alternative objective functions”, Journal of the Operarional Research Society, vol. 53, nº 4, pp. 397-404. Abr. 2002.
[20]	Mertens, D. M., Research and evaluation in education and psychology: integrating diversity with quantitative, qualitative, and mixed methods, SAGE Publications, 3a ed., California- London- New Delhi- Singapore, 2010.
[21]	Hernández Sampieri, R., Fernández Collado, C., Baptista Lucio, M., Metodología de la investigación, McGraw-Hill, 6a ed., México, 2014.
[22]	Marín García, M. P., Astruc, L., “Motivating students through technology: using media and collaborative technologies in language teaching and learning”, 6th International Technology, Education and Development Conference INTED2012, pp. 1594 -1603, Valencia, Mar. 2012.
[23]	Cuevas Valencia, R. E., Morales, A. F., Bonilla Silva, P., Espinosa Organista, J., “Aprendizaje combinado: encuesta de actitudes hacia el pensamiento y el aprendizaje”. National and International Research Articles CIEX Journal, nº1, pp. 47-57, Ene/Jun. 2015.
[24]	Kowalski, V. A., Erck, I. M., Enriquez, H. D., “Potencialidades del blended learning para la formación por competencias de ingenieros industriales”, VII Congreso Virtual Iberoamericano de Calidad en Educación Virtual y a Distancia Eduq@2017, pp. 1-17, 2017.
[25]	Albright, S. C., Winston, W. L., Business analytics: data analysis and decision making, Cengage Learning, 5a ed., Stamford, 2015.
[26]	Winston, W. L., Microsoft Excel 2016 data analysis and business modelling, Microsoft Press, Redmond, 2016
[27]	Cohen, L., Manion, L., Morrison, K., Research methods in education, Routledge, 6a ed., Oxon, 2007.
[28]	Corder, G. W., Foreman, D. I., Nonparametric statistics: a step-by-step approach, John Wiley & Sons, 2a ed., Hoboken, 2014.